Выбор конкурентоспособного товара методом нечеткого отношения предпочтения

Оценка эффективности ГС различными методами.

Бурение горизонтальных скважин.

Метод ИНФП.

Оценка технологического эффекта импульсного воздействия.

Гидродинамический и капиллярный эффект импульсного воздействия.

Физические основы импульсного воздействия на пласт.

Совершенствование технологий разработки нефтяных месторождений.

ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПОДГОТОВКИ

Под конкурентоспособностью понимают комплекс потребитель­ских, стоимостных и социальных характеристик товара (изделия), определяющих его успех на данном рынке, т. е. способность дан­ного товара быть обмененным на деньги на конкретном рынке в условиях широкого предложения к обмену других конкурирую­щих товаров-аналогов. Конкурентоспособность — это степень соответствия совокупности свойств объекта ценностной системе рынка. Границы понятия конкурентоспособность непрерывно рас­ширяются, переходя от конкурентоспособности изделия к конку­рентоспособности предприятий и даже государств. Конкуренто­способность обеспечивается высоким технологическим уровнем и качеством, соответствием требованиям и стандартам стран-им­портеров, фирм-покупателей, высоким уровнем технологического обслуживания, патентной чистотой и патентной защитой, прием­лемой ценой, льготными условиями платежа и т. д.

Проанализируем ряд виброзащитных технологий для выявле­ния наиболее конкурентоспособной на определенном международ­ном рынке.

Защита современных транспортных систем, в частности автомо­билей, от механических динамических воздействий обеспечивается виброизоляторами. Виброизоляторы являются комплектующими эле­ментами, которые закупаются на рынке фирмами — производителя­ми автомобилей. Разновидностей виброизоляторов достаточно мно­го. Поэтому перед фирмами изготовителями, с одной стороны, и фирмами-покупателями — с другой, возникает проблема выбора наи­более рациональных элементов для производства и эксплуатации.

Задачу выбора рационального виброизолятора с учетом наибо­лее важных критериев качества рассмотрим на примере анализа четырех альтернатив: а1 — пневматического виброизолятора; a2 — металлического торсионного элемента, работающего на скру­чивание; a3 — винтовой пружины; a4 — резинового элемента.

Для оценки альтернатив используем восемь критериев качества:

F1 — собственная частота колебаний виброизолятора (f, Гц);

F2—долговечность элемента (Т, лет);

F3 — габаритный размер (h, метр);

F4 — коэффициент передачи на резонансе (Tz, безразмерные единицы);

F5 — устойчивость к механическим повреждениям (шкала эк­спертных оценок);

F6 — стоимость (тыс. руб.);

F7 — шумоизоляция (дБ);

F8 — патентная чистота (условные единицы измерения).

На основании функций принадлежности всех альтернатив по восьми критериям определены их конкретные значения, которые представляют собой следующие нечеткие множества:

По этим данным составлены матрицы нечетких отношений предпочтения R1,..., R8

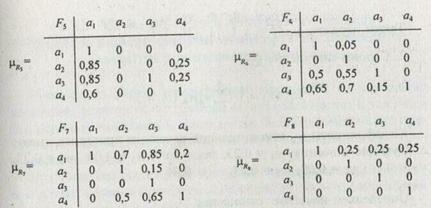
Задача выбора решается в соответствии с описанной выше про­цедурой.

1. Строим нечеткое отношение Q1 = R1 Ç R2 Ç …Ç R8:

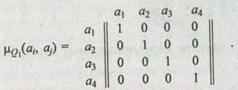
Находим подмножество недоминируемых альтернатив на мно­жестве А

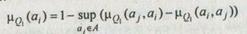
по всем i и j (i ¹ j):

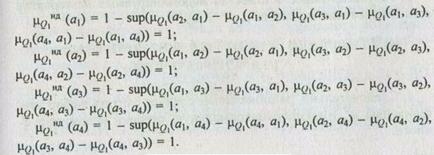
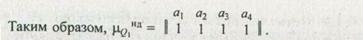
2. Строим отношение Q2.

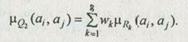
Коэффициенты wk относительной важности критериев имеют следующие значения: w1 = 0,23, w2 = 0,09, w3 = 0,04, w4 = 0 23 w5 = 0,04, w6 = 0,09, w7 = 0,23, w8 = 0,04.

Определяем нечеткое отношение Q2.

Находим подмножество недоминируемых альтернатив множе­ства А,

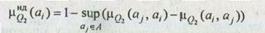
по всем i и j (i ¹ j):

3. Результирующее множество недоминируемых альтернатив есть пересечение множеств

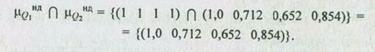
4. Следовательно, рациональным следует считать выбор аль­тернативы a1 имеющей максимальную степень недоминируемости.

. 3. Метод нечеткого логического вывода в задаче выбора фирмой кандидата на замещение вакантной должности бухгалтера

Руководство фирмы рассматривает кандидатов на замещение вакантной должности бухгалтера. Задача заключается в том, что­бы, используя описанный выше метод, выявить наилучшего пре­тендента. Обсуждение среди членов руководства фирмы дало сле­дующий результат:

d1: "Если кандидат имеет требуемые квалификацию, образова­ние и опыт ведения бухгалтерского учета, то он — удовлетворяю­щий (отвечающий требованиям)";

d2: "Если он вдобавок к вышеописанным требованиям умеет работать с современным программным обеспечением (ПО), то он — более чем удовлетворяющий";

d3: "Если он дополнительно к условиям d2 обладает необходи­мыми юридическими знаниями, то он — безупречный";

d4: "Если он имеет все оговоренное в d3, кроме способности работать с современным ПО, то он — очень удовлетворяющий";

d5: "Если кандидат имеет необходимую квалификацию, имеет опыт ведения бухгалтерского учета, обладает юридическими зна­ниями, но не имеет высшего образования, он все же будет удов­летворяющим";

d6: "Если он не имеет квалификации и не имеет опыта ведения бухгалтерского учета, то он — неудовлетворяющий".

Анализ приведенных информационных фрагментов позволяет выявить шесть критериев, используемых для принятия решения:

Х1 — квалификация; Х2 — образование; Х3, — опыт ведения бухгалтерского учета; Х4, — умение работать с современным ПО; Х5 — юридическая грамотность, Y— удовлетворительность.

Для формулирования правил следует определить возможные значения лингвистических переменных Xi и Y, которые будут ис­пользоваться для оценки кандидатов:

d1: "Если Х1 = ПОДХОДЯЩЯЯ и X2 = ВЫСШЕЕ, и Х3 = ДО­СТАТОЧНЫЙ. то Y = УДОВЛЕТВОРЯЮЩИЙ";

d2: "Если Х1 = ПОДХОДЯЩАЯ и X2 = ВЫСШЕЕ, и Х3 = ДО­СТАТОЧНЫЙ, и X4 = СПОСОБЕН, то Y = БОЛЕЕ ЧЕМ УДОВ­ЛЕТВОРЯЮЩИЙ";

d3: "Если Х1 = ПОДХОДЯЩАЯ и Х2 = ВЫСШЕЕ, и X3 = ДО­СТАТОЧНЫЙ, и Х4 = СПОСОБЕН, и X5 = ОБЛАДАЕТ, то Y = БЕЗУПРЕЧНЫЙ";

d4: "Если Х1 = ПОДХОДЯЩАЯ и Х2 = ВЫСШЕЕ, и Х3 = ДО­СТАТОЧНЫЙ, и X4 = ОБЛАДАЕТ, то Y = ОЧЕНЬ УДОВЛЕТВО­РЯЮЩИЙ";

d5: "Если Х1 = ПОДХОДЯЩАЯ и X2 = НЕ ВЫСШЕЕ, и Х3 = ДОСТАТОЧНЫЙ, и X5 = ОБЛАДАЕТ, то Y = УДОВЛЕТВОРЯЮ­ЩИЙ";

d6: "Если Х1 = НЕ ИМЕЕТ и Х3 = НЕДОСТАТОЧНЫЙ, то Y = НЕУДОВЛЕТВОРЯЮЩИЙ".

Переменная Y задана на множестве J = {0; 0,1; 0,2;...; 1}.

Значения переменной Y заданы с помощью следующих функ­ций принадлежности:

S = УДОВЛЕТВОРЯЮЩИЙ определено как mS(х) = х, х Î J;

MS = БОЛЕЕ ЧЕМ УДОВЛЕТВОРЯЮЩИЙ — как mMS(x)=Öx; x Î J;

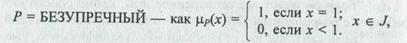
VS = ОЧЕНЬ УДОВЛЕТВОРЯЮЩИЙ — как mVS(x) = х2, x Î J,

US = НЕУДОВЛЕТВОРЯЮЩИЙ — как mVS(x) = 1 - х, х Î J.

Выбор производится из пяти кандидатов на множестве U = {u1, и2, u3, u4, u5}.

В рассматриваемой задаче оценки кандидатов заданы следую­щими нечеткими множествами:

ПОДХОДЯЩАЯ (квалификация) А = {0,8/u1, 0,61u2, 0,5/u3, 0,1/u4, 0,3/u5};

ВЫСШЕЕ (образование) В = {0,5/u1,1/u2, 0/u3, 0,5/u4, 1/u5};

ДОСТАТОЧНЫЙ (опыт) С = {0,6/u1, 0,9/и2, 1/u3, 0,7/u4, 1/u5};

СПОСОБЕН (работать с ПО) D = {1/u1, 0,3/и2, 1/u3, 0/u4, 0/u5}',

ОБЛАДАЕТ (юридическими знаниями) Е = {0/u­1, 0,5/u2, 1/u3, 0,8/u4, 1/u5}.

С учетом введенных обозначений правила d1,...,d6 принимают вид:

d1: “Если Х= А и В, и С, то Y =S”;

d2: "Если Х= А и В, и С, и D, то Y = MS":

d3: “Если X= А и В, и С, и D, и E, то Y = P”;

d4: “Если X = А и B, и С, и Е, то Y = VS”;

d5: “Если X = A, и не В, и С, и E, то Y = S”;

d6: “Если Х = не A и не С, то Y = US”.

Вычислим функции принадлежности

для левых частей при­веденных правил:

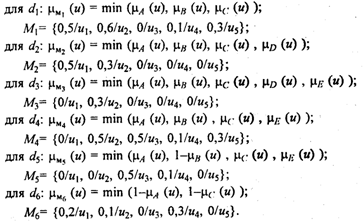
Теперь правила можно записать в виде:

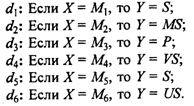
Используя для преобразования правил вида "Если Х = М, то Y = Q" импликацию Лукасевича mD(u, j) = min(l, 1-mM /(u) + mY (j)), для каждой пары (u, j) Î U х J получаем следующие не­четкие отношения на U ´ J:

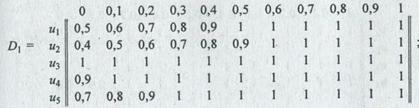
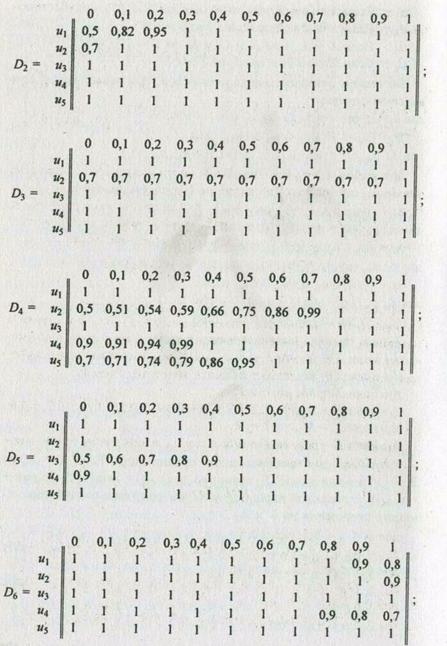
В результате пересечения отношений D1,..., D6 получаем об­щее функциональное решение:

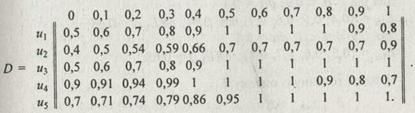
Для вычисления удовлетворительности каждой из альтернатив применим правило композиционного вывода в нечеткой среде:

Ek = Gk ° D, где Еk — степень удовлетворения альтернативы k;

Gk — отображение альтернативы k в виде нечеткого подмноже­ства на U, D — общее функциональное решение. Тогда

Для первой альтернативы

E1 ={0,5/0; 0,6/0,1; 0,7/0,2; 0,8/0,3; 0,9/0,4; 1/0,5; 1/0,6; 1/0,7; 1/0,8; 0,9/0,9; 0,8/1}.

Вычисляем уровневые множества Eja и мощность такого мно­жества М(Еa) по формуле

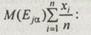
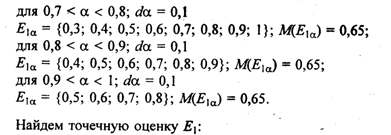
Аналогично находим точечные оценки для других альтернатив:

для второй альтернативы F(E2) = 0,656;

для третьей — F(E3) = 0,575;

для четвертой — F(E4) = 0,483;

для пятой — F(E5) = 0,562.

В качестве лучшей выбираем альтернативу, имеющую наиболь­шую точечную оценку. В нашем примере это альтернатива и2, следовательно, она и будет наилучшей. Второе место занимает аль­тернатива u3; третье – u5, четвертое – и1, а самой худшей из аль­тернатив является u4.

Дата добавления: 2014-01-07