Действия с комплексными числами

Сумма, разность, произведение, частное комплексных чисел, сопряжённых с исходными, есть комплексное число, сопряжённое с суммой, разностью, произведением, частным исходных комплексных чисел.

Во многих случаях удобнее пользоваться тригонометрической формой комплексного числа. Переход от алгебраической формы комплексного числа к тригонометрической осуществляется на основе простейших формул тригонометрии (см. рисунок).

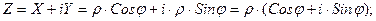
Здесь: - модуль комплексного числа;

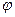- аргумент – угол, который отсчитывается от действительной оси ОХ в направлении против часовой стрелки (в положительном направлении).

Комплексное число в тригонометрической форме приобретает свойство периодичности. .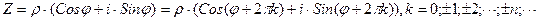

Такие математические операции над комплексными числами, как умножение, деление, возведение в степень и извлечение корня удобнее осуществлять, используя тригонометрическую форму комплексных чисел

Пусть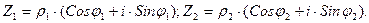

1).

2).

Сформулируем полученное правило.

При перемножении комплексных чисел их модули - перемножаются, а аргументы – складываются. При делении – их модули делятся, а аргументы – вычитаются.

3). Используя формулу 1, запишем формулу для возведения в степень.

(формула Муавра).

4). Извлечение корня из комплексного числа осуществляется по следующему правилу.

Доказательство.

Пусть 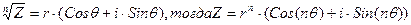(формула Муавра).

Но два комплексных числа в тригонометрической форме равны тогда, когда их модули равны, а аргументы отличаются на число, кратное .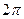

Отсюда получим:

Таким образом при извлечении корня из комплексного числа имеем столько корней, какова степень корня.

В теоретических основах электротехники широко используется показательная форма комплексного числа. Переход от тригонометрической формы к показательной осуществляется при помощи формул Эйлера.

Используя эти формулы, получим:

Правила умножения, деления, возведения в степень и извлечения корня из комплексного числа в показательной форме аналогичны правилам для комплексных чисел в тригонометрической форме.

Если то используют формулы.

1).

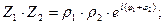
2).

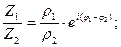
3).

4).

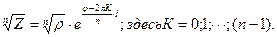
Дата добавления: 2014-01-07