Обыкновенные дифференциальные уравнения 1-го порядка

Обыкновенным дифференциальным уравнением 1-го порядка называется уравнение, связывающее независимую переменную, неизвестную искомую функцию, зависящую от этой переменной, и ее производную 1-го порядка.

В неявной форме записи дифференциальное уравнение 1-го порядка выглядит следующим образом: 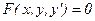, (3)

где F – известная функция своих аргументов;

х – независимая переменная;

у – искомая неизвестная функция, зависящая от х;

или (в разрешенном относительно у^/ виде): 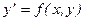, (4)

где f – известная функция своих аргументов.

Заметим, что функция F в уравнении (3) может не содержать х или у (или оба этих аргумента), но непременно должна включать у^/.

Дифференциальное уравнение 1-го порядка имеет бесчисленное множество решений. Так, например, решением уравнения 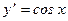будет являться не только функция 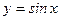, но и всякая функция вида 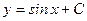(где С – произвольная постоянная), в чем можно убедиться непосредственной проверкой.

Одной из важных задач теории дифференциальных уравнений является задача Коши (Коши Огюстен Луи (1789-1857) – французский математик).

Для уравнения (4) (или (3)) задача Коши формулируется следующим образом: «среди всевозможных решений указанного уравнения найти такие, которые удовлетворяют заданному условию: 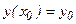, (5)

где х₀, у₀ – заданные действительные числа»

Условие (5) называется начальным условием.

Геометрическая интерпретация задачи Коши заключается в следующем: среди всех интегральных кривых уравнения (4) (или (3)) найти такие, которые проходят через наперед заданную точку с координатами (х₀, у₀) плоскости Оху.

Общим решением дифференциального уравнения 1-го порядка называется однопараметрическое семейство функций: 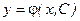, (6)

удовлетворяющее следующим условиям:

а) функция (6) является решением данного дифференциального уравнения при любом допустимом значении параметра С;

б) при любом допустимом начальном условии 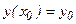найдется такое значение С₀ параметра С, при котором функция 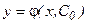будет удовлетворять указанному начальному условию, т.е. будет иметь место равенство: .

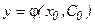Всякое решение 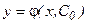дифференциального уравнения 1-го порядка, которое получается из общего решения (6) при конкретном, и вполне определенном значении С = С₀, называется частным решением.

Таким образом, общему решению (6) дифференциального уравнения 1-го порядка на плоскости Оху соответствует семейству интегральных кривых; а частному решению, удовлетворяющую начальному условию 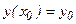- кривая этого семейства 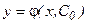, проходящая через точку .

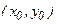Общее решение дифференциального уравнения 1-го порядка, выраженное в неявной форме, т.е. в виде 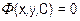, называется общим интегралом.

Дифференциальные уравнения с разделяющимися переменными.

Простейшими дифференциальными уравнениями 1-го порядка являются дифференциальные уравнения с разделяющимися переменными.

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: (7)

(или приводящееся к указанному виду).

Характерной особенностью уравнения (7) является то, что коэффициенты при дифференциалах dx, dy представляют собой произведение функций, зависящих только от х, или только от у.

Преобразуем дифференциальное уравнение (7) таким образом, чтобы при dx множителем была функция, зависящая только от х, а при dy – функция, зависящая только от у. С этой целью разделим обе части уравнения (7) на функцию 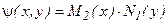(предполагая, что 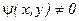, в результате чего получаем:

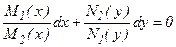(8)

При этом могли быть потеряны решения уравнения (7), которые одновременно являются и решениями уравнениями 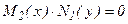. Эти решения записываются в ответ в том случае, если их нельзя будет получить из общего решения ни при каком конкретном значении параметра С.

Почленное интегрирование уравнения (8) приводит к соотношению:

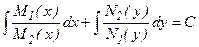, (9)

(где С – произвольная постоянная, всегда возникающая при применении операции неопределенного интегрирования), которое и определяет общее решение исходного уравнения (7) в неявной форме (общий интеграл).

Пример 2. Для дифференциального уравнения 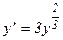найти:

1) все его решения;

2) частное решение, удовлетворяющее условию .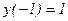

Решение. 1) Заданное уравнение представляет собой дифференциальное уравнение 1-го порядка с разделяющимися переменными. Запишем его в виде:

.

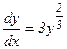Умножив обе части этого уравнения на dx, получаем: .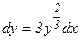

Разделив обе части последнего уравнения на 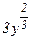(предполагая, что 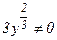), имеем:

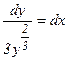(10)

Проинтегрируем обе части уравнения (10): ;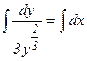

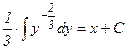, где С =сonst;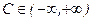

;

;

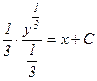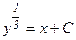Откуда 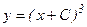(11)

Итак, соотношение (11) определяет общее решение исходного уравнения. В процессе перехода к уравнению (10) при делении на функцию 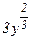, могло быть потеряно решение заданного уравнения, которое одновременно является и решением уравнения 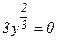, т.е. у = 0. Непосредственной проверкой убеждаемся, что функция у = 0 действительно является решением заданного уравнения (так как, если у = 0, то у^/ = 0 и при их подстановки в исходное уравнение 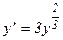, получается тождество 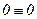). Однако, решение у = 0 невозможно получить из общего решения (11) ни при каком числовом значении параметра С, следовательно, оно утрачено.

Таким образом, совокупность всех решений заданного уравнения имеет вид:

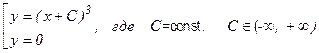
2) Чтобы найти частное исходного уравнения, удовлетворяющее начальному условию у (-1) = 1, подставим х₀ = -1 и у₀ = 1 в общее решение (11):

1 = (-1 + С)^-3;

(С – 1)³ = 1;

С – 1 = 1;

С = 2.

Подставив полученное выше значение параметра С в общее решение (11), находим частное решение, удовлетворяющее заданному начальному условию: у = (х +2)³.

С геометрической точки зрения, мы нашли ту интегральную кривую (кубическую параболу), которая на плоскости Оху проходит через точку М₀ (-1; 1) (рис. 1).

Общему решению (11) на плоскости Оху соответствует семейство кубических парабол, смещающихся вдоль оси ОХ при изменении постоянной интегрирования С.

При С = 0 из (11) имеем: у = х³

С = 1 у = (х + 1)³;

С = 2 у = (х + 2)³;

С = 3 у = (х + 3)³;

С = -1 у = (х - 1)³;

С = -2,5 у = (х – 2,5)³.

Пример 3. Решить дифференциальное уравнение: у² – 4 – 2хуу^/ = 0 (12)

Решение. Уравнение (12) представляет собой дифференциальное уравнение с разделяющимися переменными. Запишем его в виде:

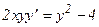, откуда .

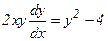Умножив обе части последнего уравнения на dx, получим:

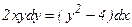(13)

Преобразуем уравнение (13) таким образом, чтобы множителем при dx являлась функция, зависящая только от х, а при dy – функция, зависящая только от у. С этой целью, разделив обе части уравнения (13) на 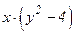, будем иметь:

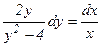(14)

Проинтегрируем обе части равенства (14). Имея в виду дальнейшие преобразования, обозначим произвольную постоянную через 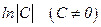, что допустимо, так как, если С – константа, то и 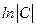- тоже константа, принимающая любое значение от 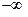до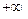

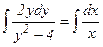
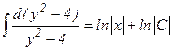, где С – const; С ≠ 0

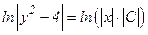
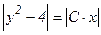
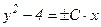
Положим С₀ = ± С (где С₀ = const, причем 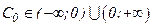), тогда

;

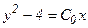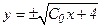, где С₀ = const; С ≠ 0 (15)

Таким образом, функция (15) определяет общее решение заданного уравнения (12).

В процессе преобразований при переходе от уравнения (13) к уравнению (14) могли быть потеряны решения заданного уравнения (12), которые одновременно являются и решениями уравнения 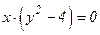(т.е. х = 0, у = 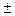2)

Непосредственной проверкой убеждаемся, что х = 0 не является решением уравнения (12), а у = ± 2 являются его решениями (действительно при подстановке у = ± 2 в уравнение (12) получаем тождество ).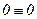

Заметим, что решение у = ± 2 можно получить из общего решения (15), если допустить, что постоянна С₀ в (15) может принимать значение равное нулю (т.е. С₀ = 0).

Таким образом, все решения исходного уравнения (12) определяется формулой (15), в которой постоянная .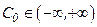

Ответ: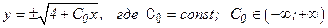

Дата добавления: 2014-01-07