Основные понятия. Дифференциальные уравнения высших порядков

Дифференциальные уравнения высших порядков.

Дифференциальные уравнения высших порядков имеют большое значение в прикладных задачах. Так, например уравнения 2-го порядка – в теории колебаний, теории электрических цепей, в задачах механики.

Согласно данному в лекции 1 определению, самый общий вид обыкновенного дифференциального уравнения n – го порядка (n ≥ 2) следующий:

, (41)

где F – известная функция своих аргументов;

х – независимая переменная;

у – неизвестная искомая функция, зависящая от х.

В данном курсе ограничимся рассмотрением уравнений n – го порядка, разрешенных относительно старшей производной, т.е. имеющих вид:

, (42)

где f – известная функция своих аргументов.

Решением дифференциального уравнения (42) (или (41)) называется всякая n – раз дифференцируемая функция , которая обращает указанное уравнение в тождество (лекция 1, пример 1).

Задача Коши для дифференциального уравнения n – го порядка (n ≥ 2) состоит в том, чтобы найти решение этого уравнения, удовлетворяющее условиям:

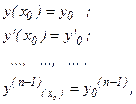(43)

где - заданные действительные числа.

Условия (43) называются начальными условиями.

Для дифференциального уравнения 2-го порядка начальные условия (43) имеют вид: ;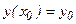

,

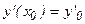а геометрическая интерпретация задачи Коши заключается в следующем: среди интегральных кривых отыскать такие, которые проходят через точку М₀ (х₀, у₀) плоскости Оху и имеют в этой точке касательную с угловым коэффициентом k равным у^/₀ (т.е. k = у^/₀).

Общим решением дифференциального уравнения n – го порядка называется n – параметрическое семейство функций:

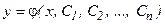, (44)

удовлетворяющее следующим условиям:

а) при подстановке функции (44) в уравнение последнее обращается в тождество относительно х при любых допустимых значениях произвольных постоянных С₁, С₂,. С_n..

б) при любых допустимых начальных условиях (43) найдутся такие значения С₁⁰, С₂⁰,. С_n⁰ постоянных С₁, С₂,. С_n, что функция 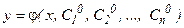будет удовлетворять этим начальным условиям.

Общее решение дифференциального уравнения (50) (или (49)), найденное неявно в виде: 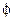(х, у, С₁, С₂,, С_n) = 0 называется общим интегралом этого уравнения.

Всякое решение 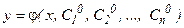, получаемое из общего решения (44) при конкретном вполне определенном наборе значений 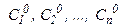постоянных , называется частным решением.

Интегрирование дифференциальных уравнений n – го порядка точным аналитическим методом (в квадратурах) удается произвести только в некоторых частных случаях, которые и рассматриваются в следующих параграфах.

Дата добавления: 2014-01-07