Совместное распределение нескольких случайных величин

Для изучения системы случайных величин надо знать закон совместного распределения их вероятностей. Рассмотрим систему 2-х случайных величин x и y, т.е. двумерную случайную величину. Систему двух случайных величин рассматриваем как систему двух одномерных величин. Каждую из величин x и y называют компонентой двумерной случайной величины. Двумерную случайную величину называют дискретной если ее компоненты дискретны.

(x; y)

(x_i; y_j) – возможные

Случайная величина представляет систему двух случайных величин ее декартовых координат. Задание закона ее совместного распределения величин x и y означает задание вероятности попадания случайной точки величины x, y в точку x_i; y_j. Вероятность Р(x=x_i; y=y_j)=P_i,j, i =1 ……n; j =1 ……..m. Эти вероятности могут быть любыми неотрицательными числами, сумма которых равна 1. Т.к. события x=x_i; y=y_j образуют полную группу. Т.е. закон распределения задан в виде таблицы с двумя входами. 1 столбец содержит все возможные значения x, а первая строка все возможные значения компоненты y, каждую вероятность P_i,j можно рассматривать как совмещение случайных событий x=x_i; y=y_j.

Пример:

y₁

y₂……….

y_m

x₁

P₁₁

P₁₂

P_1m

x₂

P₂₁

P₂₂

P_2n

x_n

P_n1

P_n2

P_nm

Две дискретные величины x, y называются независимыми, если для всех их возможных значений x_i; y_j имеет место равенство

P_i,j =Р(Х=x_i)×P(Y=y_j)

Это определение распределения и наибольшее число дискретных случайных величин.

Пример: В первом ящике 6 шаров, во вором также 6 шаров

I 1 шар с номером 1

2 шара с номером 2 Х - № из I ящика

3 шара с номером 3

II 2 шара с номером 1

3 шара с номером 2 Х - № из II ящика

1 шар с номером 3

Из каждого ящика взяли по шару, составить таблицу закона распределения системы случайных величин. Найти законы распределения составляющих.

x
P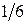

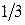
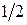
y
P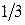

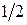
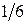
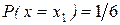
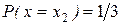
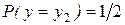
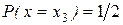
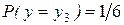
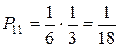
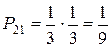
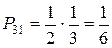
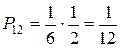
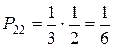
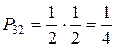
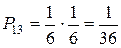
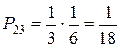
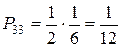
	y1	y2	y3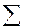
x1 x2 x3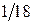

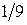
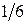
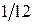
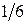
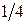
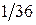
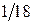
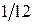
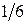
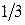
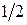
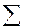
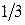
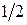
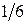
Пусть (х, у) – двумерная непрерывная случайная величина. Двумерную случайную величину (х, у) – называют непрерывной, если ее компоненты непрерывны. Кроме того величины х, у обладают непрерывной плотностью распределения.

P(x<X; y<Y)=F(x,y)

Как дифференцируемая функция

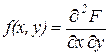
Функция удовлетворяет 2-м основным свойствам f(x,y)³ 0 и двойной интеграл

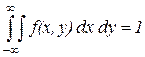
Вероятность попадания случайной точки в любую область D на плоскости х, у, может быть представлена в виде двойного интеграла:

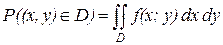
Функция распределения может быть выражена, как:

F(x;y)=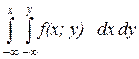

График плотности распределения называют поверхностью распределения вероятности.

Пример: Найти функцию распределения двумерной случайной величины с плотностью распределения:

f(x;y)=e^-x-y (x³0,y³0)

P(0<x<1; 0<y<2)

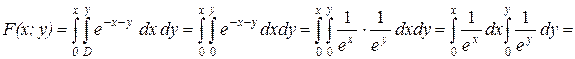
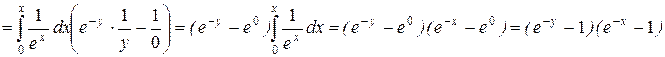
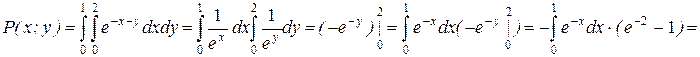
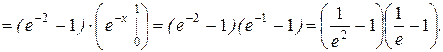
Распределение компонент непрерывной случайной величины (х; у).

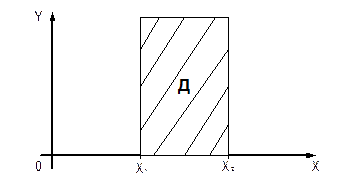Закон совместного распределения величин х и у полностью определяет законы распределения каждой из величин х и у. Пусть F(x;y) – плотность совместного распределения величин х и у. Найдем плотность распределения величины х. Рассмотрим вероятность попадания значения величины х в любой интервал от х ₁ до х ₂.

т.к. попадание абсциссы в интервале равносильно попаданию точки в вертикальную область D, то вероятности этих событий равны.

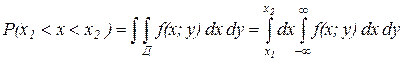
Данный интеграл можно записать и таким образом

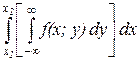
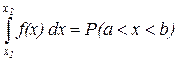
Сравним с другим равенством. Согласно определению плотности распределения следует, что искомая плотность равна

,

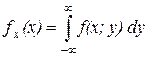Аналогично площадь распределения величины у будет равна

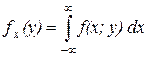
Эти понятия обобщаются для систем более 2-х величин.

Определение: Непрерывные случайные величины х и у называются независимыми, если плотность совместного распределения равна произведению плотности этих величин

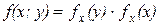-условие независимости.

Дата добавления: 2014-01-07