Представление стационарных случайных функций в виде гармонических колебаний со случайной амплитудой и случайной функцией

1. Рассмотрим случайную функцию

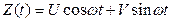, (1)

где w постоянное действительное число, U и V - некоррелированные случайные величины с математическими ожиданиями, равными нулю, и одинаковыми дисперсиями: m_u = m_v = 0, D_u = D_v = D. Преобразуем правую часть соотношения (1):

.

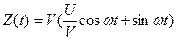Положим и выполнив элементарные выкладки, получим:

,

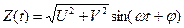где .

Отсюда следует, что случайную функцию (1) можно истолковать как гармоническое колебание со случайной амплитудой 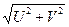, случайной фазой 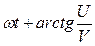и частотой w.

Заметим, что по допущенным , поэтому U и V - центрированные случайные величины: .

Легко убедится, что 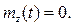Следовательно Z(t) центрированная случайная функция:

.

Покажем, что 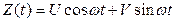- стационарная случайная функция. Действительно, 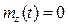, то есть постоянно при всех значениях аргумента. Найдем корреляционную функцию, приняв, что :

.

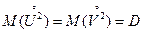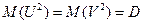Учитывая, что по условию , а так как , то . Следовательно, случайные величины U и V некоррелированы, поэтому их корреляционный момент .

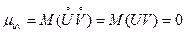Выполним элементарные выкладки, получим:

.

Итак, корреляционная функция случайная функция Z(t) зависит только разности аргументов, а ее математическое ожидание постоянно. Следовательно, Z(t) -стационарная случайная функция.

2. Рассмотрим случайную функцию X(t), которая является суммой конечного числа слагаемых вида (1):

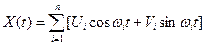(2)

где U_i и V_i не коррелированны, их математические ожидания равны нулю, дисперсии величин с одинаковыми индексами равными между собой: .

Заметим, что X(t) - центрированная функция, то есть 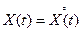. Действительно, математическое ожидание каждого слагаемого (2) равно нулю, следовательно, математическое ожидание m_x(t) этой суммы также равно 0, значит .

Докажем, что функция X(t) вида (2) - стационарная. Действительно m_x(t) = 0, при всех значениях аргумента, то есть постоянно.

Кроме того, слагаемые суммы (2) попарно не коррелированы, поэтому корреляционная функция этой суммы равна сумме корреляционных функций слагаемых. Выше доказано, что корреляционная функция каждого слагаемого (2) зависит только от разности аргументов 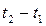. Следовательно, корреляционная функция суммы (2) также зависит только от разности аргументов:

,

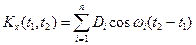или

, (3)

где .

Таким образом, случайная функция X(t) вида (2) есть стационарная функция.

Принимая во внимание, приведенное выше, что

,

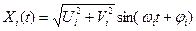где , заключаем, что сумму (2) можно представить в виде

.

Таким образом, если случайная функция X(t) может быть представлена в виде суммы гармонических различных частот со случайными амплитудами и случайными фазами, то X(t) - стационарная функция.

Дата добавления: 2014-01-07