Дроссельное регулирование скорости выходного звена гидропривода

На рис.1.6 представлена упрощенная схема исполнительного механизма гидропривода с дроссельным регулированием скорости выходного звена, состоящего из золотникового гидрораспределителя и гидроцилиндра. К гидрораспределителю подключаются магистрали от источника гидравоической энергии с постоянным давлением подачи Рп и давлением слива – Рс. К выходным отверстиям гидрораспределителя подключен силовой гидроцилиндр. Расход жидкости в первую полость гидроцилиндра Q1 и из второй полости гидроцилиндра в сливную магистраль Q2 соответственно равны:

.

В этих выражениях G1(xз) и G2(хз) – проводимости входного и выходного окон гидрораспределителя. В симметричных гидрораспределителях они практически одинаковые и определяются следующими выражениями:

.

Здесь хз – открытие окна золотника (предполагается, что в идеальных гидрораспределителях оно совпадает с перемещением золотника);

m - коэффициент расхода дросселирующего прямоугольного окна с острыми кромками.

Очевидно, что в симметричном гидрораспределителе при отсутствии утечек жидкости в статических режимах Q1=Q2. Следовательно, и

Рп-Р1=Р2-Рс =DР.

Здесь DР – перепад давления на дросселирующем окне гидрораспределителя.

Поскольку скорость поршня определяется отношением Q/Aп, то зависимость установившейся скорости поршня от перепада давления на дросселирующем (рабочем) окне гидрораспределителя может быть представлено следующим образом:

.

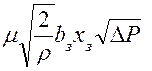Здесь bз – суммарная ширина окна гидрораспределителя. Например, если в гильзе распределителя два окна, каждое из которых равно b, то bз = 2b.

Из рассмотрения баланса суммы потерь давления на элементах гидрораспределителя и на поршне гидроцилиндра следует, что:

Здесь: - перепад давления на поршне или давление нагрузки.

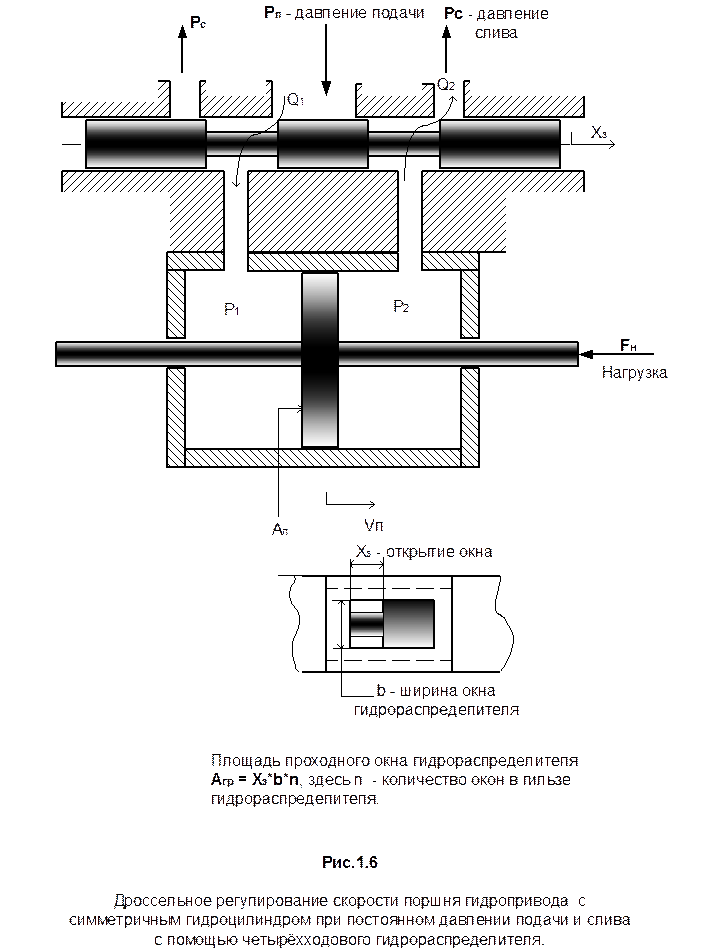
Таким образом, выражение для установившейся скорости поршня, как функции открытия рабочего окна и величины внешней нагрузки примет вид:

.

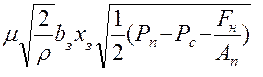Для того, чтобы сделать это выражение справедливым для идеального золотника при помогающей и противодействующей нагрузок и при смещении золотника в обе стороны от нейтрального положения, можно умножить давление нагрузки (Рн) на функцию sign(Xз). В этом случае выражение для характеристики V(Xз, Fн) примет вид:

.

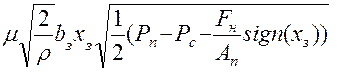Внешний вид этой характеристики для положительных значений положения золотника при противодействующей (+Fн) и отрицательной, помогающей движению поршня нагрузки (-Fн) показан на рис.1.7.

Следует отметить, что приведенное выражение справедливо только при условии .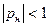

Регулировочная характеристика исполнительного механизма определяется приведенным выше выражением, но при Fн=0, т.е имеет следующий вид:

.

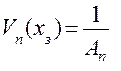
Вид регулировочной характеристики исполнительного механизма с идеальным гидрораспределителем показан на рис.1.8 толстой сплошной линией. На этом же рисунке показаны тонкими линиями регулировочные характеристики исполнительного механизма с гидрораспределителем, в котором имеются некоторые начальные перекрытия рабочих окон, которые приводят к появлению зоны нечувствительности привода, и с начальным открытием рабочих окон (открытым центром).

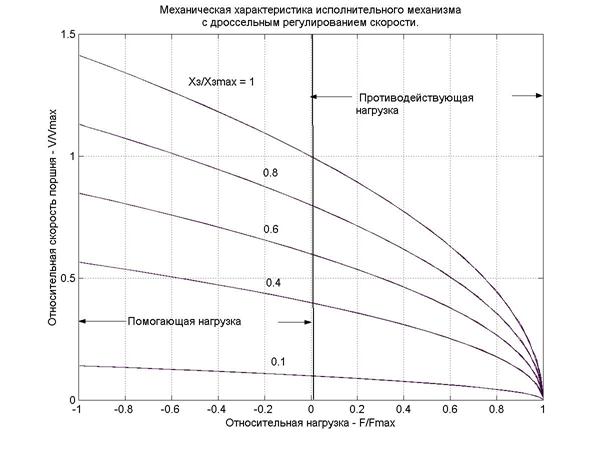
Рис.1.7

Механические характеристики привода с дроссельным регулированием скорости.

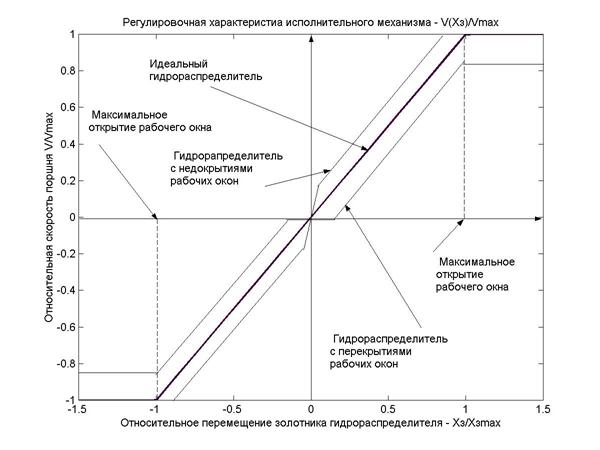
Рис.1.8

Регулировочная характеристика привода с дроссельным регулированием.

В последнем случае в области малых сигналов крутизна скоростной характеристики удваивается, поскольку в формировании потока жидкости в гидроцилиндр участвуют все четыре рабочих окна.

Энергетика привода с дроссельным регулированием скорости.

На рис.1.9 показана упрощенная схема привода с дроссельным регулированием скорости, в который входит нерегулируемый источник гидравлической энергии. Этот источник гидравлической энергии состоит из нерегулируемого насоса и напорного клапана, который поддерживает постоянное давление подачи на входе в гидрораспределитель - Рп. При этом избыток расхода рабочей жидкости перепусается в сливной бак. Ротор насоса приводится во вращение мотором М. Подача насоса выбрана таким образом, что она соответствует максимальной скорости поршня.

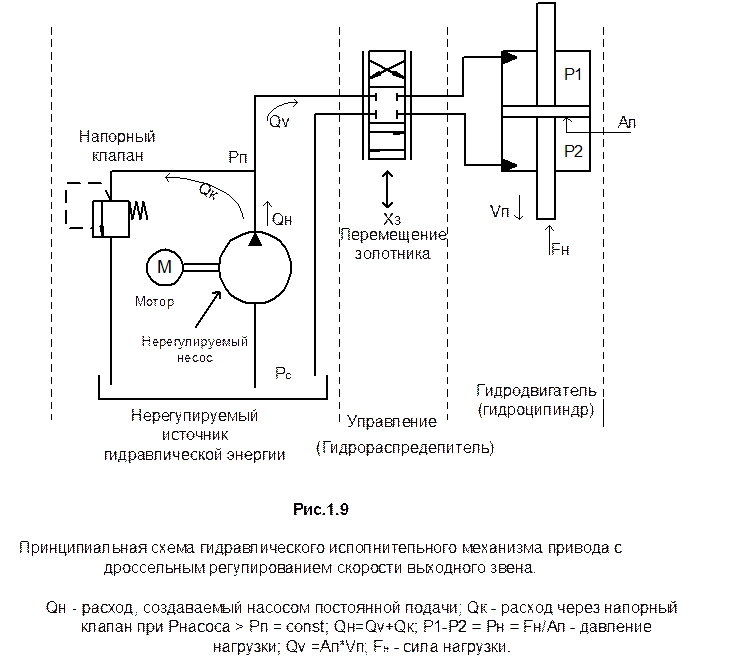
Для такого привода можно записать следующие соотношения:

.

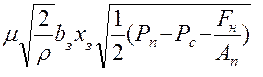При Хз = Хз max и при Fн = 0

Qн =Vп max*Aп, Qк = 0.

При Хз = 0 или при Fн = Ап*(Рп – Рс)

Qv = 0, Qн = Qк.

В безразмерной форме механическую характеристику привода можно представить так, как это показано на рис.1.10 (кривая V(Fн)/Vmax). На этом же рисунке показана зависимость развиваемой приводом мощности – кривая V*Fн/Nmax. Здесь Nmax – максимальная мощность потребляемая приводом, которая определяется одним из следующих выражений:

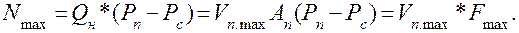
Своего максимума выходная мощность достигает при Fн = (2/3)Fmax.

Геометрическая интерпретацией максимальной выходной мощности исполнительного механизма привода сдроссельным регулированием скорости является площадь области А под кривой механической характеристики.

Точка Fopt – оптимальная нагрузка на привод.

Рис.1.10

Механическая характеристика привода с дроссельным регулированием и распределение энергии в элементах привода:

Величина максимальной выходной мощности привода равна:

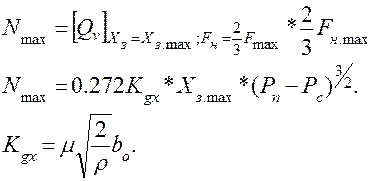
При этом величина оптимальных, но неизбежных потерь мощности, которые образуются на двух гидравлических сопротивлениях (рабочих окнах гидрораспределителя) определяется площадью области В. Эти оптимальные потери мощности равны:

Область С характеризуется расходом жидкости, который направляется в бак через напорный клапан для поддержания постоянным давления подачи. Этот расход равен нулю при Fн = 0, а при Fн = Fmax равен полному расходу насоса – Qн. Указанный расход формируется при перепаде давления на напорном клапане равном Рк = Рп – Рс. Оптимальные потери мощности на этом напорном клапане равны:

.

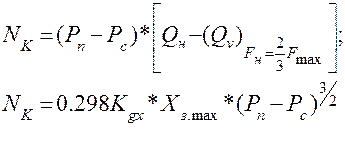Потребляемая приводом мощность определяется следующим выражением:

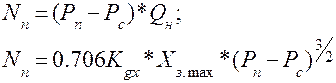
Таким образом, максимальный коэффициент полезного действия (кпд) рассмотренного привода с дроссельным регулированием скорости не превышает оценки 0.385.

Повысить кпд такого привода можно только одним способом – уменьшить или исключить расход через напорный клапан на слив. Это можно сделать путём использования в приводе регулируемого по давлению насоса. На рис.1.11 показана схема привода с дроссельным регулированием скорости выходного звена и с регулированием по давлению насосом.

В таком приводе расход через напорный клапан может появиться только в случае возникновения избыточного давления Рmax, при котором срабатывает клапан. Коэффициент полезного действия такого привода не превышает 0.66. Напорный клапан в таком приводе выполняет функции предохранительного элемента, защищающего привод от перегрузки по давлению (Рmax >Pп).

На практике, на самолетах от одного источника гидравлической энергии с регулируемым по давлению насосом питаются несколько гидравлических приводов, которые работают в различные интервалы времени и с различными нагрузками.

3. Динамические свойства исполнительного механизма привода с дроссельным регулированием скорости.

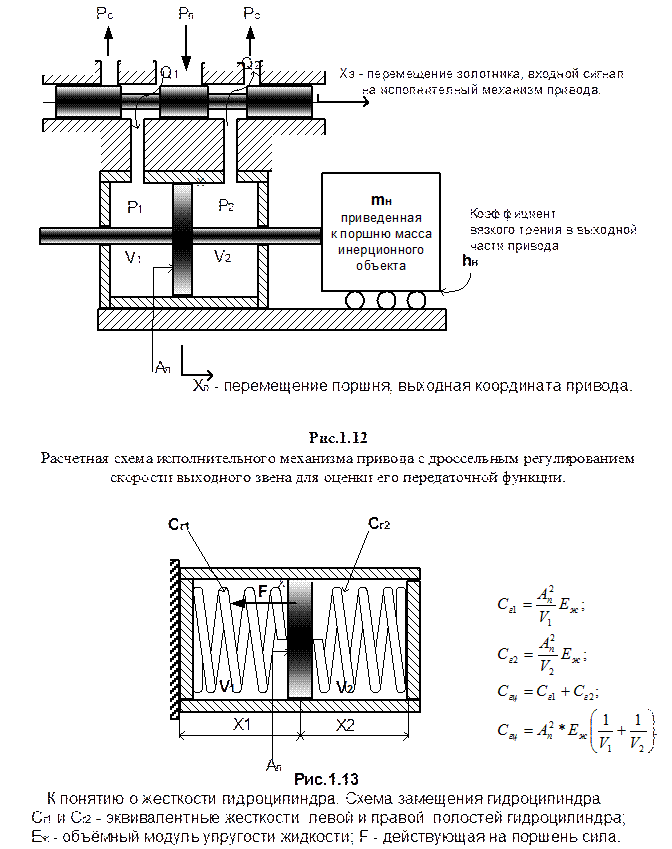
На рис.1.12 показана схема исполнительного механизма привода, управляющего положением инерционного объекта.

На этом рисунке показано, что входным сигналом этого исполнительного механизма является перемещение золотника гидрораспределителя, а выходной координатой - перемещение инерционного объекта, которое совпадает с перемещением поршня.

В основе уравнений, описывающих динамику такого устройства, лежат уравнения баланса потоков рабочей жидкости в магистралях гидрораспределителя и в полостях гидроцилиндра, а также уравнение движения поршня и инерционного объекта под действием силы давления:

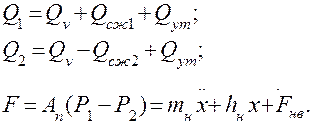
В этих уравнениях составляющие уравнений расхода рабочей жидкости имеют следующий физический смысл:

Q1,2 – расходы жидкости через дросселирующие элементы (рабочие окна) гидрораспределителя;

Qсж.1,2 - расходы рабочей жидкости, которые идут на компенсацию процессов сжатия и расширения рабочей жидкости в полостях гидроцилиндра;

Qут. – расход жидкости из полости в полость гидроцилиндра по зазорам поршня, гидроцилиндра и гидрораспределителя (в определенных случаях – расход через специально введенный канал кольцевания полостей гидроцилиндра);

F – сила на поршне гидроцилиндра, создаваемая перепадом давления на поршне.

Fнв – внешнее силовое воздействие.

Остальные обозначения очевидны из рисунка 1.12.

Выражения для составляющих уравнений баланса потоков жидкости имеют следующий вид:

Здесь Кут – коэффициент утечек жидкости в предположении, что расход утечек определяется линейным законом.

Предположим, что поршень совершает малые перемещения относительно среднего положения (Х1 = Х2), а давление рабочей жидкости в полстях гидроцилиндра Р1 и Р2 изменяются симметрично относительно начального давления в полостях гидроцилиндра, которое для симметричного гидрораспределителя примерно равно Р0=(Рп+Рс)/2. Разложив в ряд Тейлора [2] функции, определяющие расход рабочей жидкости через рабочие окна гидрораспределителя, и оставив первые члены разложения, получим следующие приближенные выражения для расходов Q1 и Q2:

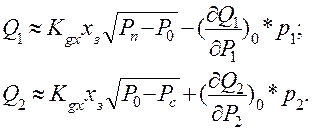
Здесь р1 и р2 малые отклонения давления Р1 и Р2 от Р0. Частные производные составляющих расходов Q1 и Q2 по Р1 и Р2 есть коэффициенты линеаризации параболических зависимостей Q1(P1) и Q2(P2) в точке Р0. Эти частные производные обозначаются, как KQp1 KQp2.

Выражения 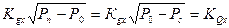есть коэффициенты линеаризации зависимостей Q1(x) и Q2(x) при Р1 = Р2 = Р0.

Два приведенных выше уравнения баланса потоков путем по членного сложения и деления на два объединяются в одно, которое может быть представлено в следующем виде:

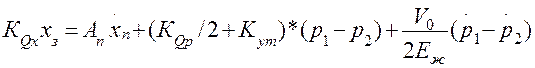
Обозначим:

Рн= р1 –р2 – давление нагрузки.

Кqp.э = (КQp/2+Kут) – эквивалентный наклон механической характеристики гидрораспределителя Q(Pн).

При Fнв = 0, объединяя уравнение движения инерционного объекта с последним уравнением баланса потоков рабочей жидкости в полостях гидроцилиндра и в трактах гидрораспределителя, можно получить передаточную функцию исполнительного механизма привода по отношению к управляющему воздействию (хз) в следующем виде:

.

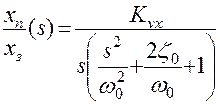Здесь используются следующие обозначения:

Kvx =KQx/Aп – коэффициент усиления исполнительного механизма по скорости (тангенс угла наклона скоростной характеристики исполнительного механизма V (xз);

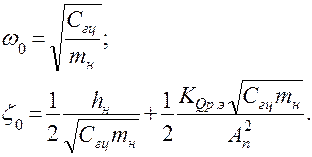
s – оператор преобразования Лапласа [8].
В этих выражениях Сгц – жесткость гидроцилиндра, определяемая, как сумма двух составляющих жесткостей: правой и левой полостей. Выражения, определяющие жесткость гидроцилиндра, и факторы влияющие на неё показаны, на рис.1.14 и рис.1.15.

Поскольку, минимальная жесткость гидроцилиндра имеет место при поршне, который находится в среднем положении, то далее при оценке динамики привода используется это значение жесткости. Геометрическая интерпретация динамических свойств гидроцилиндра, поршень которого соединен с инерционным объектом, показана на рис.1.15. На этом же рисунке приведено уравнение движения инерционного объекта под действием некоторой силы F и передаточная функция одного гидроцилиндра по отношению к внешнему силовому воздействию.

Важно отметить, что демпфирование привода определяется двумя факторами:

§ Суммарными силами трения в гидроцилиндре и в объекте, которые в передаточной функции исполнительного механизма отображаются коэффициентом вязкого трения hн.

§ Утечками рабочей жидкости из полости в полость гидроцилиндра под воздействием перепада давления Рн=Р1-Р2, а также в некоторой степени коэффициентом KQp, который является во многом мало определенным фактором и при оценке динамики приводов его лучше не учитывать.

Оба указанных факторов являются диссипативными факторами и связаны с рассеянием энергии.

4. Основные динамические свойства привода с позиционной обратной связью.

Схема простейшего следящего гидропривода с дроссельным регулированием скорости выходного звена показана на рис.1.16. На этой схеме показан исполнительный механизм привода. Золотник гидрораспределителя перемещается с помощью некоторого электромеханического или электрогидравлического устройства.

Таким устройством может быть:

§ электромеханический преобразователь сигналов (линейный электродвигатель);

§ электрогидравлический усилитель мощности типа «сопло – заслонка» или «струйная трубка»;

§ специальный маломощный сервопривод с электрической обратной связью по положению золотника основного гидрораспределителя.

Последний из указанных вариантов характерен для приводов с большими (свыше 100 л/мин) расходами рабочей жидкости.

Блок-схема следящего привода показана на рис.1.17.

Коэффициент передачи прямой цепи следящего привода определяется выражением:

В этом выражении приняты следующие отношения:

Кiu – коэффициент усиления электрических сигналов;

Кхi – коэффициент передачи устройства управления золотником гидрораспределителя (коэффициент передачи электрогидравлического усилителя мощности - ЭГУ);

Ue – сигнал рассогласования между управляющим сигналом и сигналом позиционной обратной связи.

Структурная схема типового следящего привода с дроссельным регулированием скорости, управляющего положением инерционного объекта, часто представляется в виде, который показан на рис.1.18.

Произведение коэффициента передачи прямой цепи по скорости на коэффициент позиционной обратной связи представляет собой добротность следящего привода – KD.

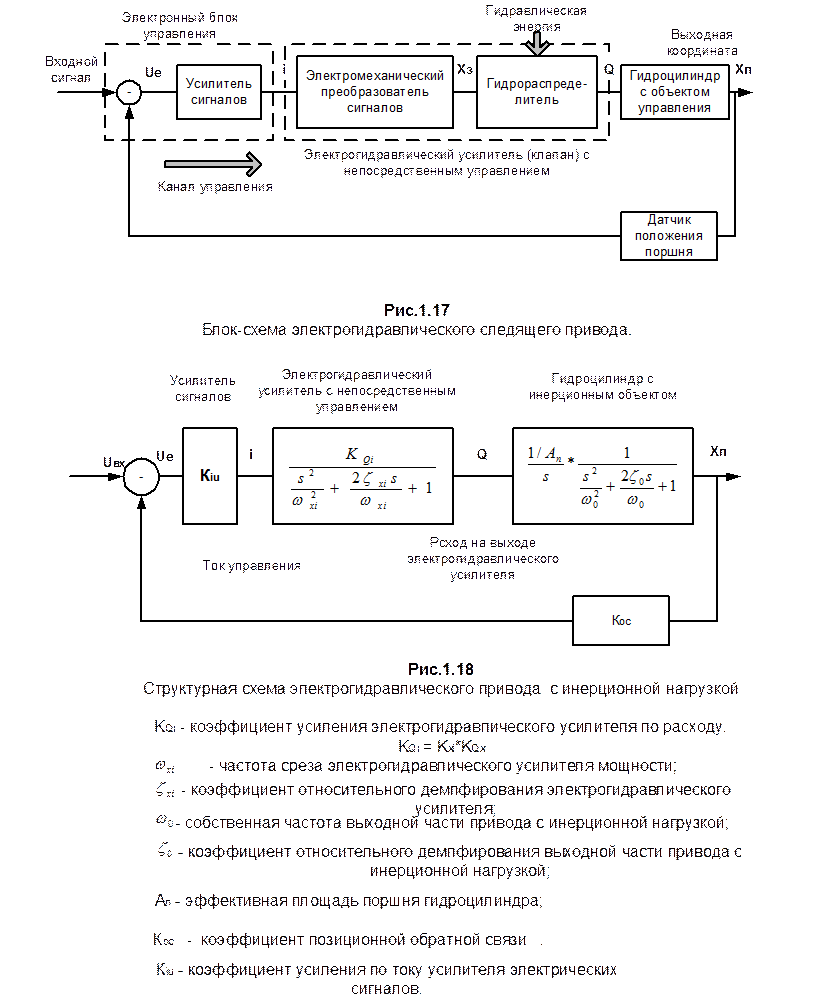
С учетом приведенных обозначений передаточная функция разомкнутого привода имеет следующий вид:

.

Из этого выражения можно выделить функционал, который является передаточной функцией электрогидравлического усилителя мощности (или мощного электромеханического преобразователя сигналов, или сервопривода) по перемещению золотника основного гидрораспределителя:

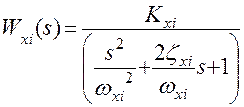
Такая передаточная функция приближенно описывает наиболее существенные динамические свойства большинства устройств, преобразующих электрический сигнал в виде тока управления iу или входного напряжения сервопривода золотника основного гидрораспределителя привода в перемещение его золотника (Хз) в диапазоне частот управления авиационными приводами.

wxi - частота среза указанного устройства (электрогидравлического усилителя, преобразователя сигналов или сервопривода), т.е. частота, на которой фазочастотная характеристика достигает уровень -90°.

xxi - коэффициент относительного демпфирования преобразователя сигналов.

Во многих проектных случаях электрогидравлические усилители мощности обладают высоким быстродействием, которое характеризуется параметром wxi. Если выполняется условие

,

то передаточная функция разомкнутого контура привода может быть представлена без существенной погрешности в следующем виде:

.

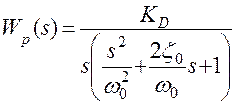Фазочастотная характеристика разомкнутого контура такого привода пересекает линию - 180° всегда на частоте . Это обстоятельство позволяет производить оценку устойчивости следящего привода [9] путем проверки следующего простого условия:

.

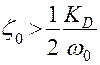Если условие не выполняется, то оценку устойчивости привода следует осуществлять с учетом динамики устройства, преобразующего сигнал управления в перемещение золотника гидрораспрелителя (электрогидравлического усилителя мощности, электромеханического преобразователя сигналов или сервопривода).

Передаточная функция замкнутого привода при выполнении условия представляется в виде:

.

Эта передаточная функция приближенно характеризует динамические свойства следящего привода, управляющего положением инерционного объекта.

Если привод установлен на упругом основании с жесткостью Со и соединен с инерционным объектом упругой механической системой (проводкой) с жесткостью Сп, так как это показано на рис.1.19, то передаточная функция замкнутого по положению поршня привода определяется выражением:

,

В этой передаточной функции приняты следующие обозначения:

wос – собственная частота системы привода установленного на упругом основании с жесткостью Со, и жесткостью силовой проводки от поршня к инерционному объекту Сп;

xос – коэффициент относительного демпфирования системы привода.

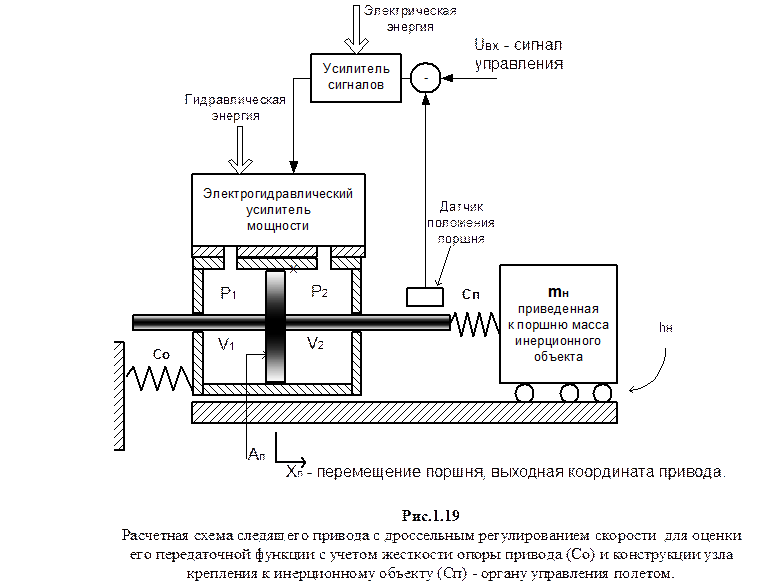
Указанные параметры определяются следующими выражениями:

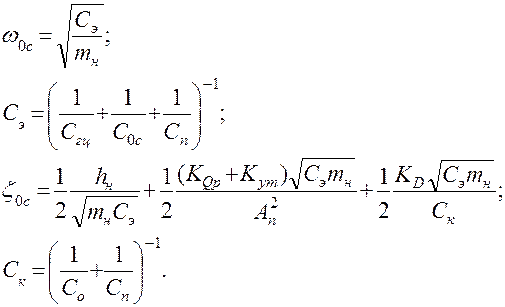
На первый взгляд приведенное выражение показывает, что снижением жесткости конструкции (Ск) можно увеличить устойчивость привода, поскольку с уменьшением этого параметра увеличивается третья из составляющих демпфирования. Однако можно показать, что снижением Ск нельзя увеличить запас устойчивости привода по амплитуде. В соответствии с условием устойчивости привода

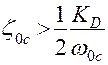
снижением жесткости конструкции установочных узлов привода Ск нельзя увеличить приведенное выше неравенство в сторону увеличения запасов устойчивости, т.к. при уменьшении жесткости конструкции одновременно с увеличением демпфирования снижается и собственная частота привода. На рисунках 1.20, 1.21, 1.22 показаны динамические характеристики типового следящего привода, частота среза электрогидравлического усилителя мощности (ЭГУ) которого примерно в три раза превышает собственную частоту исполнительного механизма с инерционной нагрузкой.

Расчет этих характеристик производился с учетом и без учета динамики ЭГУ. На рис.1.20 представлены логарифмические частотные разомкнутого контура привода с учетом динамики ЭГУ.

Рис.1.20

На рис.1.21 показаны те же характеристики, но без учета динамики ЭГУ. На этих характеристиках показаны запасы устойчивости привода по амплитуде Gm и по фазе – Pm. На рис.1.22 показаны переходные процессы следящего привода на ступенчатый сигнал с учетом динамики ЭГУ – G2 и без учета динамики ЭГУ – G1. Сравнивая приведенные характеристики можно предположить, что для предварительной оценки динамики следящего привода при выполнении неравенства можно динамику ЭГУ или другого устройства, выполняющего его функции, не учитывать.

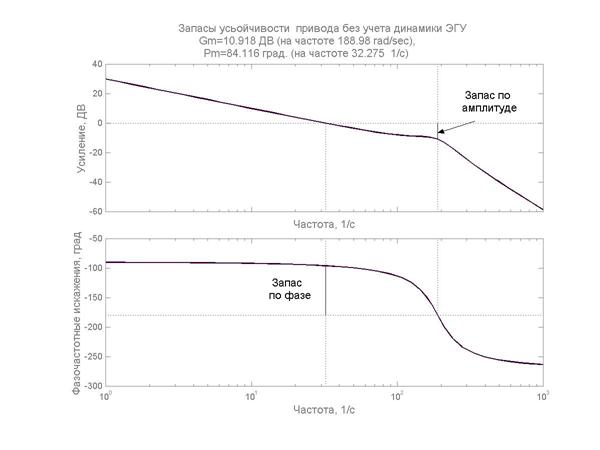
Рис.1.21

Рис.1.22

5. Динамическая жесткость привода.

Если полученная выше передаточная функция привода характеризует динамические свойства привода, как элемента системы управления полетом самолета, то динамическая жесткость характеризует жесткость привода, как элемента планера самолета. Указанная жесткость зависит от частоты изменения внешней силы и во многом определяет безопасность от флаттера. Дело в том, если в рулевой поверхности одновременно существуют изгибные и крутильные колебания, то при определенной скорости полета самолета подводимая из воздушного потока энергия, определяемая скоростью полета, может вызвать изгибные колебания с нарастающей амплитудой, которые приводят к разрушению конструкции. Энергия, определяемая скоростью полета самолета и подводимая из вне, пропорциональна квадрату скорости полета самолета, а рассеяние энергии в системе «рулевая поверхность – рулевой привод» пропорционально частоте колебаний рулевой поверхности. Указанные колебания происходят с собственной частотой упругой системы «рулевая поверхность – рулевой привод». Собственная частота этой системы определяется следующим общим соотношением:

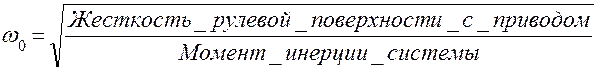
Поэтому увеличение жесткости системы рулевого привода способствует увеличению рассеяния энергии, т.е. увеличению безопасности от флаттера.

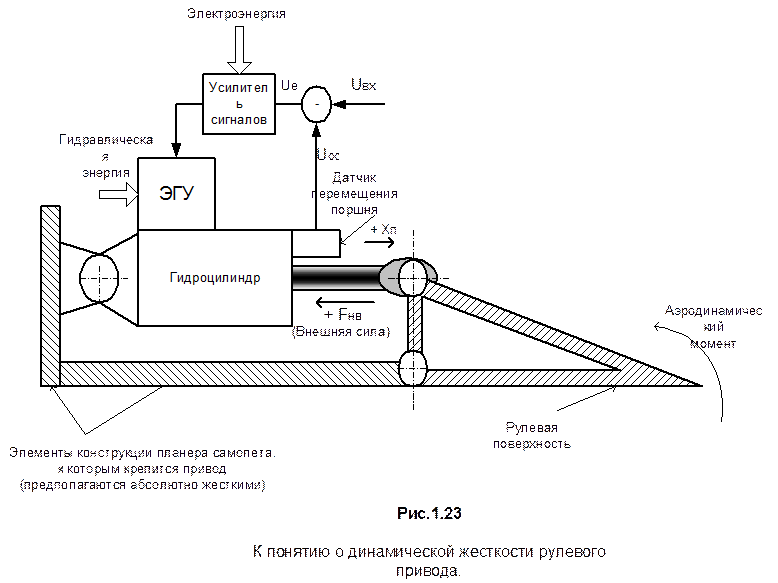
Схема рулевого привода, подключенного к рулевой поверхности самолета показана на рис.1.23.

Под динамической жесткостью привода понимается передаточная функция привод, определяющая отношение внешней силы Fнв(s) к перемещению штока гидроцилиндра, вызванного этой силой Хп (s). Указанная передаточная функция может быть получена из приведенных выше линеаризованных уравнений динамики привода при mн=0, hн=0, Uвх=0, Fнв=Fo*sinwt. В предположении, что ЭГУ является безинерционным элементом, передаточная функция динамической жесткости имеет следующий вид:

.

Здесь – статическая жесткость следящего привода.

Статическая жесткость привода и постоянная времени гидроцилиндра (Тгц) через его параметры определяется следующим образом:

Крu – коэффициент усиления прямой цепи привода по перепаду давления в гидроцилиндре: Kpu@ (Р1-Р2)max/Ue.max. Можно показать, что с увеличением частоты изменения внешней силы динамическая жесткость привода стремится к жесткости гидроцилиндра:

На рис.1.24 представлены частотные характеристики динамической жесткости рулевого привода, полученные по приведенному выше выражению. Эти характеристики получены при двух наборах параметров привода. Следует отметить, что при сравнительно низкой добротности привода (KD<1/Тгц) фазочастотная характеристика привода положительна, т.е. привод обладает демпфирующими свойствами. При относительно высокой добротности привода (KD > 1/Тгц) фазочастотная характеристика привода - отрицательна и, следовательно, привод не обладает демпфирующими свойствами.

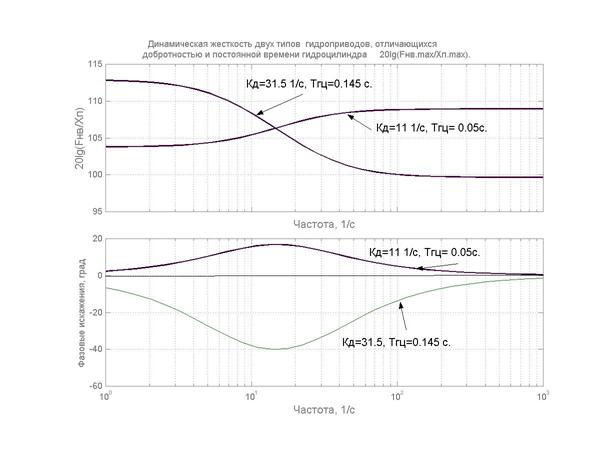
Рис.1.24

Представляет практический интерес оценка динамической жесткости привода, находящегося в отключенном состоянии. При отключении давления подачи привода и включении канала межполостных перетечек в гидроцилиндре с линеаризованной проводимостью Gл. Расчетная схема привода для оценки динамической жесткости привода, который находится в отключенном состоянии показана на рис.1.25.

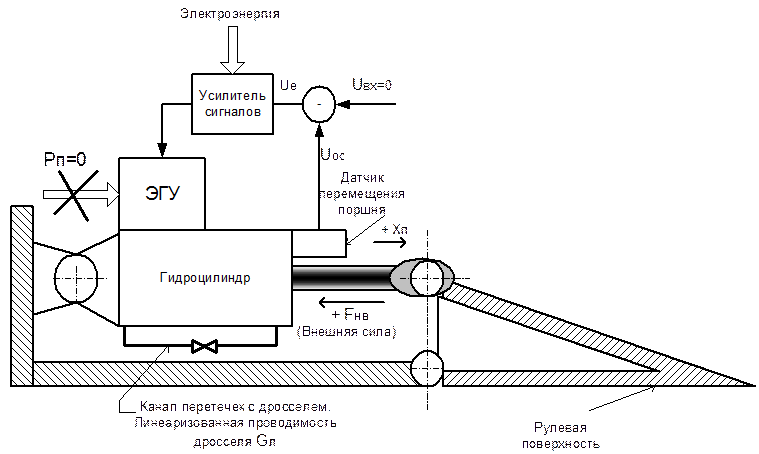
Рис.1.25

Схема привода рулевой поверхности самолета при отказе гидравлического питания

Передаточная функция динамичесой жесткости привода в отключенном состоянии имеет следующий вид:

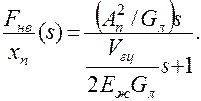
Очевидно, что в этом случае привод в области низких частот динамическая жесткость описывается дифференцирующим звеном с коэффициентом (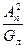), т.е. представляет собой идеальный демпфер. Начиная с частоты 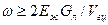, динамическая жесткость привода стремится к жесткости гидроцилиндра Сгц.

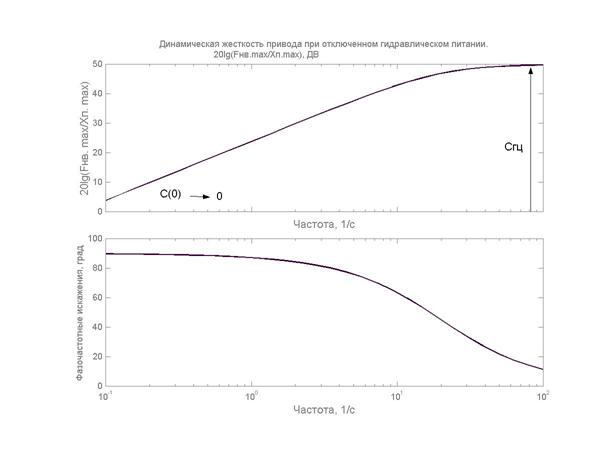
Рис.1.26.

Динамическая жесткость рулевого привода при отказе гидравлического питания и включённом канале кольцевания полостей гидроцилиндра.

Дата добавления: 2014-01-07