Основные свойства линейных, параметрических и нелинейных цепей

Классификация цепей и этапы их анализа

Общая классификация сигналов

РАЗНОВИДНОСТИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ И ЦЕПЕЙ

ВВЕДЕНИЕ

Курс «Теория электрических цепей» является одной из базовых дисциплин, необходимых для теоретической и профессиональной подготовки инженеров в промышленной электронике, и служит основой для последующего изучения многих специальных курсов. Целью курса является изучение фундаментальных методов анализа и синтеза линейных систем, а также процессов обработки и преобразования сигналов в таких системах.

Курс «Теория электрических цепей» является обязательной дисциплиной для студентов всех форм обучения специальности «Промышленная электроника» физико-технического факультета УО «Гродненский государственный университет им. Янки Купалы». Данное пособие в первую очередь предназначено студентам заочного отделения, изучающим этот курс в течение двух семестров, поскольку в нем в доступной форме изложены основные разделы теоретического материала, необходимые им для самостоятельной подготовки контрольных работ и курсовых проектов.

Настоящее пособие позволит студентам изучить и освоить вопросы классификации сигналов и цепей; принципы математического описания физических процессов в линейных системах; временной, спектральный и операторный методы анализа этих систем; основные положения теории синтеза электронных схем, в том числе и активных фильтров; и, наконец, основы теории согласованной фильтрации.

Глубокое понимание и овладение вопросами данного курса необходимо для теоретической и практической подготовки инженеров во всех отраслях промышленности, поскольку они служат логическим фундаментом для изучения последующих дисциплин и дальнейшей профессиональной деятельности.

Несмотря на то, что промышленная электроника является быстро развивающейся отраслью знаний как в научном, так и в техническом плане, традиционные идеи и методы, принципиальные вопросы анализа и синтеза электронных схем остаются необходимыми для инженеров, и их изучению, безусловно, с учетом современных требований и тенденций развития данной сферы, посвящен курс «Теория электрических цепей» и данное учебно-методическое пособие.

1.1. Общая классификация сигналов.

1.2. Общая классификация электрических цепей и этапы их анализа.

1.3. Основные свойства линейных, параметрических и нелинейных цепей.

Изучение каких-либо новых объектов или явлений, как правило, предполагает проведение их предварительной классификации. Для этого, в первую очередь, необходимо выработать критерии классификации и установить соответствующую терминологию. Можно сказать, что электрический сигнал представляет собой физический (электрический) процесс, несущий в себе информацию. Количество информации, которое можно передать с помощью некоторого сигнала, зависит от основных его параметров: длительности, полосы частот, мощности и т.д.

Для того, чтобы сигналы как физические процессы можно было бы сделать объектами теоретического изучения и расчетов, необходимо создать математическую модель исследуемого сигнала, т.е. функциональную зависимость, аргументом которой, как правило, является время (s(t), u(t), f(t)). Математическая модель позволяет абстрагироваться от конкретной природы носителя сигнала. Функции, описывающие сигналы, могут принимать как вещественные, так и комплексные значения, поэтому можно говорить о вещественных и комплексных моделях сигналов. Знание математических моделей сигналов дает возможность их сравнения, установления тождества и различий и проведения классификации.

Итак, первым критерием классификации сигналов является их размерность. Различают одномерные и многомерные сигналы. Сигнал, описываемый одной функцией времени, называется одномерным (напряжение на зажимах какой-либо цепи или ток, протекающий в ветви). Многомерные сигналы образуются некоторым упорядоченным множеством одномерных сигналов (система напряжений на зажимах многополюсника):

V (t) = {v₁(t), v₂(t),..., v_N(t)},

где N называется размерностью сигнала.

Другой принцип классификации сигналов основан на возможности или невозможности точного предсказания их мгновенных значений в любые моменты времени (критерий определенности или детерминированности). Если математическая модель позволяет сделать такое предсказание с вероятностью единица, т.е. априори известно поведение сигнала в любой момент времени, то сигнал называется детерминированным. Способы задания такого сигнала могут быть различными - математическая формула, вычислительный алгоритм и т.д. Примерами детерминированных сигналов могут служить импульсы или пачки импульсов, форма, величина и положение во времени которых известны, а также непрерывный сигнал с заданными амплитудными и фазовыми соотношениями внутри его спектра. Детерминированные сигналы можно подразделить на периодические и непериодические. Периодическим называется любой сигнал, для которого выполняется условие s(t) = s(t + nT), где период Т является конечным отрезком, а n – любое целое число.

Простейшим периодическим детерминированным сигналом является гармоническое колебание (ток, напряжение, заряд, напряженность поля), определяемое законом

s(t) = A cos (2pt/T + j) = A cos (wt + j), -¥ < t < ¥,

где А, Т, w и j - постоянные амплитуда, период, угловая частота и начальная фаза колебания. Строго гармоническое колебание называют монохроматическим. Любой сложный периодический сигнал, как известно, можно представить в виде суммы гармонических колебаний с частотами, кратными основной частоте w = 2p/T. Основной характеристикой сложного периодического сигнала является его спектральная функция, содержащая информацию об амплитудах и фазах отдельных гармоник. Непериодическим детерминированным сигналом называется любой детерминированный сигнал, для которого не выполняется условие s(t) = s(t + nT).

Строго говоря, детерминированных сигналов в природе не существует. Неизбежное взаимодействие источника сообщений с окружающими физическими объектами, наличие хаотических влияний заставляет рассматривать реальные сигналы как случайные функции времени, т.е. как случайные сигналы - сигналы, значения которых заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью, меньшей единицы. Для характеристики и анализа случайных сигналов применяется статистический подход. В качестве основных характеристик случайных сигналов принимают закон распределения вероятностей и спектральное распределение мощности сигнала. Между детерминированными и случайными сигналами нет четкой границы, однако в условиях, когда уровень помех значительно меньше уровня полезного сигнала с известной формой, более простая детерминированная модель оказывается вполне адекватной поставленной задаче. Изучению и анализу свойств случайных сигналов посвящен большой раздел радиофизики - статистическая радиотехника, основанная на математическом аппарате теории вероятностей и теории случайных процессов.

Очень важный для радиотехники класс сигналов представляют собой импульсные сигналы, т.е. колебания, существующие лишь в пределах конечного отрезка времени. При этом различают видеоимпульсы (рис.1.1, а) и радиоимпульсы (рис.1.1, б).

а) б) в)

Рис. 1.1 – Импульсные сигналы и их характеристики:

а) видеоимпульс; б) радиоимпульс; в) определение числовых параметров импульса

Различие между этими двумя основными видами импульсов состоит в следующем. Если и_в(t) – функция видеоимпульса, то соответствующий ему радиоимпульс опишется выражением:

u_p(t) = u_в(t) cos(w₀ t + j₀),

где частота w₀ и начальная фаза j₀ произвольны. При этом и_в(t) называется огибающей радиоимпульса, а функция cos(w₀ t + j₀) - его заполнением. В технических расчетах, как правило, используют следующие основные параметры импульсных сигналов: А - амплитуду - максимальную высоту (для трапециевидных импульсов) и временные параметры: t_u - длительность импульса, активная длительность (измеряется на уровне 0,5А), t_ф - длительность фронта (время нарастания импульса от 0,1А до 0,9А), t_c - длительность среза (время спада импульса от 0,9А до 0,1А).

И, наконец, последний и основной критерий классификации сигналов - по их виду (или структуре). Применяемые в современной электронике сигналы можно разделить на следующие классы:

n сигналы, произвольные по величине и непрерывные по времени (рис.1.2, а);

n сигналы, произвольные по величине и дискретные по времени (рис.1.2, б);

n сигналы, квантованные по величине и непрерывные по времени (рис.1.2, в);

n сигналы, квантованные по величине и дискретные по времени (рис.1.2, г).

Сигналы первого класса иногда называют аналоговыми (так как их можно трактовать как электрические модели физических величин) или непрерывными - континуальными (так как они задаются по оси времени на несчетном множестве точек). При этом по оси ординат они могут принимать любое значение в определенном интервале.

Второй класс сигналов - дискретные. Они задаются при дискретных значениях времени (на счетном множестве точек) (отсюда и название); величина же сигнала в этих точках может принимать любое значение в определенном интервале по оси ординат. Простейшая математическая модель дискретного сигнала s_д(t) - это счетное множество точек {t_i}, i = 1, 2, 3,..., на оси времени, в каждой из которых определено отсчетное значение сигнала s_i. Как правило, шаг дискретизации D = t_i+1 - t_i для каждого сигнала постоянен, и для быстро изменяющихся во времени сигналов мал.

В принципе, любому медленно изменяющемуся во времени аналоговому сигналу можно поставить в соответствие его дискретный образ, имеющий вид последовательности прямоугольных видеоимпульсов одинаковой длительности и высоты, соответствующей значению импульса в отсчетных точках; либо одинаковой высоты и различной длительности в соответствии с текущими отсчетными значениями.

а) б) в) г)

Рис. 1.2 – Разновидности сигналов:

а) - аналоговые; б) - дискретные; в) - квантованные; г) цифровые

Третий класс - сигналы, квантованные по уровню. Они задаются на всей временной оси, однако величина сигнала может принимать лишь дискретные значения.

Таким образом, термин дискретный будет применяться только по отношению к дискретизации по времени; дискретизация по уровню будет обозначаться термином квантование.

Четвертый класс сигналов - цифровые, т.е. дискретные по времени и квантованные по уровню, при этом уровни можно пронумеровать числами с конечными числом разрядов, что используется при представлении сигналов в цифровой форме с помощью цифрового кодирования (как правило, в двоичной системе счисления).

Каждому из этих классов сигналов можно поставить в соответствие аналоговую, дискретную или цифровую цепи. Связь между видом сигнала и видом цепи показана на рис. 1.3.

При обработке аналогового сигнала с помощью аналоговой цепи не требуется дополнительных преобразований сигнала. При обработке аналогового сигнала с помощью дискретной цепи необходимы два преобразования: дискретизация сигнала на входе дискретной цепи (из 1 во 2) и обратное преобразование на выходе (из 2 в 1). При цифровой обработке аналогового сигнала требуется еще два дополнительных преобразования: аналог-цифра, т.е. квантование и цифровое кодирование на входе цифровой цепи (из 2 в 4), и обратное преобразование – цифра-аналог (ЦАП), т.е. декодирование на выходе цифровой цепи (из 4 во 2).

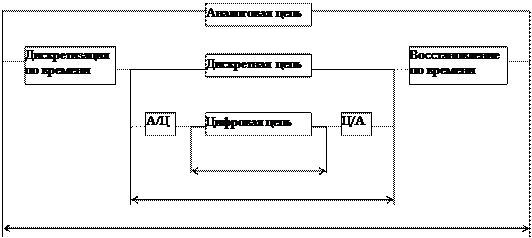Цифровой сигнал

Дискретный сигнал

Аналоговый сигнал

Рис. 1.3 – Виды сигнала и соответствующие им цепи

Основные электротехнические преобразования осуществляются с помощью большого числа линейных и нелинейных элементов и цепей. Линейные цепи, в свою очередь, подразделяются на цепи с постоянными и цепи с переменными параметрами. Последние часто называют параметрическими цепями.

Каждый из перечисленных классов цепей подразделяется, кроме того, на цепи с сосредоточенными и с распределенными параметрами. К первым относятся цепи, составленные из катушек индуктивности, конденсаторов и резисторов, а ко вторым - цепи, содержащие линии, волноводы, излучающие системы.

Этот критерий классификации электротехнических систем основан на сопоставлении физических размеров системы и длины волны колебаний, подаваемых на ее вход. Если характерный размер системы (например, наибольшая длина соединительных проводников электрической цепи) оказывается гораздо меньше длины волны, то это будет система сосредоточенного типа. В сосредоточенной цепи всегда можно выделить физические области с преимущественной локализацией энергии электрического поля (конденсаторы) и магнитного поля (катушки индуктивности). Свойства сосредоточенных цепей не зависят от конфигурации проводников, поэтому их принято описывать абстрактными моделями – принципиальными схемами. Анализ и расчет таких систем проводится на основании законов Кирхгофа и Ома.

На частотах от нескольких тысяч МГц (больше 10⁹ Гц), в СВЧ диапазоне, физические размеры большинства устройств становятся сравнимыми с длиной волны передаваемых колебаний. При этом становится необходимым учет времени распространения сигнала вдоль системы. Обычные электрические цепи в столь высокочастотном диапазоне использоваться уже не могут, и такие системы называются системами с распределенными параметрами (распределенные или волновые системы). Так, вместо проводов применяются объемные металлические трубы – волноводы, вместо колебательных контуров – их распределенные аналоги, называемые резонаторами. Теория, методы анализа и проектирования распределенных систем достаточно сложны и служат содержанием отдельных курсов.

В любом случае исследование любой реальной цепи разбивается на четыре этапа:

1. Составление математической модели исследуемой цепи. Реальная цепь содержит бесконечное число степеней свободы, которые определяются различными связями между элементами цепи. Схема, в которой учтены только основные параметры реальной цепи, называется идеализированной схемой или математической моделью. Выбор основных параметров для модели зависит от их влияния на процессы, протекающие в цепи, и от поставленных задач. Чем больше учтено параметров, тем точнее модель, но тем сложнее ее анализ.

2. Составление дифференциальных уравнений математической модели и их решение.

3. Исследование полученных решений и определение характеристик исследуемой цепи.

4. Проведение эксперимента и сравнение экспериментальных результатов с теоретическими – позволяет определить правильность выбранной модели и точность приближенных методов решения полученных дифференциальных уравнений. В результате иногда возможен переход к новой более совершенной модели.

В данном курсе изучаются цепи с сосредоточенными параметрами. Для выявления основных свойств указанных цепей необходимо напомнить свойства описывающих эти цепи дифференциальных уравнений. Линейная цепь с постоянными параметрами состоит из линейных элементов, параметры которых не зависят от времени и протекающего через них тока или приложенного напряжения, и характеризуется линейным дифференциальным уравнением с постоянными коэффициентами. Линейная цепь с переменными параметрами характеризуется линейным дифференциальным уравнением, в котором по крайней мере один из коэффициентов является функцией времени. И, наконец, нелинейная цепь будет характеризоваться нелинейным дифференциальным уравнением, в котором хотя бы один из коэффициентов является функцией не только времени, но и самого сигнала.

Для определения свойств линейной цепи с постоянными параметрами запишем уравнение для тока i(t) в последовательном колебательном контуре, содержащем L, C, r и э.д.с. e(t):

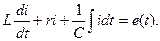(1.1)

Уравнение (1.1) является линейным, если коэффициенты L, r и 1/C не зависят от величины тока i, или, что то же самое, от величины внешней силы e(t). При выполнении этого условия напряжения на каждом из элементов контура линейно связаны с током:

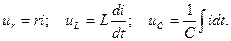(1.2)

Т.к. дифференцирование и интегрирование являются операциями линейными, можно утверждать, что u_L и u_C линейно связаны с током i при любом законе изменения последнего во времени. Для u_r это утверждение еще более очевидно.

Одним из проявлений линейности цепи является независимость соотношения между входными и выходными напряжениями (токами) от уровня входного напряжения (тока). В частности, при изменении тока по закону i = I sin wt получим:

(1.3)

Изменение амплитуды тока I в n раз дает такое же изменение амплитуды напряжения на элементах r, L, C. Это свойство линейных элементов можно толковать как результат линейности их вольт-амперных характеристик (зависимость амплитуды тока от амплитуды напряжения).

Другим важным свойством линейных цепей, также вытекающим из линейности соответствующего дифференциального уравнения, является выполнение принципа независимости (суперпозиции = наложения): при действии на линейную цепь нескольких внешних сил поведение цепи (ток, напряжение) можно определять путем наложения (суперпозиции) решений, найденных для каждой из сил в отдельности. ИЛИ: В линейной цепи сумма эффектов от различных воздействий совпадает с эффектом от суммы воздействий. При этом предполагается, что цепь свободна от начальных запасов энергии.

Еще одно важное свойство линейных цепей с постоянными параметрами вытекает из теории интегрирования линейных дифференциальных уравнений с постоянными коэффициентами. Разложив e(t) в правой части уравнения (1.1) с помощью ряда или интеграла Фурье на простейшие гармонические составляющие, можно получить для каждой составляющей с частотой w_n решение уравнения (1.1) в виде гармонического колебания той же частоты:

i_n(t) = I_n cos (w_nt + j_n),

где I_n и j_n – постоянные амплитуда и фаза.

Отсюда следует, что при любом сколь угодно сложном воздействии в линейной цепи с постоянными параметрами не возникает новых частот, т.е. ни одно из преобразований сигналов, сопровождающихся появлением новых частот (частот, отсутствующих в спектре входного сигнала), не может в принципе быть осуществлено с помощью линейной цепи с постоянными параметрами.

Далее кратко рассмотрим свойства линейных цепей с переменными параметрами. Для них также выполняется принцип суперпозиции (наложения). Однако даже простейшее гармоническое воздействие создает в линейной цепи с переменными параметрами сложное колебание, имеющее спектр частот. Это можно пояснить следующим примером. Пусть к резистору, сопротивление которого изменяется во времени по закону R(t) = R₀ / (1 + M cos Wt), приложена гармоническая э.д.с. e(t) = E₀ cos wt.

Ток через сопротивление определится как:

i(t) = e(t)/R(t) = (E₀ /R₀) (1 + M cosWt) cos wt =

= (E₀/R₀) [cos wt + (M/2) cos (w + W)t +(M/2) cos (w - W)t].

Отсюда видно, в составе тока имеются компоненты с частотами (w ± W), которых нет в e(t), т.е. изменяя во времени сопротивление, можно осуществить преобразование спектра входного сигнала.

Рассмотрим, наконец, общие свойства нелинейных цепей. Из теории нелинейных дифференциальных уравнений известно, что при решении этих уравнений принцип наложения неприменим. Это свойство нелинейных цепей тесно связано с кривизной вольт-амперных характеристик нелинейных элементов (например, диода, рис.1.4, б). В отличие от вольт-амперной характеристики линейного резистора (рис.1.4, а) в данном случае между током и напряжением нет прямой пропорциональности.

а) б)

Рис. 1.4 - Вольт-амперные характеристики: а) - линейного резистора; б) - диода.

Неприменимость для нелинейных цепей принципа наложения делает непригодными спектральный и иные методы анализа, основанные на разложении сложного сигнала на составляющие.

Другим важным свойством нелинейной цепи является преобразование спектра сигнала. При воздействии на нелинейную цепь простейшего гармонического сигнала в цепи, помимо основной частоты, возникают гармоники с частотами, кратными основной частоте. С точки зрения преобразования спектра сигнала следует подчеркнуть принципиальное различие между линейными параметрическими и нелинейными цепями. В линейной параметрической цепи структура спектра зависит только от формы входного сигнала, а в нелинейной – и от формы, и от амплитуды.

Основные радиотехнические процессы: генерация, модуляция, детектирование и преобразование частоты – сопровождаются трансформацией частотного спектра. Поэтому эти процессы можно осуществить с помощью либо нелинейных цепей, либо линейных, но с изменяющимися параметрами. В некоторых случаях используются одновременно как нелинейные, так и линейные параметрические цепи. Вообще, применение тех или иных цепей определяется рабочим диапазоном частот. Поэтому полная классификация радиотехнических цепей не может быть проведена в отрыве от используемых диапазонов частот.

Дата добавления: 2014-01-07