Элементы теории ортогональных сигналов

ОСНОВЫ ТЕОРИИ АНАЛИЗА СИГНАЛОВ

2.1. Элементы теории ортогональных сигналов.

2.2. Спектральный анализ периодических сигналов.

2.3. Спектральный анализ непериодических сигналов. Преобразование Фурье.

2.4. Основные свойства преобразования Фурье.

2.5. Распределение энергии в спектрах периодических и непериодических сигналов.

Теория и техника формирования и обработки сигналов предполагает разложение заданной функции по различным ортогональным системам функций. Напомним основные определения, относящиеся к свойствам ортогональных систем.

Бесконечная система действительных функций

v₀(x), v₁(x), v₂(x),..., v_n(x) (2.1)

называется ортогональной на отрезке [a, b], если

при n¹m. (2.2)

При этом предполагается, что

(2.3)

т.е. что никакая из функций рассматриваемой системы (2.1) не равна тождественно нулю. Условие (2.2) выражает попарную ортогональность функций системы (2.1). Величина 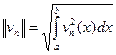называется нормой функции v_n(x). (Это понятие аналогично понятию длины вектора в математике).

Функция v_n(x), для которой выполняется условие

, (2.4)

называется нормированной функцией, а система нормированных функций v₁(x), v₂(x),..., в которой каждые две различные функции взаимно ортогональны, называется ортонормированной системой. Говорят, что при этом в пространстве сигналов задан ортонормированный базис.

Произвольный сигнал s(t) можно разложить в ряд в выбранном ортонормированном базисе:

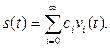(2.5)

Представление (2.5) называется обобщенным рядом Фурье сигнала s(t) в выбранном базисе. Коэффициенты этого ряда находят следующим образом. Возьмем базисную функцию v_k с произвольным номером k, умножим на нее обе части равенства (2.5) и затем проинтегрируем результаты по интервалу времени, в котором заданы сигналы:

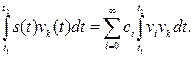(2.6)

Ввиду ортонормированности базиса в правой части (2.6) остается только член суммы с номером i = k, поэтому

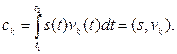(2.7)

т.е. коэффициенты обобщенного ряда Фурье определяются как скалярные произведения разлагаемого сигнала и соответствующих базисных векторов.

Возможность представления сигналов посредством обобщенных рядов Фурье имеет принципиальное значение. Вместо изучения функциональной зависимости на несчетном множестве точек, мы получаем возможность характеризовать эти сигналы счетной (но, вообще говоря, бесконечной) системой коэффициентов обобщенного ряда Фурье, которые представляют собой проекции вектора s(t) в ортонормированном пространстве на базисные направления. Кроме этого, обобщенный ряд Фурье обладает следующим важным свойством: при заданной системе функций v_n(x) и при фиксированном числе слагаемых ряда (2.5) он обеспечивает наилучшую аппроксимацию (в смысле минимума среднеквадратической ошибки) данной функции сигнала s(t).

Ортогональная система называется полной, если увеличением числа членов в ряде среднеквадратическую ошибку можно сделать сколь угодно малой. Условие полноты можно записать в виде соотношения:

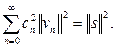(2.8)

Применительно к сигналам s(t) выражение (2.8) принимает энергетический смысл:

(2.9)

Здесь s²(t₀) – мгновенная мощность сигнала в данный момент времени (P=I²R=U²/R). При этом, если под s(t) подразумевается электрическое колебание (ток, напряжение), то Е есть не что иное, как энергия сигнала в промежутке (t₂ - t₁) (при условии, что сопротивление, в котором выделяется энергия, равно 1 Ом).

Таким образом, в соответствии с (2.8) энергия сигнала при использовании ортонормированной системы функций v_n(t) определится как:

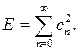(2.10)

Смысл полученного выражения: энергия сигнала равна сумме энергий всех компонент, из которых складывается обобщенный ряд Фурье. При этом имеется в виду, что промежуток времени (t₂ - t₁), в котором определяется энергия Е, является интервалом ортогональности для системы функций v_n(t).

Очевидно, что средняя за время (t₂ - t₁) мощность сигнала:

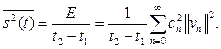(2.11)

Выбор наиболее рациональной ортогональной системы функций определяется видом исследуемых сигналов, поставленными задачами и выбранными методами анализа (синтеза). Так, при дискретизации непрерывных сигналов используют функции вида sinc x; при цифровой обработке сигналов - кусочно-непрерывные функции Уолша. Наибольшее распространение получили тригонометрическая {cos nx, sin nx} и экспоненциальная {exp (inx)} полные ортогональные системы базисных функций. Это объясняется следующими причинами. Во-первых, гармоническое колебание является единственной функцией времени, сохраняющей свою форму при прохождении колебания через любую линейную цепь с постоянными параметрами, при этом изменяется лишь амплитуда и фаза колебания. Во-вторых, разложение сложного сигнала по синусам и косинусам позволяет использовать символический метод, разработанный для анализа передачи гармонических колебаний через линейные цепи. Поэтому гармонический анализ получил широкое распространение во всех отраслях современной науки и техники.

Дата добавления: 2014-01-07