
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Спектральный анализ периодических сигналов
|
|
|
|
Математической моделью процесса, циклически повторяющегося во времени, является периодический сигнал. Если какой-либо сигнал представлен в виде суммы гармонических колебаний с различными частотами, то говорят, что осуществлено спектральное разложение этого сигнала в базисе гармонических функций. Сумма отдельных гармонических компонент сигнала образует его спектр.
Спектральное представление сигнала можно получить, используя разложение в ряд Фурье. Зададим на интервале времени [-T/2, T/2] полный ортогональный базис, образованный гармоническими функциями с кратными частотами:
{sin nw1t, cos nw1t}, n = 0, 1, 2,... (2.12)
Произвольный сигнал s(t) можно разложить на заданном интервале в ряд по тригонометрическому базису, т.е. получить его спектральное представление (2.5). Данное разложение справедливо на всей бесконечной оси времени и называется тригонометрическим рядом Фурье:
 (2.13)
(2.13)
где коэффициенты
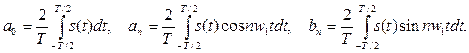 (2.14)
(2.14)
Если колебание представляет собой функцию, четную относительно t, т.е. s (t) = s(-t), то в тригонометрической записи ряда (2.13) остаются только косинусоидальные члены, т.к. коэффициенты bn в соответствии с формулой (2.14) обращаются в ноль. Для нечетной относительно t функции s(t), наоборот, в ноль обращаются коэффициенты an и ряд состоит только из синусоидальных членов.
Итак, в общем случае периодический сигнал содержит в себе не зависящую от времени постоянную составляющую, равную среднему значению сигнала на заданном интервале времени, и бесконечный набор гармонических колебаний, так называемых гармоник с частотами wn = nw1, n = 1, 2, 3,..., кратными основной частоте последовательности.
Любая гармоника ряда Фурье характеризуется амплитудой An и начальной фазой jn, которые соответственно называются амплитудной и фазовой характеристиками периодического сигнала. Для этого коэффициенты ряда следует записать в виде:
an = An cos jn; bn = An sin jn, а0/2 = А0;
так что 
Подставив эти выражения в (2.13), можно получить другую, эквивалентную форму ряда Фурье:
 (2.15)
(2.15)
которая иногда оказывается удобнее.
Графическое построение, наглядно интерпретирующее коэффициенты ряда Фурье для конкретного сигнала, называется спектральной диаграммой периодического сигнала. Различают амплитудные и фазовые диаграммы (рис. 2.1). Спектр периодической функции называется линейчатым или дискретным, т.к. состоит из отдельных линий, соответствующих дискретным частотам 0, w1, w2=2w1, w3=3w1 и т.д.
 An jn
An jn
0 w1 2w1 4w1 nw1 w 0 w1 2w1 4w1 6w1 w
a) б)
Рис. 2.1 – Спектральные диаграммы некоторого периодического сигнала:
а) - амплитудная; б) - фазовая
На практике чаще всего используют амплитудные диаграммы, позволяющие судить о процентном содержании тех или иных гармоник в спектре периодического сигнала.
Основную формулу спектрального анализа периодических сигналов (2.13) можно записать в ином симметричном виде, если воспользоваться представлением гармонических функций в виде суммы экспонент с мнимыми показателями, применяя формулы Эйлера или изначально используя экспоненциальный базис:
 (2.16)
(2.16)
Введем вместо an и bn новые коэффициенты Cn = (an - jbn)/2 для n = 1, 2, 3,.... Величины Cn можно определить и при отрицательных индексах n, причем С-n = (an + jbn)/2 = Cn*, т.е. является комплексно-сопряженной величиной по отношению к Cn, поскольку коэффициенты an и bn соответственно четны и нечетны относительно индексов. Таким образом, суммирование в (2.16) можно распространить на все значения n, положительные и отрицательные:
 (2.17)
(2.17)
Формула (2.17) является рядом Фурье в комплексной форме с коэффициентами:
 / Сn / = An/2. (2.18)
/ Сn / = An/2. (2.18)
Спектральная диаграмма периодического сигнала, представленного в форме (2.17), будучи симметричной относительно начала отсчета частоты, содержит компоненты на отрицательной полуоси частот, т.е. комплексный ряд есть продолжение или обобщение тригонометрического на эту область. Смысл понятия отрицательной частоты заключается в следующем. Вещественная функция (An cos nw1t) из (2.15) после применения формул Эйлера может быть выражена как сумма проекций на горизонтальную ось ОХ двух векторов длиной An/2 = Cn, вращающихся с угловой частотой nw1 во взаимно противоположных направлениях. Вектор, вращающийся против часовой стрелки, соответствует слагаемому (An/2)exp(jnw1t), т.е. положительной частоте, а вектор, вращающийся по часовой стрелке, слагаемому (An/2)exp(-jnw1t) и отрицательной частоте. Складываясь, эти два комплексных числа образуют вещественное число. Таким образом, отрицательная частота – понятие не физическое, а математическое, обусловленное способом представления комплексных чисел.
Таким образом, тригонометрический и комплексный ряды Фурье можно рассматривать как два равноценных (равноправных) способа представления одного и того же ряда. Для анализа периодических сигналов используется разложение их в ряд Фурье, являющееся основной характеристикой сигнала в частотной области и позволяющее построить АЧХ (функцию четную по частоте) и нечетную по частоте ФЧХ данного сигнала.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 859; Нарушение авторских прав?; Мы поможем в написании вашей работы!