Периодических и непериодических сигналов

Распределение энергии в спектрах

2.5.1 Пусть колебание s(t) (ток, напряжение) представляет собой сложную периодическую функцию времени с периодом Т. Энергия такого колебания, длящегося от t = -¥ до t = ¥, бесконечно велика, поэтому основной интерес представляет средняя мощность периодического колебания и распределение этой мощности между отдельными гармониками. Очевидно, что средняя мощность колебания, рассматриваемого на всей оси времени, совпадает с мощностью, средней за один период Т. Поэтому можно использовать формулу средней за период мощности (2.11), тригонометрический ортогональный базис и с учетом того, что c₀ = a₀/2 =А₀; c_n= A_n/2; интервал ортогональности – Т и норма базисных функций - Т^1/2, можно получить:

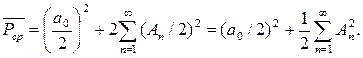(2.40)

Если s(t) представляет собой ток i(t), то при прохождении его через сопротивление r выделяется мощность (средняя):

где I₀ = a₀/2 – постоянная составляющая, а I_n = A_n – амплитуда n-й гармоники тока i(t).

Итак, полная мощность равна сумме средних мощностей, выделяемых отдельно постоянной составляющей I₀ и гармониками с амплитудами I₁, I₂,.... При этом можно определить мощность каждой из них в отдельности:

Это означает, что средняя мощность не зависит от фаз отдельных гармоник. Тогда энергия сигнала за период определится как Е = Р_ср *Т.

2.5.2 Для получения выражения, определяющего распределение энергии в спектре непериодического колебания, целесообразно воспользоваться результатами, полученными для произведения двух сигналов. Если u(t) и v(t) представляют собой одно и то же колебание u(t) = v(t) = s(t) (при этом w = 0, поскольку сдвиг между сигналами по частоте в силу их идентичности равен нулю), то интеграл, определяющий спектральную плотность произведения двух сигналов (2.37)

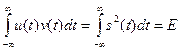
представляет собой полную энергию колебания s(t), а произведение спектральных плотностей из интеграла свертки (2.38) и свойства инверсии аргумента

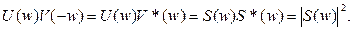
Таким образом, можно получить окончательный результат:

(2.41)

Это важное соотношение, устанавливающее связь между энергией колебания (при сопротивлении 1 Ом) и модулем его спектральной плотности, известно под названием равенства Парсеваля. Между выражениями (2.40) и (2.41) имеется существенное различие. В первом случае речь идет о средней мощности периодического колебания, где усреднение осуществляется делением энергии отрезка колебания за один период на величину Т. В случае же непериодического колебания конечной длительности усреднение энергии за бесконечно большой период дает нуль, и, следовательно, средняя мощность такого колебания равна нулю. Из выражения (2.41) видно, что квадрат модуля спектральной плотности, имеющую смысл энергии, приходящейся на единицу полосы частот, можно рассматривать как спектральную плотность энергии колебания.

Дата добавления: 2014-01-07