Особенности переходных процессов в цепях с одним реактивным элементом

В таких цепях характеристическое уравнение будет первого порядка. Получить это уравнение можно, например, так:

По способу Zвх(p)=0, при этом схемы могут иметь вид:

Рис (1) , ,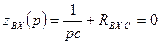

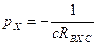Рис (2) , .

Видно, что корень характеристического уравнения получается отрицательным, т.е. с течением времени свободная составляющая .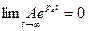

Ясно, что в разных схемах различными получаются величина А, величина , но свободная составляющая всегда будет иметь вид затухающей экспоненты. Для таких функций вводятся специальная характеристика.

Постоянная времени цепи (τ) – есть интервал времени, за который амплитуда свободной составляющей уменьшается в e раз.

Воспользовавшись этим определением, можно найти τ таким образом так как 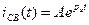, то

.

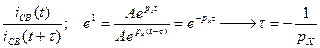В цепи: ,

т.е. τ зависит только от параметров рассматриваемой цепи (τ не зависит от начальных условий и напряжений источника).

Используя понятие τ, можно условно ввести понятие длительности переходного процесса. Так как 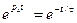, то

t	τ	3τ	5τ
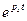
	0,36	0,05	0,004

В соответствие с этой таблицей принимают, что переходный процесс длится . К концу этого времени график переходного процесса практически сливается с принужденной составляющей.

Если известен график переходного процесса, из него можно найти τ.

Проще всего сделать так: на глаз определить, где кончается переходный процесс.

Длительность переходного процесса делят на 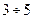. Это и будет τ.

- Из графика переходного процесса вычитают принужденную составляющую. Это будет график свободной составляющей. Задаются моментом времени t₁ и находят из графика x_св(t₁). Делят эту величину на e и получают x_св(t₁+ τ). Находят на графике эту величину, из нее определяют время t₂ и затем находят τ как τ = t₂ - t₁

- τ есть величина под касательной к графику переходного процесса. Подкасательная – это проекция на ось времени от точки, в которой проведена касательная до точки пересечения этой касательной с асимптотой.

Пример: Дано: 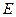, , . Найти i(t), u_c(t)

1) t<0

i(0_)=0, u_c(0_)=0,

2) t→∞

, ,

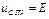Должен существовать переходной процесс, в течении которого от источника энергия передается к конденсатору, а по проводам идет ток, заряжающий конденсатор.

3) ,

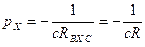
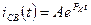4) ; ,

,

, ,

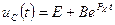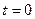
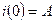5) Расчет начальных условий.

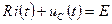
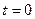
Тогда из получают

6)

,

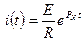
Пример: Дано: 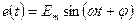, , 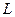. Найти .

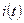1)

, ,

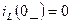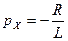2) Расчет принужденной составляющей.

В данном случае принужденный режим есть синусоидальный ток, поэтому расчет проведем символическим методом.

,

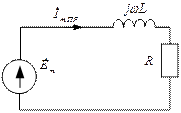
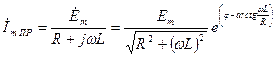
Переходят к мгновенному значению:

,

3) ; ,

4)

5)

6) ,

7)

,

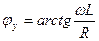
График проще всего построить по этапам:

1) принужденная составляющая;

2) exp соответствует свободной составляющей суммы этих графиков.

Дата добавления: 2014-01-07