Переходные процессы в цепях с двумя разнородными реактивными элементами

В этих цепях характеристическое уравнение имеет второй порядок, следовательно, будет два корня и две произвольные постоянные в свободной составляющей. Самое главное это то, что у квадратного уравнения есть 3 типа корней (вещественные различные, вещественные одинаковые и пара комплексно-сопряжённых), поэтому вид свободных составляющих в разных цепях получается различным. Рассмотрим возможные варианты на простейших примерах.

Пример:

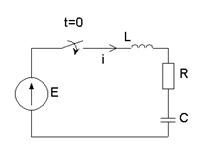
1) i_L(0_) = 0, u_c(0_)=0,

2) i _пр = 0, u_{R пр} = i_прR = 0

u_{C пр} = E, u_{L пр} = 0

3) Будем искать ток в цепи. Тогда надо иметь два начальных условия: i (0) и i ΄(0).

Для цепи после коммутации:

,

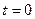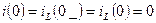
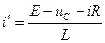
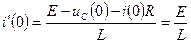
В данной схеме все 3 способа получения характеристического уравнения имеют одинаковую трудоёмкость.

, ,

,

.

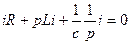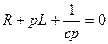В зависимости от величины подкоренного выражения получаются разные типы корней.

Если 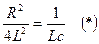, то подкоренное выражение равно нулю, и следовательно получим 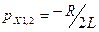. Из выражения (*) видно, что это получается при некотором «критическом» значении сопротивления .

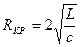Если же R > R_кр то подкоренное выражение положительно, и получим два вещественных различных корня. Если R < R_кр, под корнем будет отрицательное число, и получим пару комплексно сопряжённых корней.

1) R > R_кр (два вещественных различных корня) и тогда решение для тока запишется в виде:

,

,

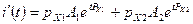и при t = 0 получаем два уравнения для расчёта произвольных постоянных:

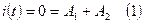
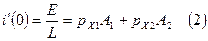
Из (1): 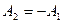, и подставляя в (2):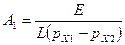

График проще построить по частям (принуждённая составляющая и каждое слагаемое свободной составляющей, а затем сложить).

Говорят, что это апериодический процесс.

Аналогично можно получить выражения и графики для напряжения на электродах:

2) R = R_кр

,

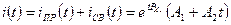
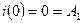при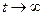

Графики имеют в этом случае точно такой же вид, как и в предыдущем случае, но в первом случае процессы идут медленнее, чем во втором. Этот случай называется критическим переходным процессом.

3) R < R_кр

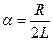, , т.е. при α→ 0 ω_c стремится к резонансной частоте данной цепи.

Решение запишется в виде:

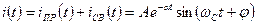(классический метод)

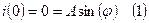
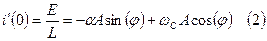
(1) в (2):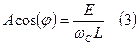

(1)/(3): 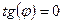, из (3)

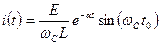
Видно, что в данном случае свободная составляющая представляет собой затухающую во времени синусоиду. Такой переходной процесс называется колебательным или периодическим, и график его проще построить так: симметрично относительно принуждённой составляющей строим график амплитуды свободной составляющей (график огибающей процесса), дальше в график огибающей вписывают синусоиду с её начальной фазой и периодом свободных колебаний.

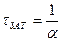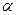, - коэффициент затухания,

- частота свободных колебаний.

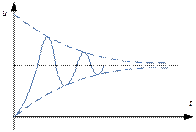
Рассматривать цепи более высокого порядка смысла нет, потому что у любого уравнения корни могут быть трёх видов, а для каждого типа корней мы свободную составляющую уже получили.

Дата добавления: 2014-01-07