Преобразование случайного сигнала линейным звеном

При воздействии стационарного случайного процесса на линейное устойчивое звено на выходе звена возникает также стационарный случайный процесс, который можно рассматривать как преобразованный входной сигнал.

Преобразование входного сигнала проявляется в изменении его статистических характеристик: математического ожидания, дисперсии, корреляционной функции и спектральной плотности.

Если входной сигнал – центрированный, то и выходной сигнал также будет центрированным. Далее рассматриваются центрированные сигналы (без обозначения их индексом в виде кружочка)

Для рассмотрения законов преобразования случайного сигнала вводятся характеристики, оценивающие связь между случайными сигналами: взаимнокорреляционная функция и взаимная спектральная плотность.

Взаимнокорреляционная функция стационарных случайных сигналов характеризует степень связи (корреляции) между мгновенными значениями сигналов и 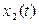, отстоящих друг от друга на величину 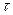. Взаимнокорреляционная функция определяется по формуле:

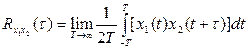(5.33)

Взаимнокорреляционная функция обладает следующими свойствами:

· Если сигналы и 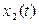не связаны (не коррелированны) между собой, то при взаимнокорреляционная функция будет равна нулю при любых :

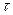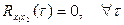(5.34)

· Взаимнокорреляционная функция обладает свойством:

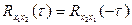(5.35)

· Если случайный процесс представляет собой сумму двух случайных процессов:

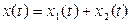, (5.36)

то взаимнокорреляционная функция имеет вид:

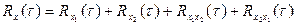(5.37)

В этом случае взаимнокорреляционная функция называется автокорреляционной функцией.

Если сигналы и 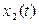не связаны (не коррелированны) между собой, то взаимнокорреляционная функция (автокорреляционная функция) определяется как:

(5.38)

Взаимная спектральная плотность стационарных случайных сигналов и 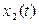определяется следующим образом:

(5.39)

Взаимная спектральная плотность имеет следующие свойства:

· Взаимная спектральная плотность является комплексной функцией и для нее справедливо следующее:

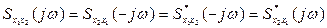, (5.40)

где * обозначены сопряженные функции.

· Если случайный процесс представляет собой сумму двух случайных процессов (5.36)

то взаимная спектральная плотность имеет вид:

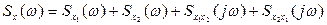(5.41)

Если сигналы и 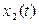не связаны (не коррелированны) между собой, то взаимная спектральная плотность определяется как:

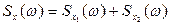(5.42)

Рассмотрим связь между статистическими характеристиками двух стационарных случайных процессов 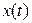и 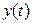, являющимися входным и выходным сигналами линейной динамической системы с передаточной функцией .

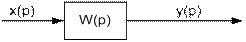
Рис. 5.18.

Наиболее просто определяется связь между математическими ожиданиями этих сигналов. Так как у стационарных сигналов математические ожидания являются постоянными величинами, то связь между ними определяется уравнением статики звена:

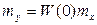(5.43)

Преобразование входного сигнала 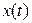в выходной сигнал 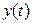можно рассматривать во временной и частотной областях.

Дата добавления: 2014-01-07