Доказательство. Построим таблицу истинности для формулы :

Построим таблицу истинности для формулы :

А	А
и	л	л
л	и	л

Столбец под самой пропозициональной формулой состоит только из букв «л», следовательно, формула – противоречие. (что и треб. доказать)

Теорема. Формула Д является тавтологией тогда и только тогда, когда (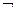 Д) есть противоречие. (без доказательства)

Замечания. 1. Противоречие и тавтология связаны друг с другом: отрицание противоречия есть тавтология и наоборот. 2. Связь между понятиями равносильности и эквивалентности: если формулы А и В равносильны (А = В), то формула – тавтология и обратно, если – тавтология, то формулы А и В равносильны.

Определение 26. Высказывание (в каком – нибудь естественном языке, вроде русского, или в каком-то искусственном языке), которое получается из какой-либо тавтологии посредством подстановки высказываний вместо пропозициональных букв, при условии, что вхождения одной и той же буквы замещаются одним и тем же высказыванием, называется логически истинным.

Пример. Рассмотрим предложение русского языка: «Если идет дождь или идет снег, и не идет снег, то идет дождь», которое можно получить подстановкой в тавтологию:

.

Задание: доказать самостоятельно, что это тавтология.

Определение 27. Высказывание, которое можно получить с помощью подстановки в противоречие, называется логически ложным.

Замечание. Существуют и такие виды логических рассуждений, которые не могут быть обоснованы в рамках исчисления высказываний. Корректность этих умозаключений покоится не только на истинностно–функциональных отношениях, но и на внутренней структуре самих предложений.

Например, утверждение: «Всякий друг Мартина есть друг Джона; Питер не есть друг Джона, следовательно, Питер не есть друг Мартина». Запишем это утверждение, предварительно обозначив через: m – Мартин, j – Джон, p – Питер, f (x,y) – предикат: f (x,y): x есть друг y. Тогда

, .

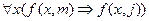Иногда записывают в виде: .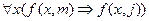

Дата добавления: 2014-01-07