
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Законы Кирхгофа в цепях синусоидального тока. Методы расчета цепей синусоидального тока
|
|
|
|
Способы задания синусоидального тока
Как следует из вышесказанного, синусоидальный ток можно задать четырьмя различными формами: уравнением i = Imsin(wt + y), определяющим мгновенное значение тока (значение тока в любой момент времени), волновой диаграммой, вектором и комплексным числом. При этом мы легко можем перейти от одной формы задания к другой.
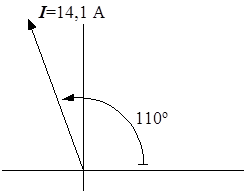 |
Например:
1) i = 20sin(wt+110°),
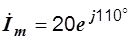 ,
,
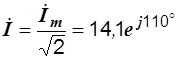 ;
;
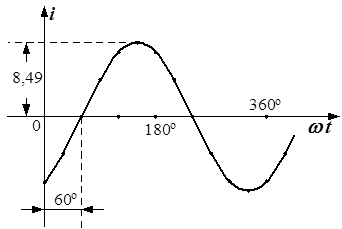 |
2) 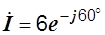 ,
,
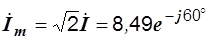 ,
,
i = 8,49sin(wt-60°);
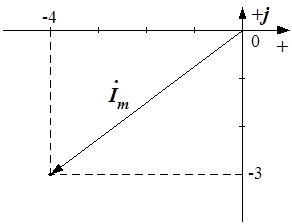 |
3) 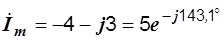 ,
,
i = 5sin(wt-143,1°),
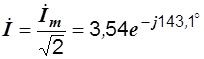 ,
,
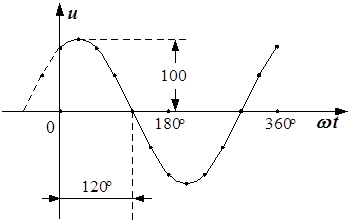
u = 100 sin ( wt + 60° ).
В качестве начальной фазы мы берем не 120°, которые указаны на волновой диаграмме, а тот угол, на который сдвинуто начало синусоиды. Начальная фаза на волновой диаграмме определяется ближайшей к началу координат точкой перехода синусоиды через ноль от минуса к плюсу – это 60°. Так как начало синусоиды смещено от точки 0 влево, то начальная фаза положительна.
Для мгновенных значений ЭДС, токов и напряжений остаются справедливыми сформулированные ранее законы Кирхгофа.
П е р в ы й: в любой момент времени алгебраическая сумма токов в узле электрической цепи равна нулю:
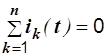 , (2.8)
, (2.8)
где n – число ветвей, сходящихся в узле.
В т о р о й: в любой момент времени в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех остальных элементах контура:
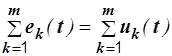 , (2.9)
, (2.9)
где m – число ветвей, образующих контур.
Токи, напряжения и ЭДС, входящие в уравнения (2.8) и (2.9), есть синусоидальные функции времени, которые мы рассматриваем как проекции некоторых векторов на оси координат. Так как сложению проекций соответствует сложение векторов и соответствующих им комплексных чисел, то справедливыми будут следующие уравнения, которые можно записывать как для действующих, так и для амплитудных значений.
| Законы Кирхгофа в векторной форме: | Законы Кирхгофа в символической форме: |
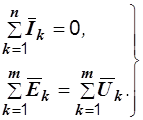 (2.10) (2.10)
| 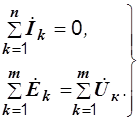 (2.11) (2.11)
|
Из сказанного вытекают три возможных подхода к расчету цепей синусоидального тока: выполнение операций непосредственно над синусоидальными функциями времени по уравнениям (2.8) и (2.9); применение метода векторных диаграмм, основанного на уравнениях (2.10), использование в расчетах комплексных чисел и уравнений (2.11), являющихся основой символического метода.
Пример 2.4. В узле электрической цепи сходятся три ветви
(рис. 2.14).
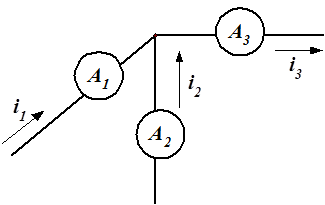 Рис. 2.14. Узел электрической цепи
Рис. 2.14. Узел электрической цепи
|
Токи первых двух ветвей известны:
i1 = 8sin(wt+30°) А,
i2 = 6sin(wt+120°) А.
Требуется записать выражение тока i3 и определить показания амперметров электромагнитной системы.
Р е ш е н и е. 1. Непосредственное сложение синусоид:
i3 = i1+i2 = 8sin(wt+30°)+6sin(wt+120°) = I3msin(wt+y3).
Сумма двух синусоид одинаковой частоты есть тоже синусоида той же частоты. Ее амплитуда и начальная фаза могут быть найдены по известным из математики формулам:
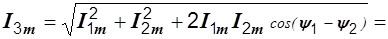
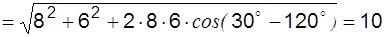 A,
A,
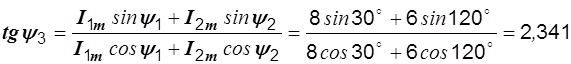 ,
,
откуда y3 = 66,87°. Итак, i3 = 10 sin ( wt+66,87° ).
2. Применение метода векторных диаграмм.
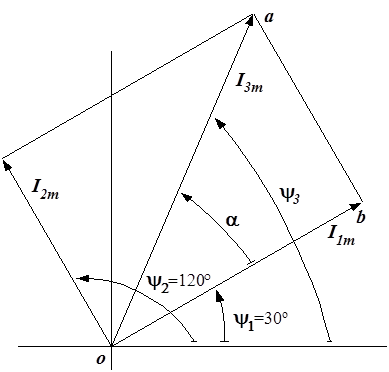 Рис. 2.15. Векторная диаграмма токов
Рис. 2.15. Векторная диаграмма токов
|
В соответствии с первым законом Кирхгофа в векторной форме для цепи на рис. 2.14 имеем 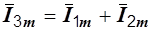 . В прямоугольной системе координат строим векторы
. В прямоугольной системе координат строим векторы  и
и 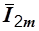 и находим вектор
и находим вектор 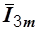 , равный их сумме (рис. 2.15).
, равный их сумме (рис. 2.15).
Так как треугольник oab прямоугольный, а сторона ab равна длине вектора I2m, то 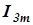 =
= 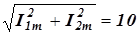 А.
А.
Если треугольник получается не прямоугольным, то применяется теорема косинусов.
Начальная фаза третьего тока равна углу наклона: вектора I3m к горизонтальной оси:
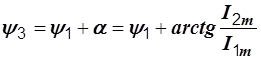
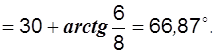
3. Решение символическим методом.
Записываем комплексные амплитуды первого и второго токов:
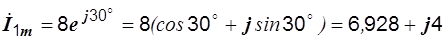 A,
A,
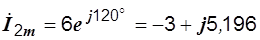 A.
A.
По первому закону Кирхгофа в символической форме
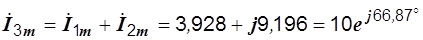 А.
А.
Модуль последнего комплексного числа равен амплитуде третьего тока, а аргумент – начальной фазе.
Определяем показания амперметров. Приборы электромагнитной системы показывают действующие значения токов и напряжений, поэтому
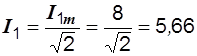 A,
A, 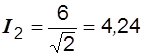 A,
A, 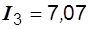 A.
A.
Обращаем внимание на то, что 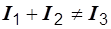 . Это не ошибка. В цепях синусоидального тока для показаний приборов законы Кирхгофа не справедливы. Можно складывать мгновенные значения токов (синусоидальные функции времени), векторы и комплексные числа, но не численные значения токов и напряжений, не показания приборов.
. Это не ошибка. В цепях синусоидального тока для показаний приборов законы Кирхгофа не справедливы. Можно складывать мгновенные значения токов (синусоидальные функции времени), векторы и комплексные числа, но не численные значения токов и напряжений, не показания приборов.
Следует заметить, что первый из рассмотренных в примере методов из-за громоздкости вычислительных операций с синусоидами практически не применяется.
Метод векторных диаграмм удобен при решении относительно несложных задач.
В символической форме, как будет показано ниже, можно рассчитать сколь угодно сложную линейную цепь.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 9159; Нарушение авторских прав?; Мы поможем в написании вашей работы!