Методы разработки алгоритмов

Тема 5.

Существует достаточно большое число методов разработки эффективных алгоритмов решения задач различных классов.

Наиболее часто используются следующие методы:

1) «Разделяй и властвуй» - метод декомпозиции, метод сведения задачи к подзадачам, метод частных целей.

2) Балансировка. Этот метод применим только к алгоритмам, к которым уже применялся 1-ый метод.

3) Динамическое программирование.

4) «Жадный» алгоритм.

5) Метод программирования «с отходом назад» (Back Tracing), программирование с отслеживанием.

6) Метод локального поиска.

7) Метод подъема.

8) Метод эвристики.

9) Метод рекурсии.

10) Моделирование задач.

5.1 Метод «Разделяй и властвуй».

При решении задачи необходимо ответить на следующие вопросы:

1. Известно ли решение для какой-либо части задачи и можно ли решить оставшуюся неизвестной часть.

2. Известны ли частные случаи решения задачи, и можно ли разработать алгоритм решения задачи для ограниченного подмножества исходных операндов.

3. Существует ли в задаче неясные моменты (раскрытие глубины задачи).

4. Существует ил похожая задача того же класса и решение для нее. Можно ли изменить алгоритм решения второй задачи для получения решения первой.

В основе метода «Разделяй и властвуй» лежит разбиение задачи на подзадачи (декомпозиция).

Первый шаг – это разделение задачи на К подзадач со сложностью 1/К.

Властвование – второй шаг алгоритма. Это – использование рекурсионного процесса разбиения подзадач на еще более мелкие подзадачи до тех пор, пока подзадачи n-го уровня разделения будут достаточно малы для их тривиального решения.

… … … …

Третий этап метода – склеивание множества решений отдельных подзадач в общее решение.

Использование этого метода требует, чтобы в процессе разбиения подзадачи не повторялись и не пересекались друг с другом. Если это условие не выполняется, то данный метод решения не применим к таким задачам.

Примерами решаемых этим методом задач являются:

ü сортировка слиянием;

ü нахождение максимального/минимального элемента массива;

ü умножение длинных целочисленных значений;

ü алгоритм быстрого преобразования Фурье;

ü алгоритм «Ханойская башня»;

ü составление графика проведения чемпионата.

Задача 5.1.1

Отсортировать массив из n чисел в порядке возрастания.

Обменная сортировка:

1 итерация

2 итерация

3 итерация

Общая формула временной сложности записывается рекуррентно:

T(n)=n*(n-1)/2=O(n²)

Приведенный алгоритм построен на основе метода «Разделяй и властвуй».

Недостаток: в приведенном алгоритме размеры подзадач на каждой итерации одинаковы, поэтому при больших n этот алгоритм неэффективен.

Для повышения эффективности алгоритмов, разработанных методом «Разделяй и властвуй», используется метод балансировки, который заключается в разбиении задачи на подзадачи равных размеров.

Например:

Алгоритм сортировки слиянием.

6

Вычислительная сложность этого алгоритма:

T₂(n)=O(n*log(n)),

поэтому можно сделать вывод, что данный алгоритм также является рекурсивным.

Пример процедуры, реализующей этот алгоритм:

Procedure JointSort(P, R: integer;

var A, B: TArray);

var q: integer;

begin

if P=R then exit;

q:= (P+R) div2;

JointSort(P, q, A, B);

JointSort(q+1, R, B, A);

JointSort(P, q, R, B, A);

end;

Метод «Разделяй и властвуй» полезен, если задачу можно разбить на подзадачи за приемлемое время, а суммарный размер подзадач будет небольшим.

Если сумма размеров подзадач пропорциональна a*N, где а=const (a>1), то этот метод дает алгоритм с полиномиальной сложностью O(N^m).

Если разбиение задачи размером N приводит к N подзадачам, каждая из которых имеет сложность (N-1), то такой алгоритм будет иметь экспоненциальную сложность O(m^N).

Задача 5.1.2

Составление сетевого графика выполнения работ.

Имеется комплекс взаимосвязанных работ N. Для каждой из работ задана трудоемкость выполнения. Имеется К рабочих. Требуется распределить рабочих по операциям таким образом, чтобы длительность выполнения всего комплекса работ была минимальной.

Примечание: не учитываются субъективные факторы, и невозможно перемещение рабочих с одной операции на другую в процессе выполнения.

Комплекс взаимосвязанных работ представляется в виде сетевого графика, где узлы графа – это события окончания предшествующих работ, дуги – работы.

Трудоемкость R_i,j характеризует затраты ресурсов на выполнение работы.

Пример сетевого графика:

L(0, М) – длительность выполнения работы. Эта величина определяется как совокупность возможных путей в графе

{I₁, I₂, I₃}

В данном примере возможны 3 маршрута:

I₁={(0, 1); (1, 3); (3, 5)}

I₂={(0, 1); (1, 4); (4, 5)}

I₃={(0, 2); (2, 4); (4, 5)}

I₁=1+2+4=7 – «критический» путь I_кр.

I₂=1+2+1=4

I₁=2+3+1=6

Необходимо расставить по операциям заданное число рабочих.

Для случая, когда K=N задача является тривиальной.

Для K¹N имеется N^(K-N) возможных вариантов расстановки.

Пусть N=7, К=10, тогда имеется 1296 вариантов размещения рабочих.

Решение этой задачи методом полного перебора вариантов неэффективно.

Используя метод «Разделяй и властвуй», разбивают исходную задачу на (К-N) последовательных подзадач. Затем решают вопрос о том, на какую операцию поставить 1-го свободного рабочего (для данного примера – 8-го рабочего). После этого размещают 2-го свободного рабочего, взяв за исходное ранее найденное решение и т.д.

Каждая из этих подзадач может быть сформулирована следующим образом: необходимо принять решение о добавлении одного работника на одну из работ комплекса, чтобы полученная расстановка минимизировала «критический» путь

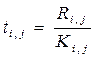
Свободного рабочего размещают на одну из работ, входящих в «критический» путь, желательно, наиболее трудоемкую (здесь – (3, 5)).

Тогда получаем:

I₁’=1+2+4/2=5 ® I₃=6 ® I_кр

L(0, 5)=6

Поиск решения данным алгоритмом требует анализа не более N*(K-N) вариантов.

Дата добавления: 2014-01-07