Метод подъема или метод локального поиска

Примеры задач, решаемых этим методом:

1) Задача сетевого планирования.

2) Задача нахождения максимума функции нескольких переменных.

3) Задача поиска минимального остовного дерева в графе.

4) Задача коммивояжера.

5) Алгоритмы численных методов, дающие приближенные решения.

6) Задачи линейного программирования

и др.

Данный метод начинает работу с принятия начального предположения или вычисления начального решения задачи (1 этап).

2 этап – быстрое восхождение вверх от начального решения к более лучшим решениям. Восхождение заключается в преобразовании исходного решения по некоторой заданной ограниченной совокупности решений.

3 этап – перебор всех решений из ограниченного множества до тех пор, пока не будет найдено решение, улучшить которое невозможно. Однако найденное решение может быть неоптимальным (приближенным).

Примечание: если рассматривать улучшение начального решения на множестве всех возможных решений, то получаем метод полного перебора вариантов, дающий оптимальное решение за время, которое может быть неприемлемым. Поэтому метод подъема рассчитан на ограниченное подмножество решений, перебор которых дает вычислительную сложность порядка O(n²) или O(n³).

Метод подъема не гарантирует нахождение оптимального решения за один раз. Если задать несколько начальных приближений и найти соответствующие локальные оптимальные решения, которые могут различаться, и сравнить найденные максимумы с некоторой стоимостной функцией, то можно найти глобальное оптимальное решение.

Определим, как действует метод подъема для задачи сетевого планирования, рассмотренной в предыдущем пункте.

1 шаг – задается начальное решение Z₀ (начальная расстановка всех 10 рабочих по семи операциям).

2 шаг – свободное число рабочих размещается по следующей схеме:

1. Ставится один рабочий на работу с максимальной трудоемкостью. Эта работа может не принадлежать «критическому» пути.

2. Если есть свободные рабочие, то они размещаются на работы с максимальной трудоемкостью до тех пор, пока все рабочие не будут расставлены.

Пример:

Пусть К₀₁=1, К₀₂=2, К₁₃=1, К₂₄=2, К₃₄=2, К₁₄=1, К₄₅=1.

T(I₁)=t₀₁+ t₁₃+ t₃₅=1/1+2/1+4/2=5= I_кр

T(I₂)=t₀₁+ t₁₄+ t₄₅=1/1+2/1+1/1=4

T(I₃)=t₀₂+ t₂₄+ t₄₅=2/2+3/2+1/1=3,5

Берут рабочего с работы, не принадлежащей «критическому» пути, и ставят на другую работу, которая принадлежит «критическому» пути. Затем анализируют время выполнения всего комплекса работ. Если найдено улучшение, то процесс повторяют до тех пор, пока окажется, что любые перемещения не приводят к улучшению решения.

Условия перемещения рабочих:

1)

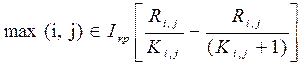
2) Нельзя снимать рабочих с работ, для которых K_i,j=1.

Для заданного примера (0, 2)Ú(2, 4)

(1, 3) ® max[(1/1 - 1/2); (2/1 - 2/2); (4/2 - 4/3)]

Затем проводят перестановку рабочего и пересчитывают длительность выполнения работ на пути.

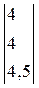
Для рассмотренного примера можно показать, что найденное решение является наилучшим.

5.3 Метод «Жадный алгоритм».

«Жадный алгоритм» позволяет получить оптимальный результат в целом. Однако в жизни «жадная» стратегия дает стоимостную выгоду, тогда как общий результат может оказаться неприемлемым.

Примеры «Жадных алгоритмов»:

1) Алгоритм Крускала поиска минимального остовного дерева.

2) Алгоритм Дейкстра поиска кратчайшего пути в неориентированном графе.

3) Модифицированный алгоритм Крускала для задачи коммивояжера.

Задача 5.3.1

Нахождение минимального остовного дерева.

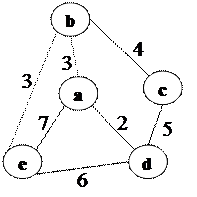S₀=7+4+4+5=20

S₁=19

S₂=16

S₃=13

S₄=12

Получаем минимальное остовное дерево:

«Жадный алгоритм» сначала рассматривает все «свободные» дуги, выбирает дугу с минимальной стоимостью и добавляет ее к остовному графу. При этом получается цикл acd. Затем просматривает все дуги, входящие в цикл, и убирает дугу с максимальной стоимостью.

5.4 Метод программирования «с отходом назад» (Back Tracing).

Этот метод (называемый еще методом «поиска с возвратом») позволяет выполнить исчерпывающий поиск требуемого решения задачи без перебора всех возможных вариантов.

Примеры задач, в которых используется данный метод:

1) Поиск кратчайшего пути в графе.

2) Выход из лабиринта.

3) Обход шахматной доски конем.

4) Задача о восьми ферзях.

5) Крестики-нолики.

6) Пятнашки.

7) Задача коммивояжера.

Алгоритмы «поиска с возвратом» наиболее часто представляются в виде рекурсий. Эти алгоритмы ищут решение методом проб и ошибок, перебирая все или почти все варианты, поэтому их называют «лобовыми» алгоритмами. Такие алгоритмы наименее эффективны, чем другие.

Алгоритмы «поиска с возвратом» используются в случаях, когда нельзя применить другие, более эффективные алгоритмы. Поэтому «поиск с возвратом» - это метод на крайний случай. Он всего на один порядок лучше, чем прямой перебор всех вариантов.

Работа алгоритмов «с отходом назад» начинается от искомой цели и движется по направлению к постановке задачи с проверкой условий. При этом возможен обратный возврат от постановки задачи к решению.

Сложность алгоритмов «с возвратом» в худшем случае экспоненциальная, когда для поиска решения приходится просмотреть все варианты.

Общий принцип построения алгоритмов «поиска с возвратом»:

1 шаг: Задается начальное состояние,

2 шаг: Строится дерево решений, возможных для каждого состояния задачи,

3 шаг: Задается целевая функция стоимости решений,

4 шаг: Производится обход дерева с проверкой целевой функции для каждого решения и возвратом назад в корневую вершину с исключением пройденных ветвей дерева.

В результате прохождения графа будет найдено оптимальное решение.

Примечание: Для некоторых задач алгоритм «поиска с возвратом» не требует просмотра всех вариантов, что дает единственно правильное решение.

Задача 5.4.1

Задача обхода шахматной доски конем.

Целевая функция здесь определяет, свободна или занята одна из возможных клеток для последующего хода. Если все возможные решения являются занятыми клетками, то происходит возврат назад и выбор другого варианта решения.

При этом для многих алгоритмов «поиска с возвратом» в дереве всегда выбирают сначала левую ветвь поиска.

Задача 5.4.2

Задача о велосипедном замке.

Замок состоит из N переключателей. Он сработает в том случае, если совпадет кодовая комбинация, в которой не менее N/2 переключателей включены.

Исходя из условия, следует, что множество решений разбиваются на 2 подмножества А и В, где А – правильные решения, В – решения, противоречащие условию.

Количество возможных комбинаций определяется как 2^N.

При N £ 10 алгоритм полного перебора дает 2¹⁰=1024 комбинации.

При N > 10 время поиска растет экспоненциально.

Procedure Code(N: integer);

var i: integer;

j, K: longint;

begin

K:=1;

for j:=1 to N do K:=K*2;

for j:=1 to K do

{проверка совпадения кода}

end;

Если учитывать условие задачи, то из рассмотрения можно исключить большую часть вариантов решения.

Построим дерево решений для алгоритма «поиска с возвратом» при N=4.

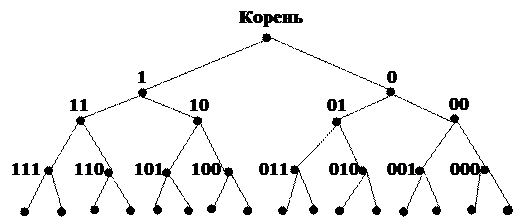2⁴=16 комбинаций

16-5=11 возможных решений

Движение вниз по дереву выполняется по левой ветви. На последнем уровне проверяется комбинация. Если замок не открылся – возвращаемся на один уровень вверх и спускаемся по другой, самой левой из нерассмотренных ветвей и т. д.

Примечание: Алгоритмы «поиска с возвратом» в худшем случае перебирают все возможные варианты, хотя существуют модификации этого метода, позволяющие существенно сократить область поиска.

К ним относят:

ü метод ab-отсечений;

ü метод ветвей и границ;

ü использование эвристик, дающих приближенное решение за короткое время, которое принимается за начальное состояние в алгоритме «поиска с возвратом» для поиска точного решения.

Задача 5.4.3

Игра «Пятнашки».

Зададим сначала приоритет ходов:

1) ¬

2) ­

3) ®

4) ¯

Дерево решений для алгоритма «с возвратом назад»:

2

Дата добавления: 2014-01-07