Эвристики

Эвристический алгоритм обладает следующими свойствами:

a) Он дает хорошее, хотя и не всегда оптимальное решение.

b) Он работает быстрее и его проще реализовать, чем любой точный алгоритм.

Хотя не существует универсальной структуры, описывающей эвристические алгоритмы, многие из них основаны на других методах:

o «Разделяй и властвуй»;

o подъема;

o обратного отслеживания.

Общий подход к построению эвристических алгоритмов заключается в перечислении всех требований к точному решению и их разделению на два класса:

1. Первый класс включает требования, которые легко удовлетворить.

2. Второй класс включает требования, которые удовлетворить нелегко.

Иными словами, первый класс – это требования, которые обязательно должны быть удовлетворены. Второй класс – требования, по отношению к которым допускается компромисс.

В этом случае цель построения эвристического алгоритма заключается в создании алгоритма, который гарантирует выполнение требований первого класса, и который мог бы выполнить требования второго класса, однако гарантии этому нет.

Часто очень хорошие алгоритмы должны рассматриваться как эвристики. Например, алгоритм, который хорошо работает на всех тестовых задачах, считается эвристикой, пока не будет найдено доказательство его правильности.

Задача 5.5.1

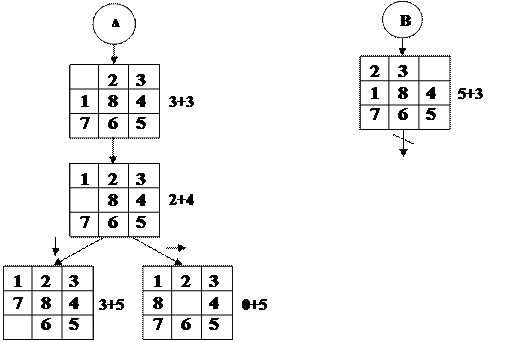
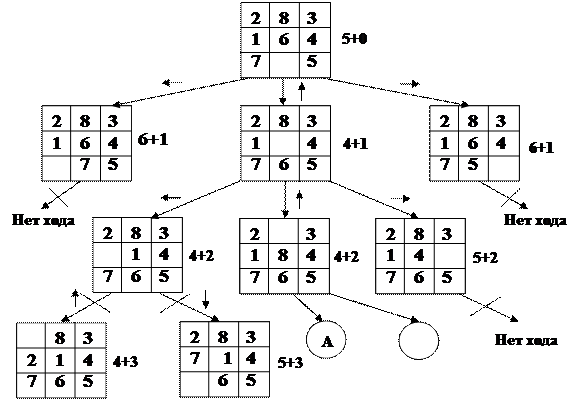
Рассмотрим использование эвристического алгоритма на примере игры «Пятнашки».

Эвристика определяется по формуле

H=D+L,

где D – число неупорядоченных фигур;

L – уровень дерева.

В

Здесь L определяет также число шагов, за которое будет найдено оптимальное решение.

Приведенный алгоритм реализует поиск «в ширину», т. е. рассматриваются альтернативы на одинаковом уровне, а критерий выбора альтернативы – целевая функция, задаваемая эвристикой.

Рассмотренный эвристический алгоритм ведет себя как «Жадный алгоритм». Разница заключается в том, что здесь критерий оптимальности мы задали сами.

Задача 5.5.2

Задача коммивояжера.

Задан граф связанных городов со стоимостью проезда между городами. Необходимо построить замкнутый путь, связывающий все вершины друг с другом и обладающий минимальной стоимостью.

S=

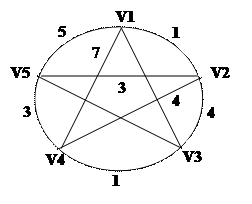
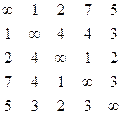
Тур 1: 1 – 5 – 3 – 4 – 2 – 1

S1=13

Рассмотрим «Жадный алгоритм» нахождения минимального пути.

Tour=0

C=0

V=V1

V=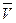

V - текущее время;

V1 – начальное время;

С – стоимость.

1 шаг: Посещение всех городов

for k=1 to N-1 do

2 шаг: Выбираем следующий город W. Далее выбираем ребро, которое при присоединении дает минимальную стоимость.

W, (V, W)=min

Tour=Tour+(V, W)

C=C+C_VW

3 шаг: После прохождения цикла

Tour=Tour+(V, U)

получаем следующий путь: 1 – 2 – 5 – 3 – 4 – 1

U=1 C₃=1+3+2+1+7=14

Недостаток: на первых итерациях всегда используется ребро с минимальной стоимостью, зато на последних – с максимальной стоимостью.

«Жадный алгоритм» является простым, но не дает оптимального решения. Однако его можно рассматривать как эвристику с учетом следующих положений:

1. Эвристический алгоритм задачи коммивояжера основан на методе подъема с целью нахождения минимального тура.

2. Задача сводится к набору частных целей: найти на каждом шаге самый дешевый город для следующего посещения.

3. Алгоритм не строит плана. Кроме того, в нем нет возврата назад.

4. Оптимальное решение обусловлено двумя основными условиями:

ü множество ребер вместе образует тур без циклов;

ü стоимость тура минимальна по сравнению с другими.

Для эвристического алгоритма свойство 1 является обязательным, а свойство 2 – трудным, что не гарантирует поиск минимума.

Для произвольной задачи с n вершинами требуется сложность алгоритма порядка O(n²), чтобы прочесть матрицу стоимости |S|. Следовательно, можно показать, что для реализации алгоритма требуется не более n² операций.

Вывод: Эвристический алгоритм решения задачи коммивояжера настолько эффективен, насколько это возможно, и является самым лучшим и широко используемым для больших городов W.

С целью повысить вероятность выполнения условия 2, возможны следующие способы модификации эвристических алгоритмов:

1) Применение алгоритма для любых p£n случайно выбранных городов.

2) Если зададим n=3, то Tour=3 – 4 – 5 – 2 – 1 – 3,

C₄=1+3+3+1+2=10, тогда сложность будет кратна O(pn²).

Если зададим n=3, то в качестве ближайшего города n второй наименьший по стоимости изменяющийся W=3.

Кроме того, можно задать ситуацию, когда рассматривается несколько туров и сохраняется минимальный на некотором шаге. Затем рассматривается следующий тур, определяется стоимость асимметричного графа и сравнивается с минимальной стоимостью. Если она больше, то прекращают движение по пути.

Дата добавления: 2014-01-07