
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие и значение природопользования, его социально-экономическая сущность
По направлению радиус-вектора точки М;
По сравнению биссектрисы 1-го координатного угла;
3)по направлению вектора 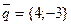
Производной функции U(M) по направлению 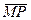 называют предел отношения разности
называют предел отношения разности 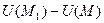 к величине направленного отрезка
к величине направленного отрезка 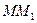 , когда точка
, когда точка 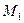 стремится к точке М, оставаясь на прямой МР.
стремится к точке М, оставаясь на прямой МР.
Производная функция U направлению 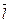 обозначается
обозначается  или
или 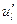 :
:

И вычисляется по формуле: 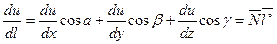 , где
, где
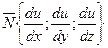 - нормальный вектор к поверхности уровня,
- нормальный вектор к поверхности уровня,
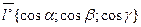 - единичный вектор направления
- единичный вектор направления 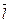
Производная  определяет величину скорости изменения функции U(M)при перемещении М по направлению
определяет величину скорости изменения функции U(M)при перемещении М по направлению  .
.
В каждой точке, где функция дифференцируемая, она имеет производную по любому направлению.
Производные функции U(x,y,z) по положительным направлениям осей координат 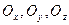 равны ее частным производным:
равны ее частным производным: 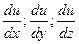
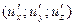 . Производные по прямо противоположным направлениям отличаются только по признаку.
. Производные по прямо противоположным направлениям отличаются только по признаку.
Производная функция U(х,у) по направлению линии уровня (касательному к линии уровня) и производная функции U(x,y,z) по направлению любой линии, лежащей на поверхности уровня (по левому направлению, касательному к поверхностью уровня), равны нулю.
Решение:
Находим частные производственные функции U и вычисляем их значение в точке М.
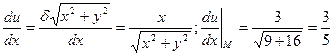
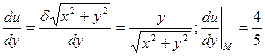
Подставляя в формулу 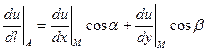
Находим далее косинусы углов 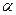 и
и  , образованных заданным направлением дифференцирования с осями координат, и производную функции U по заданному направлению:
, образованных заданным направлением дифференцирования с осями координат, и производную функции U по заданному направлению:
1)Для биссектрисы 1-го координатного угла: 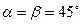 ,
, 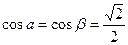 ,
, 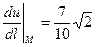 ;
;
2)Для радиус-вектора точки М: 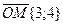 ,
, 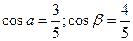 ,
, 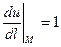 ;
;
3)Для вектора 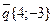 ,
, 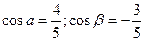 ,
, 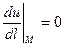 .
.
10. По справочным данным: для вакуума 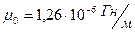 ,
, 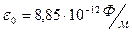 ; для воздуха
; для воздуха 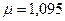 ,
, 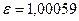 .
.
Определить скорость света в вакууме и скорость света в воздухе.
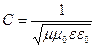 (
(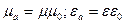 )
)
11. Составьте сравнительную таблицу единиц измерения основных электрических и магнитных величин. (Выразите их только через 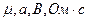 )
)
| Электрические величины | Магнитные величины |
Количество электричества (q)
Кл (Кулон) ~ 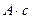 Напряжение, Э.д.с (U) В (Вольт)
Напряженность электрического поля (Е) В/м
Емкость (С) Ф (Фарада) ~ c/Ом
Абсолютная диэлектрическая проницаемость (
Напряжение, Э.д.с (U) В (Вольт)
Напряженность электрического поля (Е) В/м
Емкость (С) Ф (Фарада) ~ c/Ом
Абсолютная диэлектрическая проницаемость (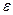 ) Ф/м ~ ) Ф/м ~ 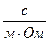
| Магнитный поток (Ф)
Вб (Вебер) ~ 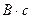
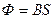 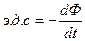 Магнитная индукция (В)
1Тл (Тесла) ~
Магнитная индукция (В)
1Тл (Тесла) ~ 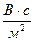 Напряженность магнитного поля (Н)
1А/м
Индуктивность Гн (Генри)
Напряженность магнитного поля (Н)
1А/м
Индуктивность Гн (Генри) 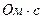 Абсолютная магнитная проницаемость (
Абсолютная магнитная проницаемость (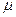 ) Гн/м ~ ) Гн/м ~ 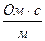
|
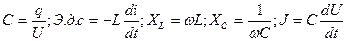
12. Найти поток векторного поля 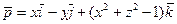 через поверхность эллипсоида
через поверхность эллипсоида 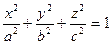 изнутри этой поверхности.
изнутри этой поверхности.
Векторным полем называется плоская или пространственная область, с каждой точкой М которой связано определенное значение некоторой физической величины 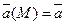 .
.
Если векторное поле отнесено к прямоугольной системе координат ОXYZ, то вектор будет векторной функцией, а его 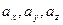 проекции на оси координат будут скалярными функциями от переменных x,y,z:
проекции на оси координат будут скалярными функциями от переменных x,y,z:
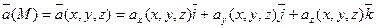
Поэтому задание поля векторной величины равносильно заданию трех скалярных (числовых) функций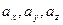 .
.
Потоком векторного поля, образованного вектором 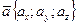 через поверхность называется поверхностный интеграл (скаляр)
через поверхность называется поверхностный интеграл (скаляр)
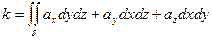 (1)
(1)
Если вектор 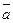 определяет поле скоростей текущей жидкости, то интеграл k выражает количество жидкости, протекающей через поверхность
определяет поле скоростей текущей жидкости, то интеграл k выражает количество жидкости, протекающей через поверхность 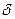 за единицу времени. При этом если
за единицу времени. При этом если 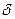 –замкнутая поверхность, ограничивающая область Q и если интеграл (1) берется по внешней стороне
–замкнутая поверхность, ограничивающая область Q и если интеграл (1) берется по внешней стороне 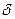 , то величина k называется потоком вектора
, то величина k называется потоком вектора 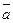 изнутри поверхности; она дает разность между количеством жидкости, вытекающей из области Q и втекающей в эту область за единицу времени (предполагается, что жидкость может свободно протекать через поверхность
изнутри поверхности; она дает разность между количеством жидкости, вытекающей из области Q и втекающей в эту область за единицу времени (предполагается, что жидкость может свободно протекать через поверхность 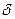 )
)
При k>0 из области Q вытекает жидкость больше, чем в нее втекает, что указывает на наличие в этой области источников, питающих поток жидкости. При k<0 из области вытекает жидкости меньше, чем втекает, что означает наличие в этой области стоков, где жидкость удаляется из потока. При k=0 из области вытекает жидкости столько же, сколько и втекает.
Решение Согласно (формуле 1)
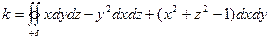
Расчленяем этот поверхностный интеграл на три слагаемых интеграла и, пользуясь данным уравнением эллипсоида 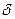 , сводим их вычисления к вычислению двойных интегралов.
, сводим их вычисления к вычислению двойных интегралов.
1) 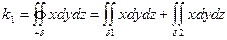
где 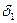 и
и 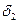 – части данного эллипсоида, расположенные по разные стороны от плоскостей yoz
– части данного эллипсоида, расположенные по разные стороны от плоскостей yoz
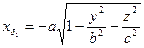 и
и 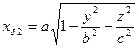
Преобразуя эти поверхностные интегралы в двойные, получим:
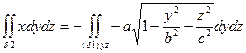
т.к. поверхность 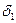 обращена в сторону отрицательного направления оси ox
обращена в сторону отрицательного направления оси ox
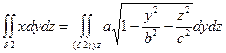
т.к. поверхность  обращена в сторону положительного направления ox.
обращена в сторону положительного направления ox.
Проекции 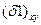 и
и 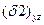 поверхностей
поверхностей  и
и  на плоскость yoz представляет один и тот же эллипс.
на плоскость yoz представляет один и тот же эллипс.
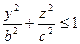
Поэтому:
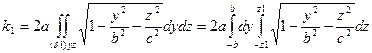
Где  – положительное значение z из уравнения эллипса
– положительное значение z из уравнения эллипса
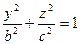
вычисляя двукратный интеграл, найдем
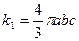
2) 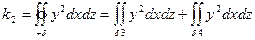
где  и
и  – части поверхности, расположенные по разные стороны от плоскости xoz, уравнения которых:
– части поверхности, расположенные по разные стороны от плоскости xoz, уравнения которых:
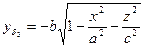 и
и 
Преобразуя поверхностные интегралы в двойные, получим
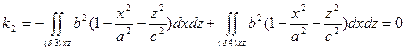
т.к. проекции 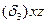 и
и  поверхностей на плоскость xoz одинаковы.
поверхностей на плоскость xoz одинаковы.
3) По аналогичной причине вследствие четности подынтегральной функции поверхностного интеграла 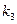 и симметричности поверхности
и симметричности поверхности 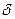 относительно плоскости xoy
относительно плоскости xoy
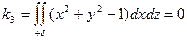
окончательно
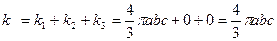
13 Найти дивергенцию векторного поля:
1) 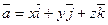 ; 2)
; 2) 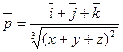 ; 3)
; 3) 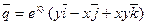 ;
;
Дивергенцией векторного поля, определяемого вектором, называют скаляр
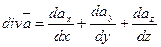 (2)
(2)
Если 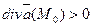 , то точку Мо называют источником, а если
, то точку Мо называют источником, а если 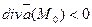 , то Мо называют стоком, ибо в первом случае в любой бесконечно малой области, окружающей точку Мо, жидкость возникает, а во втором случае она исчезает.
, то Мо называют стоком, ибо в первом случае в любой бесконечно малой области, окружающей точку Мо, жидкость возникает, а во втором случае она исчезает.
Абсолютная величина  характеризует мощность источника или стока.
характеризует мощность источника или стока.
Векторное поле, во всех точках которого дивергенция равна нулю, называют соленоидальным. Поток такого поля через любую замкнутую поверхность равен нулю.
Согласно формуле Остроградского-Гаусса поток и дивергенция векторного поля связаны между собой равенством
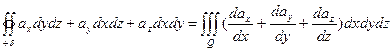 (3)
(3)
Которое имеет следующий смысл: поток векторного поля В через замкнутую поверхность  равен тройному интегралу по области, ограниченной этой поверхностью, от дивергенцией поля.
равен тройному интегралу по области, ограниченной этой поверхностью, от дивергенцией поля.
Решение. Применяя формулу (2):
1) 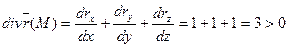
Физический смысл: каждая точка поля радиус-вектора 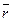 является источником постоянной мощности
является источником постоянной мощности
2) 
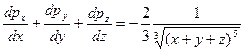
Физический смысл: точка поля М вектора 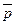 в зависимости от ее координат может быть или источником, или стоком. Например, точка
в зависимости от ее координат может быть или источником, или стоком. Например, точка 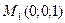 в которой
в которой
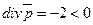
является стоком; точка 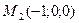 в которой
в которой
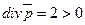
является источником.
3) 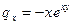
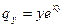
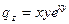
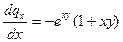 ;
; 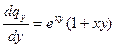 ;
; 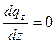
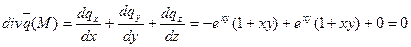
Физический смысл: В поле вектора 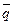 нет ни источников, ни стоков. Поток этого соленоидного поля через любую замкнутую поверхность равен нулю.
нет ни источников, ни стоков. Поток этого соленоидного поля через любую замкнутую поверхность равен нулю.
14. Используя формулу Остроградского-Гаусса решить задачу 12, т.е. найти поток векторного 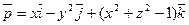 через поверхность эллипсоида
через поверхность эллипсоида 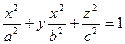 изнутри этой поверхности.
изнутри этой поверхности.
Решение. Найдем
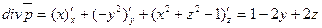 и подставляя в формулу (3) найдем
и подставляя в формулу (3) найдем
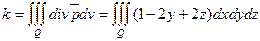
где Q– эллипсоид 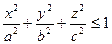
Полученный тройной интеграл расчленяем:
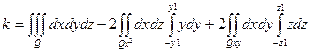
Где 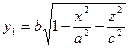 и
и 
Первый интеграл равен объему области Q, т.е. объему эллипсоида 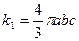
Второй и третий интегралы равны, т.к. равны нулю их внутренние простые интегралы от нечетной функции.
Следовательно, как и в решении задачи 12 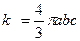 , Но решение значительно проще.
, Но решение значительно проще.
15. Найти дивергенцию векторного поля  в точке А(1;-1;3)
в точке А(1;-1;3)
Решение: 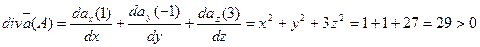
в точке А исток
16. Проверить, что векторное поле 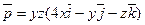 является соленоидным.
является соленоидным.
Решение:
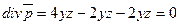
Во всех точках данного векторного поля 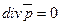 . Следовательно, векторное поле является соленоидальным. Поток такого поля через любую замкнутую поверхность равен нулю.
. Следовательно, векторное поле является соленоидальным. Поток такого поля через любую замкнутую поверхность равен нулю.
17. Вычислить циркуляцию поля вектора 1) 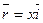 вдоль окружности
вдоль окружности 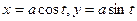 2)
2) 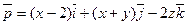 вдоль периметра треугольника с вершинами А(1;0;0) В(0;1;0) С(0;0;1); 3)
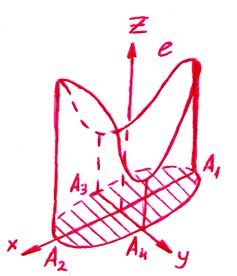
вдоль периметра треугольника с вершинами А(1;0;0) В(0;1;0) С(0;0;1); 3) 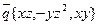 вдоль замкнутой линии (l):
вдоль замкнутой линии (l): 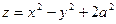 ,
, 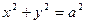 (см. рис) и вихревой вектор этого поля в точке А(
(см. рис) и вихревой вектор этого поля в точке А(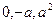 )
)
Линейным интегралом вектора 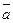 вдоль линии l называют криволинейный интеграл
вдоль линии l называют криволинейный интеграл 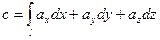 (1)
(1)
В силовом поле он выражает работу сил поля при перемещении точки вдоль линии l.
В случае замкнутой кривой этот интеграл называется циркуляцией поля вектора по контуру l.
Вихрем (или ротором) векторного поля, определяемого вектором 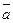 , называют вектор
, называют вектор
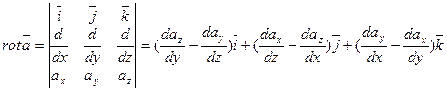 (2)
(2)
Доказать!
Если через точку М поля 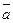 провести плоскость Р, определяемую единичным нормальным вектором
провести плоскость Р, определяемую единичным нормальным вектором 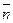 , то скалярное произведение
, то скалярное произведение 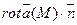 характеризует вращательную способность этого поля в точке М. Она зависит как от координат точки М, так и от направления плоскости Р и достигает наибольшей величины, равной
характеризует вращательную способность этого поля в точке М. Она зависит как от координат точки М, так и от направления плоскости Р и достигает наибольшей величины, равной 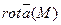 когда плоскость Р перпендикулярна
когда плоскость Р перпендикулярна 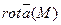 .
.
Векторное поле, во всех точках которого вихревой вектор равен нулю, называют потенциальным(или безвихревым). В потенциальном поле линейный интеграл, т.е. работа не зависит от формы линии, соединяющей какие-либо две его точки, а циркуляция всегда равна нулю.
Векторное поле, являющееся одновременно и соленоидальным и потенциальным, называют гармоническим.
Решение Применяя формулу (1), получим:
1) 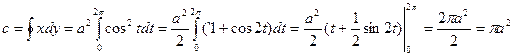
Если выбрать другое направление обхода данного контура, то результат будет иметь противоположный знак
2) 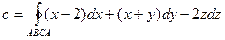
Периметр АВСА треугольника состоит из трёх отрезков, которые лежат на прямых, имеющих различные уравнения. Поэтому криволинейный интеграл по контуру АВСА вычисляем как сумму интегралов по отрезкам АВ, ВС и СА.
Составив уравнения прямой АВ: X+Y=1, Z=0 и исходя из этих уравнений преобразуем криволинейный интеграл по отрезку АВ в обыкновенный интеграл с переменной x.
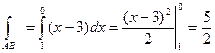
Для отрезка ВС: y+z=1; x=0;
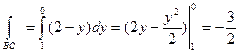
Для отрезка СА; x+z=1, y=o;
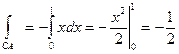
Следовательно 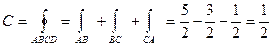
3) 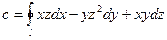
Для вычисления этого интеграла преобразуем данные уравнения кривой l в параметрические: полагая 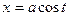 , получим из уравнения
, получим из уравнения 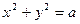 ,
, 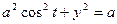 ,
, 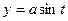
Соответственно из уравнения 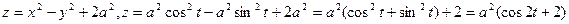
Пользуясь этими уравнениями, преобразуем криволинейный интеграл с в обыкновенный интеграл с переменной t, затем вычисляем его:
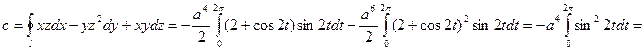
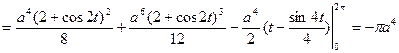
Вихревой вектор (rot) данного поля в любой точке М(x,y,z) находим по формуле (2)

В данной точке А(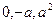 )
)
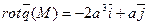
18. С какой наибольшей скоростью может возрастать функция  при переходе точки
при переходе точки 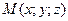 через точку
через точку 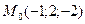 ? В каком направлении должна двигаться точка М при переходе через точку
? В каком направлении должна двигаться точка М при переходе через точку 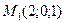 , чтобы функция убывала с наибольшей скоростью?
, чтобы функция убывала с наибольшей скоростью?
Наибольшая по величине скорость (возрастания или убывания) функции U(M) при переходе точки M через точку P численно равна модулю градиента функции в точке P. При этом функция будет возрастать или убывать с наибольшей скоростью, смотря по тому, будет ли точка M, переходя через точку P, двигаться по направлению градиента функции в точке P или по прямо противоположному направлению.
В соответствии с данными положениями, находим частные производные U и по формуле 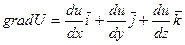 ее градиент в любой точке.
ее градиент в любой точке.
Градиентом функции (поля) U(M) называют вектор 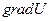 , который в каждой точке М совпадает с направлением нормали к поверхности (линии) уровня, проходящей через эту точку. Из всех производных функции U(M), взятых по различным направлениям, наибольшее значение всегда имеет производная по направлению градиента функции
, который в каждой точке М совпадает с направлением нормали к поверхности (линии) уровня, проходящей через эту точку. Из всех производных функции U(M), взятых по различным направлениям, наибольшее значение всегда имеет производная по направлению градиента функции
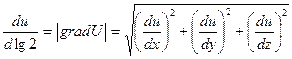
Градиент есть вектор скорости наибыстрейшего возрастания функции.
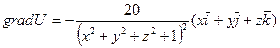
Далее находим: 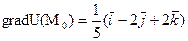 ; его модуль численно равный искомой наибольшей скорости возрастания функции U(M) при переходе M через
; его модуль численно равный искомой наибольшей скорости возрастания функции U(M) при переходе M через 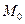 , будет:
, будет:
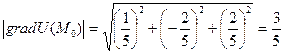
Далее: в каком направлении должна двигаться точка 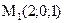 , чтобы функция U(M) убывала с наибольшей скоростью?
, чтобы функция U(M) убывала с наибольшей скоростью?
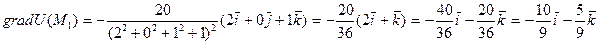
Чтобы функция U(M) убывала с наибольшей скоростью, при переходе через точку 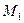 точка M должна двигаться в направлении вектора
точка M должна двигаться в направлении вектора
19. Найти производную функции 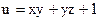 по направлению вектора
по направлению вектора 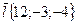 в любой точке и в точках
в любой точке и в точках 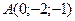 и
и 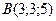 .
.
Найдем частные производные функции u и направляющие косинусы вектора 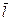 :
:
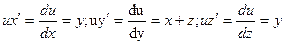 ;
;
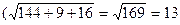
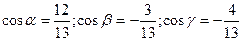
Подставляя в формулу:
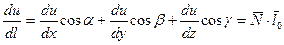
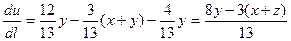
Подставляя координаты точек А и В получим:
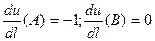
20.Найти точки, в которых функция 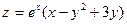 стационарна (т.е. точки, в которых производная по любому направлению равна нулю).
стационарна (т.е. точки, в которых производная по любому направлению равна нулю).
Чтобы в некоторой точке P производная функции по любому направлению была равна нулю, необходимо и достаточно, чтобы в этой точке все частные производные первого порядка функции одновременно обращались в нули. Согласно формуле:
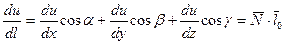 , где
, где 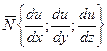 - нормальный вектор к поверхности уровня,
- нормальный вектор к поверхности уровня, 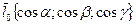 - единичный вектор направления
- единичный вектор направления  .
.
Поэтому, найдя частные производные:
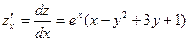 ,
, 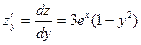 и решая систему уравнений:
и решая систему уравнений:
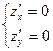 или
или 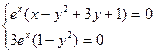 получим две точки: (-3;1) и (1;-1), функция
получим две точки: (-3;1) и (1;-1), функция 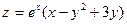 стационарна.
стационарна.
21. Найти вихревой вектор (rot) в любой точке векторного поля: 1) 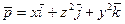 ; 2)
; 2) 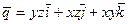 .
.
См. формулу 2 вопрос 17. Ответ: 1) 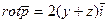 ; 2)
; 2) 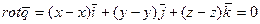 ;
; 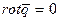 - потенциальное поле (безвихревое).
- потенциальное поле (безвихревое).
22. Проверить, что векторное поле вектора 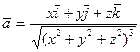 является гармоническим.
является гармоническим.
См. вопрос 17.
23. Найти линии уровня скалярного поля 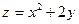 соответствующие значениям z=-2,-1,0,1,2. См. вопрос 8. Найти градиент этого поля в точках A(1;-1) и B(-2;-2).
соответствующие значениям z=-2,-1,0,1,2. См. вопрос 8. Найти градиент этого поля в точках A(1;-1) и B(-2;-2).
Ответ: 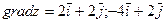
24. Теорема Умова-Пойнтинга.
Кроме уравнений Максвелла, большое значение в теории Электромагнитного поля имеет теорема Умова-Пойнтинга, которая описывает энергетические соотношения в поле.
Н.А. Умов с 1893 по 1911г. являлся профессором московского университета. В 1874г. защитил докторскую диссертацию «О движении Энергии в упругих средах», где рассмотрел вопрос о потоке энергии в упругих средах и о плотности потока энергии. Применительно к электромагнитному полю понятие о потоке энергии было развито Пойнтингом в 1885г.
Энергия электрического поля в единице объема равна 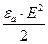 , соответственно энергия магнитного поля в единице объема
, соответственно энергия магнитного поля в единице объема 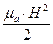 . Энергия в объеме
. Энергия в объеме 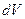 равна
равна 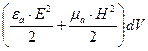 .
.
Можно показать, что 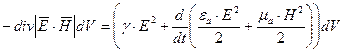 , где
, где 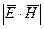 - векторное произведение
- векторное произведение 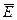 на
на 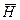 , для сокращения записи примем
, для сокращения записи примем 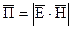 ;
; 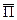 - это вектор, называемый вектором Пойнтинга; размерность его равна произведению размерностей E и H, т.е.
- это вектор, называемый вектором Пойнтинга; размерность его равна произведению размерностей E и H, т.е. 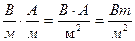 .
.
Таким образом, вектор Пойнтинга имеет размерность мощности, отнесенной к единице поверхности и направление его совпадает с направлением движения острия правого винта, если головку последнего вращать по кротчайшему направлению от 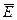 к
к 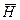 . Следовательно:
. Следовательно:
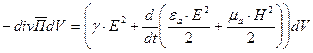 (1), где
(1), где 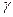 - удельная проводимость
- удельная проводимость  ;
; 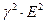 - энергия, выделяющаяся в виде теплоты в единице объема в единицу времени;
- энергия, выделяющаяся в виде теплоты в единице объема в единицу времени; 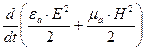 - скорость изменения запаса электромагнитной энергии в единице объема, в свою очередь скорость изменения электромагнитной энергии есть мощность.
- скорость изменения запаса электромагнитной энергии в единице объема, в свою очередь скорость изменения электромагнитной энергии есть мощность.
Рассмотрим (1) на некоторый объем конечных размеров. С этой целью проинтегрируем (1) по объему V:
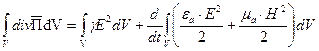 (2)
(2)
Можно показать, что:
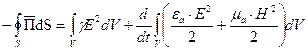 (3)
(3)
Формула (3) представляет собой теорему Умова-Пойнтинга для мгновенных значений. 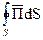 представляет собой поток вектора Пойнтинга сквозь любую замкнутую поверхность S, ограничивающую некоторый объем V.
представляет собой поток вектора Пойнтинга сквозь любую замкнутую поверхность S, ограничивающую некоторый объем V.
Т.к. 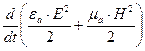 есть скорость изменения электромагнитной энергии, т.е. мощность, следовательно поток вектора Пойнтинга сквозь любую замкнутую поверхность, ограничивающую объем V, равен мощности, выделяющейся на приращение энергии электромагнитного поля.
есть скорость изменения электромагнитной энергии, т.е. мощность, следовательно поток вектора Пойнтинга сквозь любую замкнутую поверхность, ограничивающую объем V, равен мощности, выделяющейся на приращение энергии электромагнитного поля.
Теорему Умова-Пойнтинга следует трактовать как уравнение энергетического баланса.
Левая часть уравнения (3) есть мощность или энергия в единицу времени, доставляемая в виде потока вектора Пойнтинга внутрь некоторого объема; правая часть есть энергия, расходуемая в единицу времени внутри объема V.
Уравнение (3) было получено при условии, что среда внутри объема V однородна и изотропна- одинаковость (изотропия гр. tropos- поворот, направление) физ. свойств тела (среды) по всем направлениям. При обычных условиях газы, жидкости и аморфные тела изотропны, - а так же в предположении, что отсутствует отраженная волна и внутри объема нет источников электродвижущей силы. Если поле не изменяется во времени, то 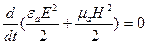 и
и 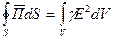
Следует также учесть, что уравнение (3) учитывает возможность прохождения потока вектора 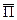 транзитом через объем V.
транзитом через объем V.
25. Показать справедливость утверждения, что электромагнитная энергия от места ее генерирования передается к месту ее потребления по диэлектрику (провода же в линиях передачи выполняют двоякую роль: они являются каналами, по которым проходит ток и организаторами структуры поля в диэлектрике).
Пусть энергия постоянного тока передается по коаксиальному кабелю (см. рисунок). Радиус жилы: 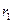 , внутренний радиус оболочки:
, внутренний радиус оболочки: 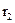 .
.
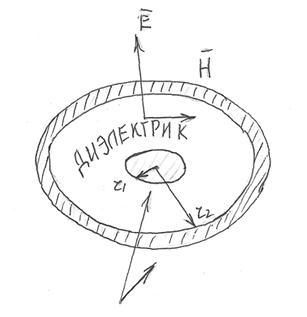
Примем проводимость материала жилы и оболочки настолько большой, что напряженности поля 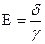 в жиле и оболочке стремятся к нулю. Пространство между жилой и оболочкой заполнено диэлектриком.
в жиле и оболочке стремятся к нулю. Пространство между жилой и оболочкой заполнено диэлектриком.
Убедимся, что энергия, передаваемая в единицу времени, равная 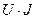 , действительно канализируется по диэлектрику.
, действительно канализируется по диэлектрику.
С этой целью подсчитаем поток вектора Пойнтинга через поперечное сечение диэлектрика, в рассматриваемом примере представляющее собой кольцо с внутренним радиусом 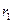 и наружным
и наружным 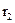 . Напряженность магнитного поля в диэлектрике по закону полного тока:
. Напряженность магнитного поля в диэлектрике по закону полного тока: 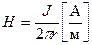 . Напряженность электрического поля в диэлектрике при постоянном токе определяется так же, как и в условиях электростатики:
. Напряженность электрического поля в диэлектрике при постоянном токе определяется так же, как и в условиях электростатики: 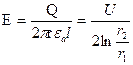 ,
,
где Q- полный заряд жилы на длине l; U- напряжение между жилой и оболочкой.
Следовательно, в некоторой точке диэлектрика, расположенной на расстоянии r от оси(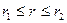 )
)
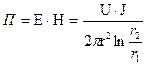 (
(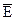 и
и 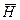 взаимно перпендикулярны).
взаимно перпендикулярны).
Поток вектора Пойнтинга через кольцо с радиусами 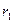 и
и 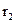 :
:
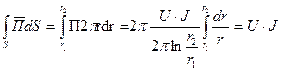
Таким образом, вся поступающая к приемнику энергия передается по диэлектрику. По жиле и оболочке энергия к приемнику не передается. Более того, если учесть, что 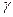 конечна и напряженность электрического поля в жиле и оболочке направлена по току и неравна нулю, то не трудно убедиться в наличии потока вектора Пойнтинга через боковую поверхность провода внутрь провода, т.е. провода сами потребляют энергию на покрытие тепловых потерь.
конечна и напряженность электрического поля в жиле и оболочке направлена по току и неравна нулю, то не трудно убедиться в наличии потока вектора Пойнтинга через боковую поверхность провода внутрь провода, т.е. провода сами потребляют энергию на покрытие тепловых потерь.
26. Определить 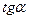 , составляемого напряженность электрического поля с нормалью к поверхности жилы в точке, принадлежащей поверхности жилы коаксиального кабеля, а также подсчитать величину поток вектора Пойнтинга через боковую поверхность жилы на длине в 1м. и сопоставить величину потока вектора Пойнтинга с потерями энергии в жиле на длине в 1м. Радиус медной жилы
, составляемого напряженность электрического поля с нормалью к поверхности жилы в точке, принадлежащей поверхности жилы коаксиального кабеля, а также подсчитать величину поток вектора Пойнтинга через боковую поверхность жилы на длине в 1м. и сопоставить величину потока вектора Пойнтинга с потерями энергии в жиле на длине в 1м. Радиус медной жилы 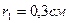 ; внутренний радиус оболочки
; внутренний радиус оболочки 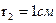 . Протекающий по кабелю постоянный ток J=50A. Напряжение между жилой и оболочкой U=10kB.
. Протекающий по кабелю постоянный ток J=50A. Напряжение между жилой и оболочкой U=10kB.
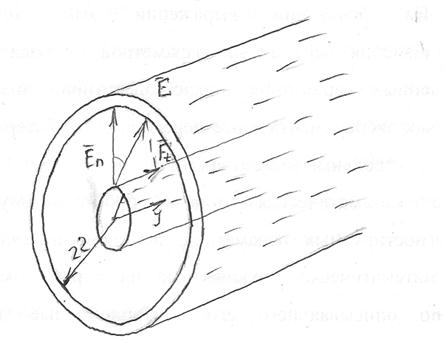
Нормальная составляющая напряженности электрического поля на поверхности жилы:
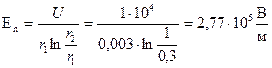
Тангенциальная составляющая напряженности электрического поля на поверхности жилы по закону Ома:
Вектор напряженности электрического поля 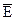 составляет с нормалью к поверхности жилы угол
составляет с нормалью к поверхности жилы угол 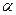 , тангенс которого:
, тангенс которого:
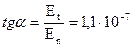
Напряженность магнитного поля на поверхности жилы по закону полного тока:

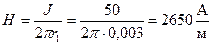
Для определения величины потока вектора Пойнтинга внутрь жилы на длине в 1м следует умножить составляющую вектора Пойнтинга 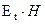 , проникающую внутрь жилы, на величину боковой поверхности жилы на длине в 1м, т.е.:
, проникающую внутрь жилы, на величину боковой поверхности жилы на длине в 1м, т.е.:
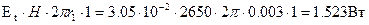
Эта величина равна потерям энергии в жиле кабеля на длине в 1м, т.е.:
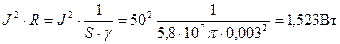
ч.т.д.
27. Теорема Умова-Пойнтинга в комплексной форме записи.
Перед тем как записать теорему Умова-Пойнтинга в комплексной форме, рассмотрим вопрос о полной мощности в цепи переменного тока. Полная мощность:
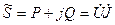
Пусть цепь переменного тока содержит последовательно соединенные активное сопротивление R, индуктивность L и емкость C.
Тогда реактивная мощность:
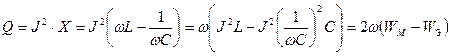
Здесь 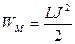 и
и 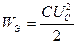 ,
,
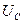 - напряжение на конденсаторе.
- напряжение на конденсаторе.
Таким образом, реактивная мощность равна разности между магнитной 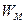 и электрической энергиями цепи, умноженной
и электрической энергиями цепи, умноженной 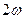 . Подобно тому как в цепи переменного тока для вычисления полной мощности
. Подобно тому как в цепи переменного тока для вычисления полной мощности 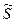 , надо умножить комплекс напряженности
, надо умножить комплекс напряженности 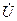 на сопряженный комплекс тока
на сопряженный комплекс тока 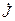 , вводится комплексный вектор Пойнтинга:
, вводится комплексный вектор Пойнтинга: 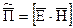
Вместо 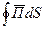 теперь будет:
теперь будет:
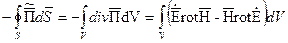
Так как 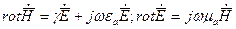 , следовательно,
, следовательно, 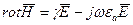 и
и 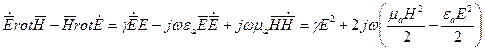 . Поэтому:
. Поэтому:
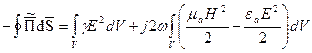 (1)
(1)
Первое слагаемое правой части уравнения (1) представляет собой активную мощность, второе – реактивную. Таким образом, теорему Умова-Пойнтинга можно записать еще в следующей форме:
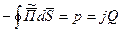
В таком виде ее часто используют для определения активного и внутреннего реактивного сопротивлений проводников на переменном токе.
28. Условия применимости уравнений Максвелла.
1. В уравнения Максвелла входят параметры 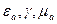 , которые характеризуют лишь усредненные в пространстве и времени величины, что вполне справедливо при низких частотах. Однако при низких частотах в диэлектриках существенную роль начинает играть диэлектрическая вязкость и другие явления. В ферромагнитных же веществах резко сказываются явления гистерезиса, магнитной вязкости и другие явления.
, которые характеризуют лишь усредненные в пространстве и времени величины, что вполне справедливо при низких частотах. Однако при низких частотах в диэлектриках существенную роль начинает играть диэлектрическая вязкость и другие явления. В ферромагнитных же веществах резко сказываются явления гистерезиса, магнитной вязкости и другие явления.
2. В первом уравнении Максвелла 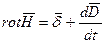 записаны две плотности тока- проводимости
записаны две плотности тока- проводимости 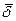 и электрического смещения
и электрического смещения 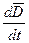 . Однако кроме этих токов существует третий вид тока – ток переноса (это собирательное название). под током переноса вообще понимают любой ток, природа которого отличается от тока проводимости и тока смещения, это, например, ток возникающий в электронной лампе вследствие термоэлектронной эмиссии.
. Однако кроме этих токов существует третий вид тока – ток переноса (это собирательное название). под током переноса вообще понимают любой ток, природа которого отличается от тока проводимости и тока смещения, это, например, ток возникающий в электронной лампе вследствие термоэлектронной эмиссии.
Ток переноса, также как и остальные виды токов, создают магнитное поле.
3. при чрезвычайно высоких частотах, когда длина волны становится соизмеримой с линейными размерами, характеризующими молекулярную структуру самого вещества, вещество нельзя рассматривать как континуум. В этом случае уравнения Максвелла должны быть заменены квантовой теорией поля.
29. Уравнения Максвелла для проводящей среды.
Рассмотрим особенности распространения электромагнитной волны в проводящей среде с проводимостью 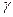 и магнитной проницаемостью
и магнитной проницаемостью 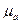 .
.
Обратимся к первому и второму уравнениям Максвелла, записанными в комплексной форме для синусоидально изменяющихся во времени E и H.
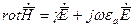 и
и 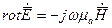
В проводящей среде даже при очень низких частотах произведение 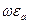 много меньше проводимости
много меньше проводимости 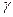 . поэтому с большой степенью точности слагаемым
. поэтому с большой степенью точности слагаемым 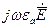 можно пренебречь в первом уравнении Максвелла.
можно пренебречь в первом уравнении Максвелла.
Таким образом, первое и второе уравнения Максвелла для проводящей среды приобретают вид:
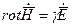 и
и 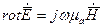
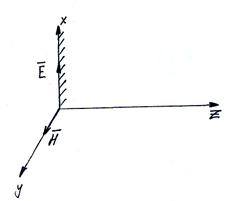
30. Плоская электромагнитная волна.
Под плоской электромагнитной волной понимают волну, векторы 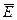 и
и 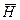 которой расположены в плоскости XOY, перпендикулярной направлению распространения волны (ось OZ) и измеряющуюся только в функции координаты Z и времени t.
которой расположены в плоскости XOY, перпендикулярной направлению распространения волны (ось OZ) и измеряющуюся только в функции координаты Z и времени t.
В дальнейшем под плоской волной будем понимать плоскую линейно поляризованную волну, в которой вектор 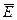 направлен вдоль одной оси, например, оси OX, а вектор
направлен вдоль одной оси, например, оси OX, а вектор 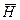 - вдоль другой, например, оси OY плоскости XOY.
- вдоль другой, например, оси OY плоскости XOY.
Изобразим графически положение плоской электромагнитной волны для одного и того же момента времени в двух плоскостях и в разных точках этих плоскостей.
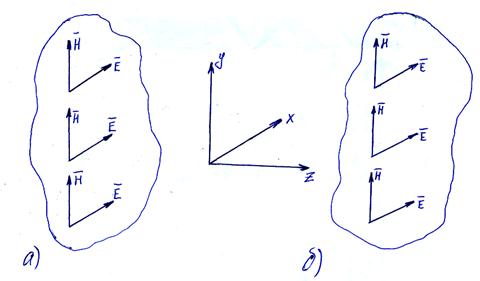
Во всех точках первой плоскости (а) напряженности H и E одинаковы по величине и направлению, также как и во второй плоскости (б), но напряженности в этих плоскостях не равны между собой. Т.к. в силу самого определения плоской электромагнитной волны 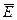 и
и 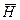 изменяются только по координате OZ, т.е. являются функциями только переменной Z и времени t.
изменяются только по координате OZ, т.е. являются функциями только переменной Z и времени t.
П.С. Как применить теорему Умова-Пойнтинга для определения комплексного сопротивления провода?
Определение активного и внутреннего индуктивного сопротивлений проводников на переменном токе.
Активное и внутреннее индуктивное сопротивления при переменном токе можно определить с помощью теоремы Умова-Пойнтинга в комплексной форме. С этой целью подсчитывают поток вектора Пойнтинга через боковую поверхность проводника на длине в 1м, делят его на квадрат тока, протекающего по проводнику, получают комплексное сопротивление проводника на единицу длины.
Действительно 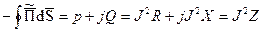 и
и 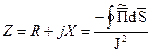 .
.
В качестве примера определим активное и внутренне индуктивное сопротивления цилиндрического провода на длине 1м.
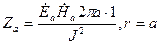
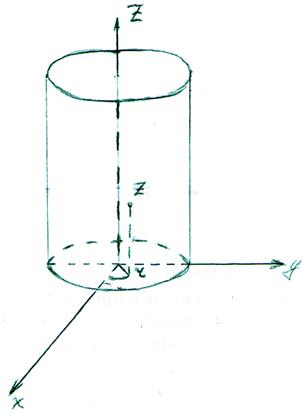
31. Экранирование в переменном электромагнитном поле.
Явление затухания электромагнитной волны в поверхностном слое металла используют для экранировки в переменном магнитном поле.
Электромагнитные экраны представляют собой полые цилиндрические, сферические или прямоугольные оболочки, внутрь которых помещают экранируемое устройство, например, катушку, индуктивность, измерительный прибор и т.п.
Экран выполняет две функции: 1)защищает устройство, заключенное в экран, от влияния внешнего по отношению к экрану электромагнитного поля; 2)защищает внешнее по отношению к экрану пространство от электромагнитного поля, создаваемого устройством, заключенном в экране.
Поскольку на расстоянии, равном длине волны, электромагнитная волна в металле почти полностью затухает, то для хорошей экранировки толщина стенки экрана примерно должна быть равна длине волны в металле. Практически приходиться учитывать и другие факторы (прочность экрана, стоимость и т.п.)
32. Принципы экранирования в электростатическом, магнитном и электромагнитных полях.
Электростатическое экранирование основано на компенсации внешнего поля полем зарядов, появившихся на стенках экрана из проводящего материала вследствие электростатической индукции. Толщина стенок экрана при электростатическом экранировании в отличии от экранирования в магнитном и электромагнитном полях может быть сколь угодно малой.
Экранирование в магнитном поле постоянного тока основано прежде всего на том, что силовые линии магнитного поля преимущественно проходят по участкам с меньшим магнитным сопротивлением (по стенкам экрана).
Экранирование в переменном электромагнитном поле основано, главным образом, на том, что электромагнитная волна, проникающая в стенки экрана, быстро затухает, расходуя энергию на покрытие потерь, обусловленных вихревыми токами в стенках экрана.
Если экран выполнен из ферромагнитного материала и частота  относительно низкая, то экранирование достигается не только за счет затухания волны, но и за счет стремления силовых линий магнитного поля пройти по участкам с меньшим магнитным сопротивлением.
относительно низкая, то экранирование достигается не только за счет затухания волны, но и за счет стремления силовых линий магнитного поля пройти по участкам с меньшим магнитным сопротивлением.
33. Нагрев металлических деталей и несовершенных диэлектриков в электромагнитном поле.
Нагрев металлических деталей перед ковкой и штамповкой, сушку древесины, наплавку и реставрацию инструментов можно производить при помещении этих предметов (деталей) в электромагнитное поле невысокой частоты (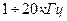 ).
).
Стальные изделия, например валы, шестеренки, иногда подвергают поверхностной закалке, помещая их в электромагнитное поле более высокой частоты (порядка 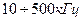 ).
).
Эффект поверхностной закалки возникает вследствие энергии, выделяющейся в виде тепла в проводящем теле, которая равна:
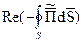
Электромагнитная волна, проникая в толщу металла, быстро затухает. Поэтому теплота выделяется практически лишь в относительно поверхностном слое стального изделия.
Под действием теплоты, выделившейся в поверхностном слое, последний быстро разогревается до температуры, необходимой для поверхностной закалки.
Высокочастотные используют также для нагрева несовершенных диэлектриков, проводимость которых, хотя и мала, но не равна нулю. Так, область еще более высоких частот (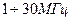 ) используется для высокочастотного нагрева пластмасс перед штамповкой, для термической обработки пищевых продуктов, вулканизации резины и многих других целей.
) используется для высокочастотного нагрева пластмасс перед штамповкой, для термической обработки пищевых продуктов, вулканизации резины и многих других целей.
34. Распространение плоской электромагнитной волны в однородном проводящем пространстве.
Электромагнитная волна проникает из диэлектрика в проводящую среду и распространяется в ней. Будем считать, что проводящая среда простирается теоретически в бесконечности, то падающая волна в толще проводящей среды не встречает границы, которая препятствовала ее распространению, то отраженной волны в данном случае не возникает.
Можно показать, что мгновенные значения H и E изменяются в соответствии с формулами:
 ,
,
где 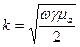 ,
,  - фазовый сдвиг, определяемый из начальных условий.
- фазовый сдвиг, определяемый из начальных условий.
Амплитуды 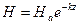 и
и 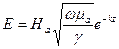 с увеличением Z уменьшаются по показательному закону.
с увеличением Z уменьшаются по показательному закону.
Изобразим качественно правильно графики H в функции Z. Если принять 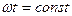 , то на графике мгновенных значений H в функции Z при
, то на графике мгновенных значений H в функции Z при 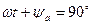 будет получена кривая (1) и при
будет получена кривая (1) и при 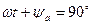 кривая (2).
кривая (2).
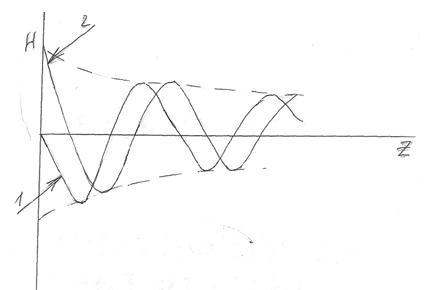
Для того чтобы охарактеризовать насколько быстро уменьшается амплитуда падающей волны по мере проникновения волны в проводящую среду, вводят понятие «глубина проникновения».
35. Глубина проникновения и длина волны.
Под глубиной проникновения 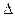 понимают расстояние вдоль направления распространения волны (в нашем случае вдоль оси Z), на котором амплитуда падающей волны H (или E) уменьшается в е=2,71 раз. Глубину проникновения определяют с помощью выражения:
понимают расстояние вдоль направления распространения волны (в нашем случае вдоль оси Z), на котором амплитуда падающей волны H (или E) уменьшается в е=2,71 раз. Глубину проникновения определяют с помощью выражения:
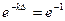 , откуда
, откуда 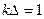 или
или 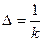
Глубина проникновения 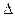 зависит от свойств проводящей среды (
зависит от свойств проводящей среды (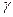 и
и 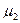 ) и частоты
) и частоты  . Так если электромагнитная волна имеет частоту f=5000Гц и проникает в проводящую среду, у которой
. Так если электромагнитная волна имеет частоту f=5000Гц и проникает в проводящую среду, у которой 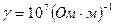 и
и 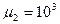 , то
, то
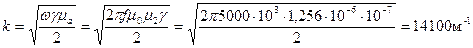
Тогда глубина проникновения 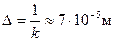 , т.е. на расстоянии в 0,007см=0,07мм амплитуды H и E уменьшились в 2,71 раза.
, т.е. на расстоянии в 0,007см=0,07мм амплитуды H и E уменьшились в 2,71 раза.
Под длиной волны 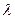 в проводящей среде понимают расстояние вдоль распространения волны (вдоль оси OZ), на котором фаза колебаний изменяется на
в проводящей среде понимают расстояние вдоль распространения волны (вдоль оси OZ), на котором фаза колебаний изменяется на 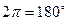 .
.
Длину волны определяют из выражения:
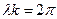 , отсюда
, отсюда 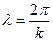
Для нашего примера: 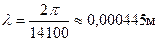
Иногда пользуются понятием фазовой скорости распространения электромагнитной волны в проводящей среде. Под фазовой скоростью понимают скорость, с которой надо было бы перемещаться вдоль оси t, чтобы колебание имело одну и ты же фазу.
Фаза определяется выражением: 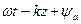 . Так как производная от постоянной величины
. Так как производная от постоянной величины 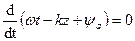 , или
, или 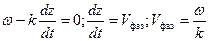 .
.
Для нашего примера: 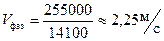 .
.
Задачи.
36. Вывести из уравнений Максвелла волновые уравнения для однородной непроводящей среды, считая плотность объемных зарядов р = 0. Параметры среды: 
Решение. Уравнения Максвелла в рассматриваемом случае можно записать следующим образом:
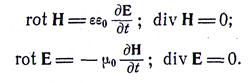
Возьмем ротор от ротора напряженности электрического поля:
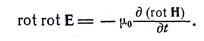
Подставив значение rot H и раскрыв выражение «ротор от ротора»; (формула 1.22), получим
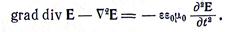
Так как divE = 0, то
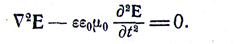
Полученное уравнение называется волновым. Аналогично получим
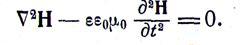
Величину  можно обозначить через
можно обозначить через 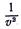 . Следовательно, величина
. Следовательно, величина
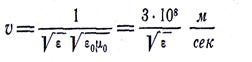
представляет собой скорость распространения электромагнитной волны в данной неограниченной среде.
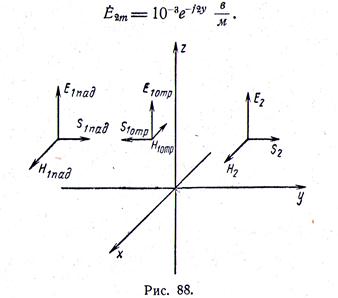
37. Плоская гармоническая электромагнитная волна распространяется по направлению оси у и при у = 0 переходит из одного диэлектрика в другой. Ось z параллельна направлению вектора Е (рис. 88). Параметры сред следующие:
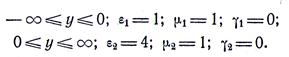
Угловая частота 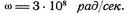 Амплитуда вектора напряженности электрического поля при у = 0 равна Еm=1 мВ/м.
Амплитуда вектора напряженности электрического поля при у = 0 равна Еm=1 мВ/м.
Требуется найти величину векторов напряженности электрического и магнитного полей.
Решение. В области  не будет отраженных волн,
не будет отраженных волн,
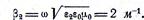 так как она неограниченна в направлении распространения. Комплексная амплитуда напряженности электрического поля в этой области
так как она неограниченна в направлении распространения. Комплексная амплитуда напряженности электрического поля в этой области 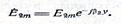
Коэффициент фазы
По условию 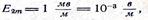 поэтому
поэтому
Мгновенное значение вектора напряженности электрического поля 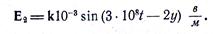
Волновое сопротивление в среде с 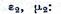
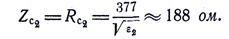
Следовательно, вектор напряженности магнитного поля

В области 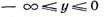 имеют место и падающие, и отраженные от поверхности раздела двух сред волны, поэтому комплексные амплитуды векторов напряженности электрического и магнитного полей будут следующие:
имеют место и падающие, и отраженные от поверхности раздела двух сред волны, поэтому комплексные амплитуды векторов напряженности электрического и магнитного полей будут следующие:
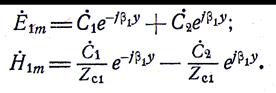
Для определения постоянных интегрирования 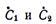 надо использовать граничные условия: при y = 0
надо использовать граничные условия: при y = 0
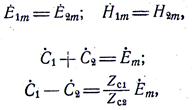
или
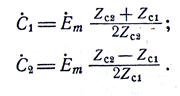
откуда
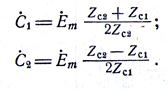
Волновое сопротивление в среде с 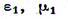
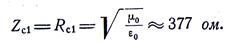
Следовательно, коэффициент прохождения
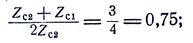
коэффициент отражения

Коэффициент фазы
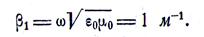
Комплексные амплитуды напряженностей электрического и магнитного полей равны
а соответствующие векторы в мгновенных значениях будут 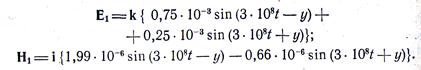
38. Подсчитать поток вектора Пойнтинга сквозь сферическую поверхность радиусом  Найти сопротивление излучения.
Найти сопротивление излучения.
Решение. Центр сферической поверхности с радиусом г поместим в начале координат (рис. 92). Поток вектора Пойнтинга сквозь эту поверхность равен 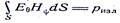 и представляет
и представляет
собой мгновенную мощность излучения.
Разобьем сферическую поверхность на элементарные кольцевые площадки:
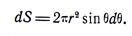
Тогда искомый поток будет равен
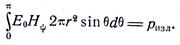
Подставив выражения проекций 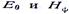 , найденные в задаче 5.17, получим
, найденные в задаче 5.17, получим
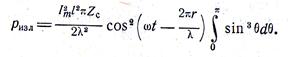
Так как 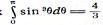 , то
, то
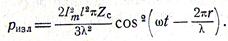
Средняя мощность излучения за период Т
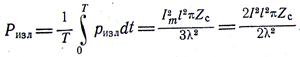
Так как волновое сопротивление воздуха
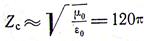 ,
,
то средняя мощность излучения
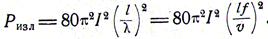
Сопротивление излучения
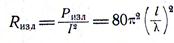
Рациональное и эффективное использование имеющихся природных ресурсов является одним из наиболее актуальных вопросов развития современного общества, так как большинство ресурсов, необходимых для жизнедеятельности общества и человека, относятся к невосполнимым или частично восполнимым. В этих условиях рациональное, экономичное использование ресурсов всех видов является важ
|
Дата добавления: 2014-01-07; Просмотров: 659; Нарушение авторских прав?; Мы поможем в написании вашей работы!