
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Второе уравнение Максвелла
|
|
|
|
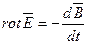 (6.1) Физический смысл этого уравнения состоит в том, что всякое изменение магнитного поля во времени (
(6.1) Физический смысл этого уравнения состоит в том, что всякое изменение магнитного поля во времени ( ) в какой либо точке поля возбуждает вихрь или ротор электрического поля (
) в какой либо точке поля возбуждает вихрь или ротор электрического поля (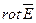 ) в той же точке поля, т.е. вызывает вихревое электрическое поле.
) в той же точке поля, т.е. вызывает вихревое электрическое поле.
Второе уравнение Максвелла представляет собой дифференциальную форму закона электрической индукции.
Чтобы убедиться в этом, мысленно возьмем некоторый замкнуты контур, расположенный в переменном электрическом поле. Переменный магнитный поток, пронизывающий контур, наведет в нем ЭДС.
 , где Ф - магнитный поток (поток магнитной индукции). Если магнитное поле однородное, то Ф через плоскую поверхность с площадью S, равен
, где Ф - магнитный поток (поток магнитной индукции). Если магнитное поле однородное, то Ф через плоскую поверхность с площадью S, равен  ,
,
но  , поэтому
, поэтому  , причем площадка
, причем площадка 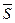 опирается на контур
опирается на контур 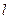 .
.
На основании теории Стокса  , поэтому
, поэтому 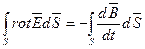 .
.
Это равенство должно выполняться при любых площадях S, то возможно только в том случае, когда равны подынтегральные функции обоих интегралов, следовательно 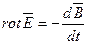 .
.
Знак «минус» в данной форме, как и в формуле  , объясняется тем, что в основу положено правило правого винта (правилом буравчика). Если завинчивать правый винт так, что положительное направление вектора магнитной индукции
, объясняется тем, что в основу положено правило правого винта (правилом буравчика). Если завинчивать правый винт так, что положительное направление вектора магнитной индукции  в некоторой точке пространства при возрастании индукции в этой точке совпадает с направлением острия винта, то положительное направление для вектора напряженности электрического поля
в некоторой точке пространства при возрастании индукции в этой точке совпадает с направлением острия винта, то положительное направление для вектора напряженности электрического поля 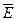 при составлении циркуляции вектора
при составлении циркуляции вектора 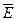 бесконечно малого контура, окружающего эту точку и лежащего в плоскости, перпендикулярно вектору
бесконечно малого контура, окружающего эту точку и лежащего в плоскости, перпендикулярно вектору  , совпадает с направлением вращения головки винта. Знак «минус» в правой части уравнения (6.1) поставлен для того, чтобы привести в соответствие действительное направление для
, совпадает с направлением вращения головки винта. Знак «минус» в правой части уравнения (6.1) поставлен для того, чтобы привести в соответствие действительное направление для 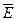 при оговоренных ранее условиях с направлением, принятым для
при оговоренных ранее условиях с направлением, принятым для 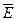 за положительное.
за положительное.
Как в первом, так и во втором уравнение Максвелла участвуют частные (не полные)
производные во времени. Это объясняется тем, что уравнения Максвелла записаны для таких тел и контуров, которые неподвижны к выбранной системе координат.
В переменном электромагнитном поле кроме силовых линий электрического поля, «начинающихся» и «оканчивающихся» на электрических зарядах (как в электростатическом поле) могу быть и замкнутые на себе силовые линии электростатического поля, охватывающие замкнутые на себя силовые линии магнитного поля.
7 .Уравнение Максвелла в комплексной форме записи.
Уравнение 2.1 и 6.1 записаны для мгновенных значений Н и Е. Если Н и Е изменяются во времени синусоидально, то можно воспользоваться символическим методом и записать эти уравнения в комплексной форме. Т.к. 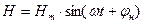 и
и 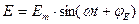 , в соответствии с формулой Эйлером:
, в соответствии с формулой Эйлером: 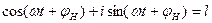
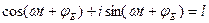
можно записать  , где
, где 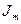 - мнимая часть или условно,
- мнимая часть или условно, 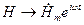 , где комплексная амплитуда
, где комплексная амплитуда  . Аналогично
. Аналогично 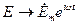 (
(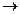 значок соответствия).
значок соответствия).
Т.к. напряженности Е и Н, кроме того, что они меняются во времени по синусоидальному закону являются функциями векторными, т.е. определенным образом ориентированными в пространстве векторам, то над ними ставят черточку и точку: 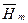 и
и 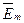 .
.
Черточка означает, что речь идет о векторе в пространстве, точка - о том, что проекция этого вектора на любую из координатных осей, во времени изменяется синусоидально.
Тогда 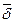 можно заменить на
можно заменить на  , где
, где 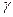 - удельная проводимость, характеризующая свойство среды проводить ток,
- удельная проводимость, характеризующая свойство среды проводить ток, 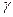 зависит от физических свойств проводящего материала и температуры. Измеряется в
зависит от физических свойств проводящего материала и температуры. Измеряется в 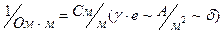
Так как  (
(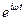 как постоянную величину можно вынести за знак ротора). После преобразования первое уравнение Максвелла в комплексной форме будет иметь вид:
как постоянную величину можно вынести за знак ротора). После преобразования первое уравнение Максвелла в комплексной форме будет иметь вид: 
Соответственно второе уравнение Максвелла в комплексной форме будет иметь вид: 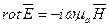
8.Построить линии уровня плоских скалярных полей: 1)  2)
2)  3)
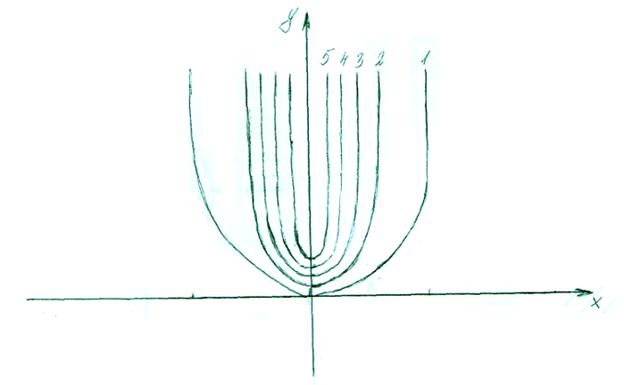
3)  , соответствующее значениям u=1,2,3,4,5.
, соответствующее значениям u=1,2,3,4,5.
Скалярным полем называется плоская или пространственная область с каждой точкой М с которой связанно определенное значение некоторой скалярной физической величины U=U(М).
Задание скалярной величины и равносильно заданию скалярной (числовой) функции U(M).Функция U(M), определяющая плоское скалярное поле, как функция точки М(х,у), зависит от двух переменных U=u(х,у).
Линией уровня плоского скалярного поля называют совокупность точек плоскости, в которых функция этого поля имеет одинаковые значения.
Линия уровня, во всех точках которых функция поля U(х,у) имеет одно и тоже значении С, определяется уравнением U(х,у)=С; различным постоянным значениям 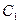 ,
, ,
, …функции поля соответствуют различные линии уровня: U(х,у) =
…функции поля соответствуют различные линии уровня: U(х,у) =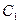 , U(х,у) =
, U(х,у) = , U(х,у) =
, U(х,у) =
Решение:
1)Пологая U=1,2,3,4,5,получим уравнения соответствующих линий уровня: х+у=1, х+у=2,
х+у=3, х+у=4, х+у=5. Построив эти линии в прямоугольной системе координат ХОУ, получим прямые параллельные биссектрисе 2-го и 4-го координатных углов, которые и являются геометрической интерпретацией линий уровня скалярного поля.

2)Написав уравнения линий уровня: 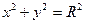 ; (
; (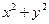 =1;
=1;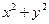 =2;
=2;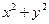 =3;
=3;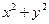 =4;
=4; 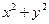 =5) построив их в плоскости ХОУ получим окружности с радиусом R с центром в начале координат(R=1;1,4;1,7;2;2,2)
=5) построив их в плоскости ХОУ получим окружности с радиусом R с центром в начале координат(R=1;1,4;1,7;2;2,2)

3) Линии уровня: 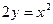 ,
,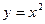 ,
, ,
, ,
,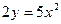 представляют собой параболы симметричные оси ОУ с общей вершиной в начале координат.
представляют собой параболы симметричные оси ОУ с общей вершиной в начале координат.
9.Найти производную функцию 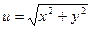 в точке М(3,4):
в точке М(3,4):
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2014; Нарушение авторских прав?; Мы поможем в написании вашей работы!