По характеру спотворення проекцій поділяють на

1. рівнокутні,

2. рівновеликі,

3. довільні.

Рівнокутні проекції – це такі, де зберігається подібність фігур земного еліпсоїда і на проекції. Рівновеликі проекції зберігають площі без спотворень. Такі проекції зручні для виміру площ об'єктів. Проте в них особливо значно порушені кути і форми, що особливо помітно для великих територій. Наприклад, на карті світу (мал.) приполярні області виглядають сильно сплюснутими.

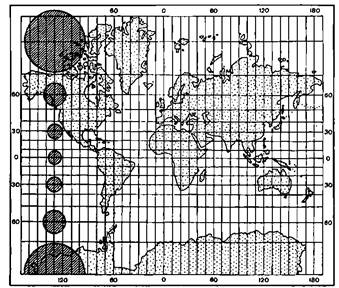
Рівновеликі проекції забезпечують зображення розміру площ сфери без спотворення на площині. Рівнокутні проекції - залишають без спотворень кути і форми контурів, показаних на карті (раніше такі проекції називали конформними). Елементарне коло в таких проекціях завжди залишається колом, але розміри її сильно міняються (мал.).

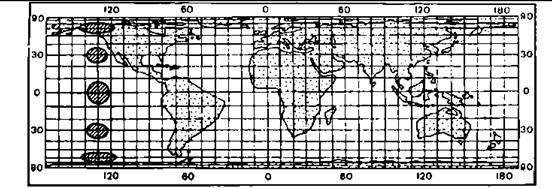
Такі проекції особливо зручні для визначення напрямів і прокладення маршрутів по заданому азимуту, тому їх завжди використовують на навігаційних картах. Зате карти, залишені в рівнокутних проекціях, мають значні спотворення площ.

Довільні (рівнопроміжні) проекції – це такі проекції, в яких масштаб довжин по одному з головних напрямів постійний і зазвичай дорівнює головному масштабу карти. Відповідно розрізняють проекції рівнопроміжні по меридіанах – в них без спотворень залишається масштаб уздовж меридіанів, і рівнопроміжні по паралелях - в них зберігається постійним масштаб уздовж паралелі. У таких проекціях присутні спотворення площ і кутів, але вони як би урівноважуються.

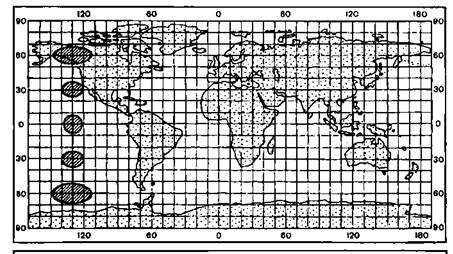
Довільні проекції - це усе інші види проекцій, в яких в тих або інших довільних співвідношеннях спотворюються і площі, і кути.

За способом побудови проекції поділяються на:

· циліндричні,

· конічні,

· багатогранні,

· перспективні.

У циліндричних проекціях проектування з кулі (еліпсоїда) ведеться на поверхню дотичного або січного циліндра, а потім його бічна поверхня розгортається в площину.

Якщо вісь циліндра співпадає з віссю обертання Землі, а поверхня торкається кулі по екватору (чи січе його по паралелях), то проекція називається нормальною (прямою) циліндричною. Тоді меридіани нормальної сітки з'являються у вигляді рівновіддалених паралельних прямих, а паралелі - теж у вигляді прямих, перпендикулярних до них. У таких проекціях менше всього спотворень в тропічних і приекваторіальних областях.

Якщо вісь циліндра розташована в площині екватора, то це - поперечна циліндрична проекція. Циліндр торкається кулі по меридіану, спотворення уздовж нього відсутні, і отже у такій проекції найвигідніше зображувати території, витягнуті з півночі на південь. У тих випадках, коли вісь допоміжного циліндра розташована під кутом до площини екватора, проекція називається косою циліндричної. Вона зручна для витягнутих територій, орієнтованих на північний захід або північний схід.

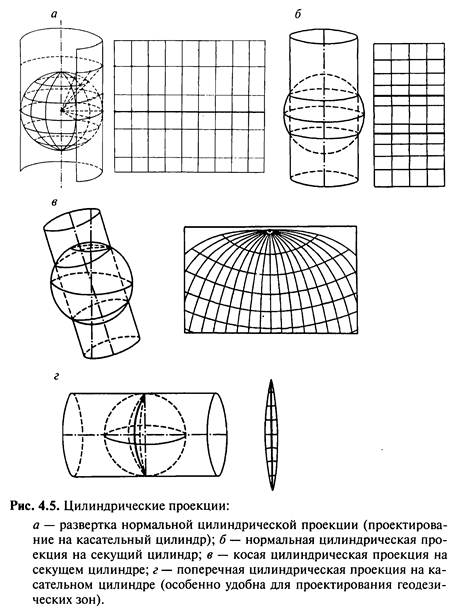
У конічних проекціях поверхня кулі (еліпсоїда) проектується на поверхню дотичного або січного конуса, після чого вона як би розрізається по лінії і розгортається в площину. Точно так, як і у попередньому випадку, розрізняють нормальну (пряму) конічну проекцію, коли вісь конуса співпадає з віссю обертання Землі, поперечну конічну - вісь конуса лежить в площині екватора і косу конічну - якщо вісь конуса нахилена до площини екватора.

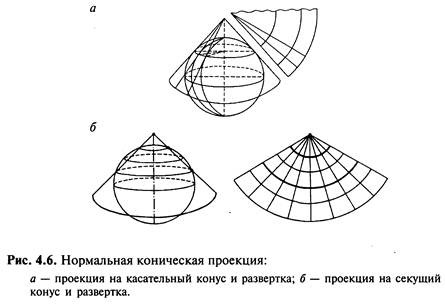
У нормальній конічній проекції меридіани представляють собою прямі, що розходяться з точки полюса, а паралелі – дуги концентричних кіл. Уявний конус торкається Земної кулі або січе його в районі середніх широт, тому в такій проекції найзручніше картографувати витягнуті із заходу на схід в середніх широтах території Росії, Канади, США.

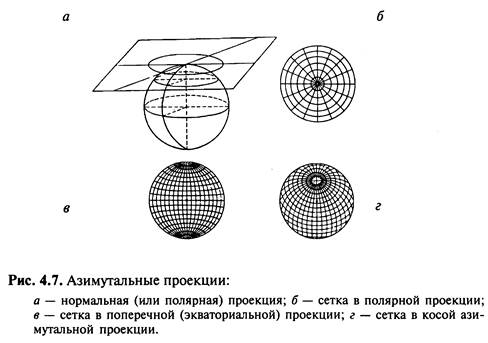
Азимутальні проекції - поверхня Земної кулі (еліпсоїда) переноситься на дотичну або січну площину. Якщо площина перпендикулярна до осі обертання Землі, то виходить нормальна (полярна) азимутна проекція. Паралелі у ній є концентричними колами, а меридіани - радіусами цих кіл. У цій проекції завжди картографують полярні області нашій і інших планет. Якщо площина проекції перпендикулярна до площини екватора, то виходить поперечна (екваторіальна) азимутальна проекція. Вона завжди використовується для карт півкуль. А якщо проектування виконане на дотичну або січну допоміжну площину, що знаходиться під будь-яким кутом до площини екватора, то виходить коса азимутальна проекція.

Можна показати, що азимутальні проекції є граничним випадком конічних, коли кут при вершині конуса як би стає рівним 180°.

У перспективних проекціях точки сфери проектуються на площину по прямих лініях. Якщо площина дотична до екватора, розташована паралельно обертання Землі, проекція називається - екваторіальною. Коли площина розташована паралельно горизонту, то проекція називається горизонтальною.

Умовні проекції - проекції, для яких не можна підібрати простих геометричних аналогів. Їх будують, виходячи з яких-небудь заданих умов, наприклад бажаного виду географічної сітки, того або іншого розподілу спотворень на карті, заданого виду сітки та ін. (мал. 4.9) Зокрема, до умовних належать псевдоциліндричні, псевдоконічні, псевдоазимутальні і інші проекції, отримані шляхом перетворення одній або декількох початкових проекцій.

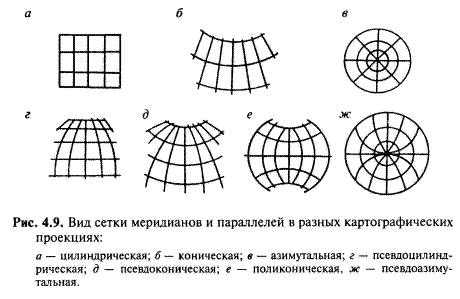
Псевдоциліндричні проекції - проекції, в яких паралелі - прямі (як і в нормальних циліндричних проекціях) середній меридіан - перпендикулярна їм пряма, а інші меридіани - криві, що збільшують кривизну у міру видалення від середнього меридіана. Найчастіше ці проекції застосовують для карт світу і Тихого океану.

Псевдоконічні проекції - такі, в яких усі паралелі зображуються дугами концентричних кіл (як в нормальних конічних), середній меридіан - пряма лінія, а інші меридіани - криві, причому кривизна їх зростає з видаленням від середнього меридіана. Застосовуються для карт Росії, Євразії

інших материків.

Поліконічні проекції - проекції, що отримуються як би в результаті проектування кулі (еліпсоїда) на безліч конусів. У нормальних поліконічних проекціях паралелі представлені дугами ексцентричних кіл, а меридіани -криві, симетричні відносно прямого середнього меридіана. Найчастіше ці проекції застосовуються для карт світу.

Псевдоазимутальні проекції - видозмінені азимутальні проекції. У полярних псевдоазимутальних проекціях паралелі представляють собою концентричні кола, а меридіани – криві лінії, симетричні відносно одного або двох прямих меридіанів. Поперечні і косі псевдоазимутальні проекції мають загальну овальну форму і зазвичай застосовуються для карт Атлантичного океану або Атлантичного океану разом з Північним Льодовитим.

Багатогранні проекції - проекції, що отримуються шляхом проектування на поверхню многогранника дотичного чи січного кулі (еліпсоїда). Найчастіше кожна грань представляє собою рівнобічну трапецію, хоча можливі і інші варіанти (наприклад, шестикутники, квадрати, ромби). Різновидом багатогранних є багатосмугові проекції, причому смуги можуть "нарізатися" і по меридіанах, і по паралелях. Такі проекції вигідні тим, що спотворення в межах кожної грані або смуги зовсім невеликі, тому їх завжди використовують для багатолистих карт. Топографічні і оглядово-топографічні створюють виключно в багатогранній проекції, і рамка кожного листа є трапецією, складеною лініями меридіанів і паралелей. За це доводиться розплачуватися - блок листів карт не можна поєднати по загальних рамках без розривів.

3. Для складання топографічних карт у країнах СНД з 1928 р. прийнята поперечно-циліндрична рівнокутна проекція К.Ф. Гаусса. Застосовуючи проекцію Гаусса, усю земну поверхню поділяють меридіанами на шести - або триградусні зони. Кожна зона проектується на поверхню свого циліндра, дотичного до земної кулі по середньому (осьовому) меридіану зони (рис. 2.4).

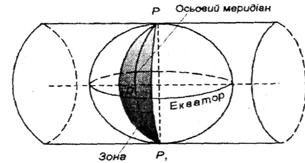
Рис. 2.4. Проекція Гаусса

Розподіл земної поверхні на зони при зображенні її на площині в проекції Гаусса викликано тим, що при великому віддаленні точки від осьового меридіана відбуваються дуже великі спотворення в цій точці на карті. Вибір зони шириною в 3º або 6° залежить від масштабу карти, що складається. При складанні карти масштабу 1:10 000 або дрібніше застосовують шестиградусну зону, а при складанні карти масштабу 1:5000 або крупніше - триградусну.

Шестиградусні зони нумеруються арабськими цифрами, починаючи від Грінвичського меридіана, із заходу на схід. Порядковий номер зони N зв'язаний з номером колони п аркуша співвідношенням:

N = п-30

Довготи осьових меридіанів шестиградусних зон L₀ знаходять за формулою

L₀ = 6°N - 3°

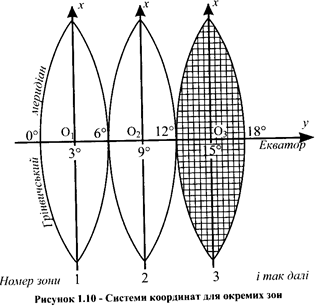
Осьовий меридіан зони та екватор зображують перпендикулярними одна до одної лініями, всі інші меридіани – кривими, що сходяться у полюсах, а паралелі -кривими, повернутими своїми випуклостями до екватора. Лінії на осьовому меридіані відображаються у масштабі карти без спотворень. Масштаб зображень об'єктів в інших частинах зони можна визначити за формулою

М=1+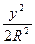

де у - відстань від осьового меридіана, а R - радіус Землі.

У кожній зоні застосовують свою систему прямокутних координат: за вісь ординат приймають екватор, а за вісь абсцис – осьовий меридіан.

Положення точки на фізичній поверхні Землі характеризується системою координат.

Координати – це кутові чи лінійні величини, що визначають положення точки на площині, в просторі чи на будь-якій іншій поверхні, в тому числі і на еліпсоїді, відносно прийнятого початку їх відліку.

Лінії та площини, відносно яких визначають положення точок, називаються відповідно осями координат та координатними площинами.

Основними системами координат у геодезії служать географічна (геодезична та астрономічна) та прямокутна. Поряд з тим застосовують такі системи як полярна, біполярна, місцеві системи прямокутних координат та інші.

Географічними координатами називаються широта та довгота точки, що визначаються напрямками нормалі до поверхні кулі, еліпсоїда, геоїда.

У геодезичній системі координат положення точки характеризується геодезичною широтою (В), геодезичною довготою (L) та геодезичною висотою (Н). Координатними площинами, відносно яких визначають положення точок, є площина екватора земного еліпсоїда та площина початкового меридіана. Геодезичні координати дають можливість обробляти результати геодезичних вимірів в єдиній для всієї поверхні Землі системі координат.

Геодезичною широтою називають кут, утворений нормаллю до поверхні земного еліпсоїда в даній точці та площиною його екватора. Широти можуть бути північні та бути зі знаком плюс, якщо відраховуються від екватора на північ, або південні, якщо відраховуються від екватора на південь і бути зі знаком мінус. За абсолютною величиною вони можуть бути від 0° до 90°.

Геодезичною довготою називають двогранний кут між площиною геодезичного меридіана даної точки М та початкового геодезичного меридіана. Довготи відраховуються від початкового меридіана (Грінвичського) в напрямку із заходу на схід від 0° до 360° або в обидві сторони від 0° до 180° з вказівкою відповідного слова "східна" або "західна".

Геодезичною висотою точки М, розташованої на фізичній поверхні Землі, називають відстань по нормалі від цієї точки до її проекції на поверхні земного еліпсоїда.

Геодезичні координати можуть бути поширені на всю поверхню земного еліпсоїда, і в цьому їх переваги. Однак важко застосовувати їх при значних геодезичних роботах, оскільки пов'язано це з громіздкими обчисленнями навіть при невеликих відстанях. Тому ці координати мають широке застосування лише при дрібномасштабному картографуванні.

Широкого поширення в практиці геодезичних робіт набула поперечно-циліндрична проекція Гаусса. У цій проекції найбільш зручнішою у застосуванні прийнято вважати прямокутну систему координат (рис. 2.7), причому в кожній зоні береться своя система координат: за вісь абсцис приймається осьовий меридіан, а за вісь ординат - екватор.

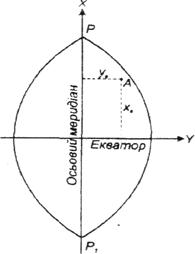
Рис. 2.7. Плоскі прямокутні координати Гаусса

Початок ординат розміщений у точці перетину екватора з осьовим меридіаном даної зони. В цій системі положення точки А на площині визначається плоскими прямокутними координатами ХА та УА, які називають координатами Гаусса. Тобто, плоскими прямокутними координатами точки А (ХА;УА) в системі координат Гаусса-Крюгера називають відстані від осей координат (екватора і осьового меридіана зони відповідно), які і характеризують положення точки А на земній поверхні.

У кожній зоні координати X та У можуть бути як від'ємні, так і додатні за значенням. Абсциси вважають додатними, якщо відраховуються від екватора на північ і від'ємними, якщо на південь. Ординати, які відраховуються від осьового меридіана на схід, вважають додатними, а на захід - від'ємними.

У системі координат Гаусса-Крюгера для всіх точок на території України абсциси мають додатні значення, а для того, щоб позбутися від'ємних значень в ординатах, прийнято умовно вважати ординату осьового меридіана рівну не нулю, а +500 км, при цьому, попереду ординати обов'язково вказують номер зони.

4.2. Картографічні проекції

Картографічна проекція - це математично певне відображення поверхні еліпсоїда або кулі (глобуса) на площину карти. Карти світу зазвичай складають в циліндричних, псевдоциліндричних і поліконічних проекціях (мал. 4.12). Для зменшення спотворень часто використовують січні циліндри, а псевдоциліндричні проекції іноді дають з розривами на океанах.

Карти півкуль завжди будують в азимутних проекціях. Для західного і східного півкуль природно брати поперечні (екваторіальні), для північного і південного півкуль - нормальні(мал. 4.13), а в інших випадках (наприклад, для Материкового і океанічного півкуль) - косі азимутні проекції.

Карти материків Європи, Азії, Північної Америки, Південної Америки, Австралії з Океанією найчастіше будують в рівновеликих косих азимутних проекціях, для Африки беруть поперечні, а для Антарктиди - нормальні азимутні. Карти окремих країн, адміністративних областей, провінцій, штатів виконують в косих рівнокутних і рівновеликих конічних або азимутних проекціях, але багато що залежить від конфігурації території і її положення на земній кулі. Для невеликих по площі районів завдання вибору проекції втрачає актуальність, можна використовувати різні рівнокутні проекції, маючи на увазі, що спотворення площ на малих територіях все одно майже неощутимы.

Топографічні карти Росії створюють в поперечно-циліндричній проекції Гаусса-Крюгера, а США і багато інших західних країн - в універсальній поперечно-циліндричній проекції Меркатора (скорочено иТМ). Обидві проекції близькі за своїми властивостями; по суті та і інша є багатосмуговими.

Морські і аеронавігаційні карти завжди даються виключно в циліндричній проекції Меркатора, а тематичні корти морів і океанів створюють в найрізноманітніших, іноді Досить складних проекціях. Наприклад, для спільного показу Атлантичного і Північного Льодовитого океанів застосовують особливі проекції з овальними изоколами, а для зображення усього Світового океану - рівновеликі проекції з розривами на мате-

Розпізнати проекцію, в якій складена карта, - означає встановити її назву, визначити приналежність до того або іншого виду, класу. Це треба для того, щоб мати уявлення про властивості проекції, характер, розподіл і величину спотворень - словом, для того, щоб знати, як користуватися картою, чого від неї можна чекати.

Деякі нормальні проекції відразу розпізнаються по виду меридіанів і паралелей. Наприклад, легко впізнанні нормальні циліндричні, псевдоциліндричні, конічні, азимутні проекції. Але навіть досвідчений картограф не відразу розпізнає багато довільних проекцій, буде потрібно спеціальні виміри по карті, щоб виявити їх равноугольность, равновеликость або равнопромежуточность по одному з напрямів. Для цього існують особливі прийоми: спершу встановлюють форму рамки (прямокутник, коло, еліпс), визначають, як зображені полюсы, потім вимірюють відстані між сусідніми паралелями уподовж по меридіану, площі сусідніх клітин сітки, кути перетину меридіанів і паралелей, характер їх кривизни і тому подібне

Існують спеціальні таблиці-визначники проекцій для карт світу, полущарий, материків і океанів. Провівши необхідні виміри по сітці, можна відшукати в такій таблиці назву проекції. Це дасть уявлення про її властивості, дозволить оцінити можливості кількісних визначень по цій карті, вибрати відповідну карту з изоколами для внесення поправок.

4.7 Координатні сітки

Координатні сітки - важливий елемент математичної основи карт. Вони потрібні для орієнтування по карті, визначення напрямів (азимутів, румбів, кутів дирекцій), прокладення маршрутів, нанесення елементів змісту, нанесення нових об'єктів по їх координатах і зняття з карти координат об'єктів. Крім того, наявність сітки дозволяє судити про масштаб карти, про вид проекції і розподіл спотворень в ній. Сітка робить карту картою, говорять навіть, що "карта без сітки все одно що термометр без шкали". На картах використовують різні координатні сітки. Картографічна сітка - це зображення на карті ліній меридіанів і паралелей (географічної сітки), що відбивають значення довгот, рахунок яких ведеться від початкового Грінвічського меридіана, і широт, які відлічуються від екватора (мал. 4.16). Картографічна сітка має важливий географічний сенс, вона показує напрями "північ - південь" і "захід - схід", дозволяє судити про широтні пояси, про розташування об'єктів відносно країн світла. Від північного напряму меридіана за годинниковою стрілкою відлічуються географичесл<ие азимути, а різниця довгот двох пунктів виражає різницю їх часу. Лінії географічної сітки на картах наносять зазвичай через рівні інтервали: декілька десятків градусів, декілька градусів, хвилин і навіть секунд - усе залежить від масштабу і призначення карти.

Сітка прямокутних координат (прямокутна сітка) - стандартна система взаємно перпендикулярних ліній, проведених через рівні відстані, наприклад через певне число кілометрів (звідси назва - кілометрова сітка, або еетка кілометрових квадратів). Зазвичай ця сітка наноситься на топографічні карти і плани, її вертикальні лінії йдуть Паралельно осьовому меридіану геодезичної зони (вісь абсцис), ^ горизонтальні - паралельно екватору (вісь ординат); вони оциф- рованы через кілометр, а кілометрова рамка карти має більше дробові ділення (мал. 4.17). Така сітка зручна для геодезичних обчислень: визначення прямокутних координат, відстаней, кутів дирекцій і тому подібне

Сетка-указательница - будь-яка сітка на карті, призначена для вказівки місця розташування і пошуку об'єктів. Осередки такої сітки позначаються буквами і цифрами (допустимо, В- 3), і це зручно, наприклад, для відшукування населених пунктів по їх назвах, що містяться в алфавітному географічному покажчику. Зазвичай сетки-указательницы наносяться на карти атласів, а у кінці приводиться список назв усіх об'єктів, поміщених в атласі.

Можна зустріти і інші координатні сітки. На старовинних морських картах - портоланах зображалася сітка компасних ліній, на деяких французьких картах досі дається сітка градів (коло складає 400 градів, а кожен град містить 100 метричних хвилин). Деякі країни використовують власні системи прямокутних координат і відповідно - свої координатні сітки.

4.8. Разграфка, номенклатура " і рамки карти

Разграфка, або нарізка карти, - це система ділення много-листной карти на листи. Найчастіше застосовуються два види разграфки: трапецієвидна, при якій межами листів служать меридіани і паралелі, і прямокутна, коли карта ділиться на прямокутні або квадратні листи однакового розміру.

Серії державних топографічних і тематичних карт, включаючі тисячі листів, мають в кожній країні стандартну разграфку. Наприклад, в Росії в основу разфафки топографічних карт покладена карта в масштабі 1:1 ТОВ ТОВ, будь-який її лист є трапецією, яка обмежена меридіанами, проведеними через 6°, і паралелями, проведеними через 4°. Разграфку карт більших масштабів отримують, ділячи лист мільйонної карти на частини. У одному листі мільйонної карти міститься чотири листи карти в масштабі 1:500 ТОВ, 36 листів карти в масштабі 1:200 ТОВ (мал. 4.18) і так далі

Особливий спосіб разграфки застосований для міжнародної карти в масштабі 1:2 500 ТОВ (мал. 4.19). Поверхня Земної кулі розділена на шість зон (три - на північ і три - на південь від екватора). Чотири зони дано в равнопромежуточной конічних, а дві приполярні - в равнопромежуточной азимутній проекціях. Всього карта включає 224 листи плюс 38 окремих компактних районів, що перекриваються для цілісного зображення, і країн.

При прямокутній разграфке карта нарезается на листи однакового формату, це зручно для друкування карт, поєднання їх по загальних рамках, склеювання або брошурування.

В деяких випадках для зручності користування картами разграфка дається з більш менш значними перекриттями листів. Наприклад, морські навігаційні карти перекриваються на величину до 10 см (мал. 4.20) - це зроблено для зручності прокладення курсу судна на суміжних листах.

З разграфкой безпосередньо пов'язана номенклатура, тобто система позначення листів в багатолистих серіях карт. Для топографічних і оглядово-топографічних карт встановлена єдина державна система номенклатури, яка починається з мільйонної карти і далі послідовно нарощується. Номенклатура тематичних карт може співпадати з топографічними або бути довільною, наприклад, листи гіпсометричної карти Росії з суміжними країнами в масштабі 1:2 500 ТОВ позначаються порядковими номерами.

Схема разграфки зазвичай дається на спеціальному збірному листі. На нім показують контури території, много-листной картою, що покривається, розподіл на окремі листи і номенклатру цих листів.

Відповідно до разграфкой міняється і форма рамок карт: вони можуть бути трапецієвидними або прямокутними. Крім того, рамки карти можуть бути представлені у вигляді кіл (наприклад, для карт півкуль) і еліпсів (карти світу в псевдоциліндричних проекціях). Прийнято розрізняти внутрішню рамку, що безпосередньо обмежує картографічне зображення, градусну і хвилинну, на які відповідно наносять градусні і (чи) хвилинні поділки по широті і довготі, а також зовнішню рамку - вона охоплює усю карту, облямовує усі інші рамки і має декоративне значення.

4.9. Компонування

Компонуванням карти називається розміщення самого картографічного зображення, назви карти, легенди, врізань і інших даних усередині рамки, на полях карти або в межах листа. Компонування вважається вдалим, якщо усі елементи карти розміщені доцільно, досить компактно, але нескупчено, ними зручно користуватися, - словом, простір карти раціонально організований і зображення зорово урівноважене.

Підібрати хороше компонування не завжди просто, це вимагає деякого дизайнерського досвіду і художнього смаку. Доводиться враховувати багато чинників: проекцію карти, форму зображуваної території (акваторії) і її орієнтування усередині рамки, необхідність показу сусідніх територій, розмір легенди, бажаність розміщення карт-врізань, додаткових графіків, діаграм і тому подібне

Особливо багато проблем виникає при картофафировании територій із складною некомпактною конфігурацією. Тоді видалена частина території може даватися у врізанні (наприклад, на карті європейської частини Росії у врізання часто поміщають далеко віддалені острови Нової Землі). У інших випадках виступаючі частини території, що картографується, виводяться в розриви рамки. Іноді у врізанні повторюється та ж територія, але в зменшеному масштабі - на ній дається допоміжна карта. Зустрічаються і так звані "плаваючі" компонування, коли на одному листі вільно без рамок розміщуються декілька територій (чи одна територія кілька разів). Залежно від конфігурації території выби- рают вільне місце для розміщення назви карти, легенди, масштабу усередині рамки або ж виносять їх за рамку - варіанти дизайнерських рішень дуже різноманітні.

Дата добавления: 2014-01-07