
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Замена переменной в интеграле
|
|
|
|
Наибольшее число известных интегралов вычисляются с использованием этого приема. Суть его в следующем. Вместо прежней переменной интегрирования вводится новая переменная так, чтобы вновь получившийся интеграл стал более простым, или более удобным для интегрирования. Основан этот прием на свойстве инвариантности первого дифференциала функции.
Рассмотрим интеграл  . Очевидно, его можно представить в виде
. Очевидно, его можно представить в виде 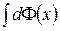 , где
, где 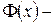 неизвестная пока первообразная подынтегральной функции
неизвестная пока первообразная подынтегральной функции 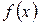 . Пусть
. Пусть  . Из инвариантности первого дифференциала имеем с одной стороны
. Из инвариантности первого дифференциала имеем с одной стороны 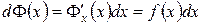 , с другой
, с другой
 ,
,
откуда следует, что вместо интеграла  можно вычислять интеграл
можно вычислять интеграл
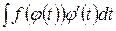 . После вычисления полученного интеграла необходимо вернуться к старой переменной. Итак,
. После вычисления полученного интеграла необходимо вернуться к старой переменной. Итак,
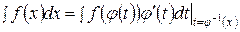 ,
,
где  функция, обратная функции
функция, обратная функции  .
.
Примеры.
1. 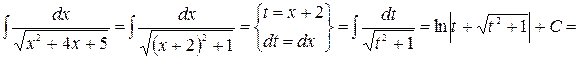
 .
.
После выделения полного квадрата в подкоренном выражении стала очевидной замена, приводящая интеграл к табличному. Замена приведена в фигурных скобках. Важно отметить, что в ходе замены должна быть установлена связь не только между новой и старой переменными, но и между дифференциалами этих переменных.
Необходимо заметить, что в первой строке осуществлена, вообще говоря, неверная запись результата, в результате которой вычисленный интеграл представлен в виде функции 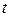 , хотя он является функцией
, хотя он является функцией 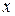 , что подтверждается второй строкой решения после проведения обратной замены. В большинстве учебников такая вольность промежуточных вычислениях считается допустимой в, однако, ответ должен быть функцией старой переменной. Это продемонстрировано во втором и третьем примерах.
, что подтверждается второй строкой решения после проведения обратной замены. В большинстве учебников такая вольность промежуточных вычислениях считается допустимой в, однако, ответ должен быть функцией старой переменной. Это продемонстрировано во втором и третьем примерах.
2.  .
.
3.  .
.
Следует заметить, что при вычислении практически каждого интеграла используется формула дифференциала функции 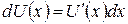 . Без знания этой формулы вычисление интегралов невозможно.
. Без знания этой формулы вычисление интегралов невозможно.
В вышеприведенных примерах не всегда понятно, как выбирается замена переменной. Далее будет изложена теория, из которой следует, какую замену нужно производить в том, или ином случае.
Примеры для самостоятельного решения
Вычислить интегралы
7. 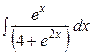 , 8.
, 8. 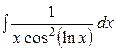 , 9.
, 9.  ,
,
10. 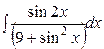 , 11.
, 11.  , 12.
, 12. 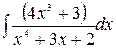 ,
,
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 352; Нарушение авторских прав?; Мы поможем в написании вашей работы!