Метод коэффициентов системы линейных уравнений

Метод коэффициентов системы линейных уравнений. Идея этого метода заключается в аналитическом выявлении параметров, и в частности коэффициентов весомости тех уравнений, ко­торыми (как это предполагается) бессознательно опери­рует эксперт, когда на основе известных для r-го оценива­емого объекта значений показателей q_ir он выносит по каждому объекту комплексную оценку .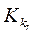

Метод применим при одновременном существование следующих условий

1) имеется априорная информация о значениях показателя 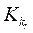и показателей Р _ir для r-х однородных объектов;

2) выборка из генеральной совокупности таких объек­тов, отобранная случайным образом, достаточно велика, во всяком случае, объем выборки не меньше i, т. е. числа тех свойств объекта, коэффициенты весомостей которых должны определяться;

3) известно, что для каждого из отобранных объектов зависимость между 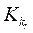и Р _ir имеет не стохастический; а функциональный характер (иначе говоря, для всех i, r коэффициент парной корреляции между 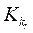и Р _ir больше чем 0,80);

4) могут быть сделаны достаточно правдоподобные предположения о характере f — функциональной зависимости

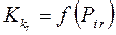
При соблюдении этих четырех условий значения коэффициентов весомости M_i могут быть определены как корни системы линейных уравнений.

Как известно, на практике зависимость 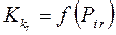в подавляющем большинстве случаев бывает одного из двух типов:

1) f есть средняя арифметическая;

2) f есть средняя геометрическая.

Рассмотрим расчетные формулы для определения значений, при­менительно к каждому из двух случаев.

1. Пусть f — средняя взвешенная арифметическая, т. е.

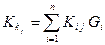
Обозначим: 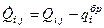и 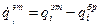. Тогда неизвестные значения коэффициентов весомости G_i могут быть получены при решении

Системы линейных алгебраических уравнений:

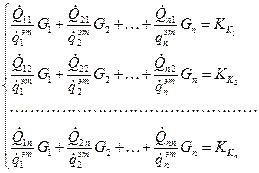
(методы их решений общеизвестны и описаны в любом справочнике по алгебре).

2. Пусть f — средняя взвешенная геометрическая, т. е.

,

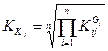Тогда G_i могут быть найдены как корни системы линейных алгебраических уравнений:

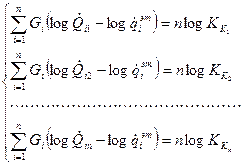
Дата добавления: 2014-01-07