С помощью степенных рядов

Приближенное вычисление значений функций и определенных интегралов

Разложение функций в степенные ряды с успехом применяется для решения различных задач, например:

- вычисление сумм числовых рядов;

- вычисление значений аналитических функций;

- вычисление интегралов (определенных и несобственных);

- вычисление пределов функций;

- решение некоторых типов алгебраических уравнений;

- решение некоторых типов дифференциальных уравнений.

Вычисление искомой величины сводится к приближенному вычислению суммы S некоторого сходящегося числового ряда. Если требуется вычислить S с заданной точностью e>0, то тем или иным способом подбирают номер n так, чтобы выполнялось условие , где S_n ¾ это n -я частичная сумма, а R_n ¾ n -й остаток числового ряда. Тогда 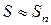с точностью до e>0.

Для знакочередующегося ряда типа Лейбница имеем .

Для положительного ряда оценка погрешности при приближенном вычислении суммы значительно сложнее. Один из основных методов в таком случае ¾ это замена остатка ряда геометрическим рядом с большей суммой.

Задача 1. Вычислить , используя разложение подынтегральной функции в ряд Маклорена. Взять три члена разложения. Оценить погрешность.

Решение. Используя известное разложение функции ln(1+ x) в степенной ряд, получаем: .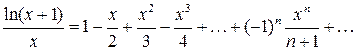

Применяя теорему о почленном интегрировании на отрезке [0;0,1], лежащем в интервале сходимости (-1;1) полученного степенного ряда, и вычисляя определенные интегралы по формуле Ньютона-Лейбница, выражаем данный интеграл как сумму числового ряда:

.

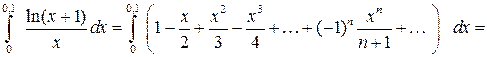
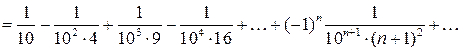Получаем 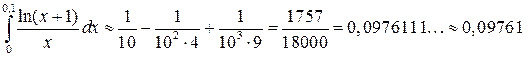, т.к. погрешность при приближенном вычислении суммы знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница, не превышает абсолютной величины первого отброшенного члена .

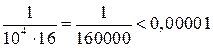Ответ. .

Замечание. Известно, что .

Задача 2. Вычислить 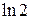с точностью до 0,001.

Решение. Используя известное разложение в степенной ряд функции получаем: 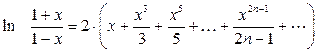, где x Î(-1;1).

При получаем: .

Следовательно, остаток ряда

. Ясно, что R_n <10^-3, если .

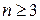Итак, .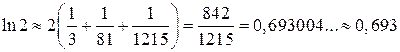

Ответ. 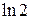»0,693 с точностью до 0,001. ().

Министерство образования и науки РФ

Негосударственная образовательная организация высшего профессионального образования

некоммерческое партнерство

«Тульский институт экономики и информатики»

Кафедра «Наименование кафедры»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ПРАКТИЧЕСКИМ (СЕМИНАРСКИМ) ЗАНЯТИЯМ

ПО дисциплине: «Математика»

Специальность: 230700 «Прикладная информатика»

Формы обучения (очная)

Тула 2011г.

Методические указания по СРС составлены доцентом, к.т.н.Липатовой И.Е. и обсуждены на заседании кафедры «Естестест в еннонаучных и гуманитарных дисциплин протокол № от " " 20 г.

Зав. кафедрой________ Е.А. Вишнякова

Методические указания по СРС пересмотрены и утверждены на заседании кафедры название кафедры факультета название факультета.

протокол №___ от "_______ "____ 20 г.

Зав. кафедрой________ Е.А. Вишнякова

Дата добавления: 2014-01-07