Знакопеременные ряды. Абсолютная и условная сходимость рядов

Определение 1. Если сходится ряд , то ряд называется абсолютно сходящимся.

Теорема 1. Если сходится ряд , то ряд также сходится.

Например, ряд является абсолютно сходящимися, так как ряд сходится по признаку сравнения, ибо для любого n Î N, а ряд сходится (a =2>1).

Абсолютно сходящиеся ряды имеют ряд важных свойств, которыми обладают конечные суммы чисел:

- слагаемые можно переставлять местами;

- слагаемые можно группировать разными способами;

- суммы рядов можно перемножать.

Определение 2. Ряд называется перестановкой ряда , если существует биекция 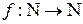такая, что 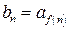для любого n Î N.

Теорема 2. Если ряд абсолютно сходится, то сходится, и притом абсолютно, любая перестановка данного ряда, и их суммы совпадают.

Определение 3. Если ряд сходится, а ряд расходится, то ряд называется условно сходящимся.

Ряд 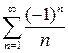является условно сходящимся. Действительно, ряд 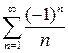сходится (по теореме Лейбница), а ряд расходится.

Теорема 3 (Римана). Если числовой ряд условно сходится, то для любого существует такой числовой ряд , полученный перестановкой членов ряда , что ряд сходится и его сумма равна C.

Дата добавления: 2014-01-07