Неравенство Чебышева и его частные случаи для случайной величины, распределенной по биномиальному закону, и для частости события

Лемма Чебышева (неравенство Маркова)

Теорема 1. Если случайная величина Х принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числа e верно неравенство

.

Доказательство. Пусть Х ¾ дискретная случайная величина, имеющая ряд распределения

X:	x 1	x 2	¼	xi	¼	xn
p 1	p 2	¼	pi	¼	pn

Пусть значения x ₁, x ₂, ¼, x_k не превосходят e, а значения x_{k +1}, ¼, x_n больше e.

По теореме сложения вероятностей .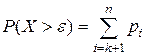

Но 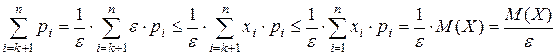. Это вытекает из неотрицательности случайной величины Х и определения математического ожидания. Следовательно, . Теорема доказана.

Теорема 2. Для любой случайной величины Х, имеющей математическое ожидание и дисперсию, справедливо неравенство Чебышева:

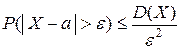, где a = M (X), e >0.

Доказательство. Применим лемму Чебышева к случайной величине 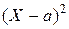и положительному числу e ². Получим неравенство 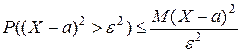, равносильное неравенству 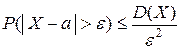. Теорема доказана.

Замечание. События ½ X - a ½>e£ и ½ X - a ½£e противоположны, следовательно:

.

Запишем неравенство Чебышева для некоторых типов случайных величин.

1. Для случайной величины Х = m, имеющей биномиальный закон распределения с математическим ожиданием np и дисперсией npq, справедливо неравенство:

.

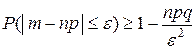2. Для частости 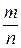события в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью , и имеющей дисперсию 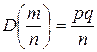, справедливо неравенство:

.

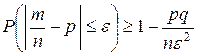Дата добавления: 2014-01-07