Гомоморфизмы колец

Определение 4.6.1. Пусть и 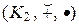– два кольца. Всякая функция f: K ₁ ® K ₂ и обладающая свойствами:

1) f (a + b) = f (a)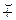 f (b),

2) f (a × b) = f (a) · f (b)

для " a, b Î K ₁, – называется гомоморфизмом колец.

Определение 4.6.2. Инъективный гомоморфизм колец называется мономорфизмом (вложением), сюръективный – эпиморфизмом, биективный – изоморфизмом. Всякий гомоморфизм f: K ® K называют эндоморфизмом кольца K, а взаимно однозначный эндоморфизм – автоморфизмом.

Изоморфные кольца будем обозначать 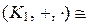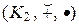или .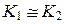

Несложно видеть, что отношение изоморфизма на множестве всех колец является отношением эквивалентности: оно рефлексивно, симметрично и транзитивно. Таким образом, все множество колец разбивается на непересекающиеся классы попарно изоморфных объектов. Важной задачей теории колец является классификация всех колец с точностью до изоморфизма.

Пример 4.6.1. Аннулятор кольца K: f (a) = 0 для всякого a Î K – тривиальный пример эндоморфизма произвольного кольца K. Другой тривиальный пример эндоморфизма – тождественное преобразование e_K любого кольца K. ·

Пример 4.6.2. Пусть С – поле комплексных чисел, f: C ® C. Для каждого z = a + bi из C положим f (z) = a – bi = . Очевидно, операция сопряжения взаимно однозначна и обладает свойствами 1 и 2 из определения гомоморфизма. Следовательно, f – автоморфизм поля комплексных чисел, причем f ² = e _C. ·

Определение 4.6.3. Пусть f: K ₁ ® K ₂ – гомоморфизм колец. Образом гомоморфизма f: K ₁ ® K ₂ называется множество = = E (f) (иногда еще обозначается ). Ядром гомоморфизма f называется множество 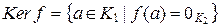, где – нейтральный элемент группы .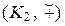

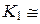Очевидно, что когда мономорфизм колец, Im f.

Пример 4.6.3. Пусть (P, +, ×) – произвольное поле и g (x) – неприводимый над P многочлен степени n из P [ x ]. Тогда по следствию 2 из теоремы 4.5.2 факторкольцо (P [ x ]/< g (x) >, Å, Ä) является полем. Несложно проверить, что функция f: P ® P [ x ]/< g (x) >, где f (a) = (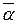) для всех a Î P, – мономорфизм данных полей. Следуя рассуждениям в конце §4.5, (P, +, ×) @ (, Å, Ä), так как Im f = . Значит, (P, +, ×) с точностью до изоморфизма отождествляется с подполем в (P [ x ]/< g (x) >, Å, Ä).

Дата добавления: 2014-01-07