
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства гомоморфизмов колец
|
|
|
|
1. Композиция гомоморфизмов колец – гомоморфизм колец.
 Пусть
Пусть  ,
, 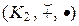 ,
,  – кольца,
– кольца,  ,
,  – гомоморфизмы колец,
– гомоморфизмы колец,  – композиция функций. Тогда для " a, b Î K 1 выполняются равенства:
– композиция функций. Тогда для " a, b Î K 1 выполняются равенства:
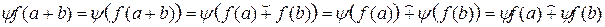 ;
;
 .
.
Итак,  – гомоморфизм колец.
– гомоморфизм колец.
2. Если f: K 1 ® K 2 – гомоморфизм колец, то 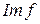 – подкольцо K 2.
– подкольцо K 2.
 Im f Í K 2 и
Im f Í K 2 и  . (K 1, +) и (K 2,
. (K 1, +) и (K 2, 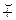 ) – группы, f – гомоморфизм данных аддитивных групп. Поэтому, по свойству 2 гомоморфизмов групп
) – группы, f – гомоморфизм данных аддитивных групп. Поэтому, по свойству 2 гомоморфизмов групп 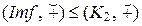 . Для
. Для 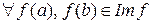 выполняется
выполняется  , поскольку f – гомоморфизм колец. Следовательно, Im f – подкольцо K 2.
, поскольку f – гомоморфизм колец. Следовательно, Im f – подкольцо K 2.
3. Если f: K 1 ® K 2 – гомоморфизм колец, то 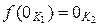 и
и  для
для 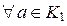 .
.
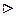 Так как f: K 1 ® K 2 – гомоморфизм соответствующих аддитивных групп колец (K 1, +) и (K 2,
Так как f: K 1 ® K 2 – гомоморфизм соответствующих аддитивных групп колец (K 1, +) и (K 2, 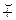 ), то по свойству 2 гомоморфизмов групп имеем
), то по свойству 2 гомоморфизмов групп имеем 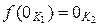 и
и  для
для 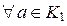 . Непосредственное доказательство:
. Непосредственное доказательство:
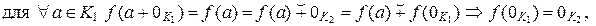

по определению гомоморфизма, нейтрального и противоположного элемента аддитивной группы.
4. Если f: K 1 ® K 2 – гомоморфизм колец, то  и для
и для 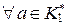
 в Im f, где
в Im f, где 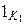 – единица K 1 и
– единица K 1 и 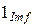 – единица Im f.
– единица Im f.
 Согласно свойству 2
Согласно свойству 2  . Если
. Если 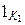 – единица K 1, то для
– единица K 1, то для  , поскольку f – гомоморфизм, выполняется
, поскольку f – гомоморфизм, выполняется

То есть  – единица
– единица 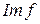 . Для
. Для 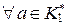 выполняются равенства
выполняются равенства 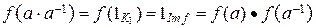 и
и  f (a –1) · f (a), следовательно,
f (a –1) · f (a), следовательно,  в Im f.
в Im f. 
5. Если f: K 1 ® K 2 – гомоморфизм колец, то Ker f – двусторонний идеал K 1.
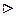 Ker f Í K 1 и Ker f ¹ Æ, так как
Ker f Í K 1 и Ker f ¹ Æ, так как  Ker f по свойству 3. Для " a, b Î Ker f
Ker f по свойству 3. Для " a, b Î Ker f  . Далее, для " a Î Ker f, " k Î K 1 выполняется
. Далее, для " a Î Ker f, " k Î K 1 выполняется 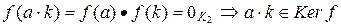 ,
,  . Итак,
. Итак, 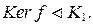

Пример 4.6.4. Рассмотрим функцию f: Z /28 Z ® Z /28 Z, где 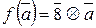 . f – эндоморфизм кольца (Z /28 Z, Å, Ä), так как для любых
. f – эндоморфизм кольца (Z /28 Z, Å, Ä), так как для любых 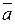 ,
,  Î Z /28 Z
Î Z /28 Z
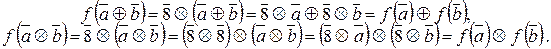
 ,
,  .
.
Можно заметить, что  для
для 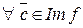 , поскольку
, поскольку  , а также, что Im f и Ker f являются главными идеалами кольца Z /28 Z, то есть Im f
, а также, что Im f и Ker f являются главными идеалами кольца Z /28 Z, то есть Im f  , где (k, 28) = 28/7 = 4, и Ker f
, где (k, 28) = 28/7 = 4, и Ker f  , где (l, 28) = 28/4 = 7. Таким образом,
, где (l, 28) = 28/4 = 7. Таким образом,
Im f 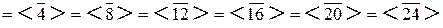 ,
,
Ker f  .
.
Im f – подкольцо Z /28 Z, но 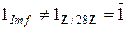 , поскольку
, поскольку 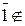 Im f. ·
Im f. ·
6. Гомоморфизм колец f: K 1 ® K 2 является мономорфизмом тогда и только тогда, когда  .
.
 Доказательство вытекает из свойства 4 гомоморфизмов групп, поскольку f: K 1 ® K 2 – гомоморфизм соответствующих групп (K 1, +) и (K 2,
Доказательство вытекает из свойства 4 гомоморфизмов групп, поскольку f: K 1 ® K 2 – гомоморфизм соответствующих групп (K 1, +) и (K 2, 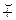 ).
).
Из свойств 5 и 6 следует, что любой гомоморфизм произвольных полей является либо нулевым, либо инъективным (так как поле не имеет нетривиальных идеалов). Гомоморфизмы позволяют произвести отождествления изоморфных полей, установить между полями отношения частичного порядка – по включению.
Теорема 4.6.1 (первая теорема о гомоморфизмах колец). Пусть (K, +, ×) – кольцо,  – двусторонний идеал. Тогда существует эпиморфизм колец
– двусторонний идеал. Тогда существует эпиморфизм колец 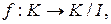 для которого Ker f = I.
для которого Ker f = I.
 Построим функцию
Построим функцию 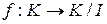 , где
, где  . f – сюръекция:
. f – сюръекция:  ,
, 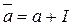 , существует
, существует  .
.

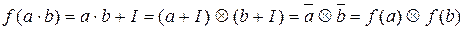
для  согласно построению факторкольца (K / I, Å, Ä). Поэтому f – гомо-морфизм колец.
согласно построению факторкольца (K / I, Å, Ä). Поэтому f – гомо-морфизм колец.
Для  Ker f. Пусть
Ker f. Пусть 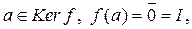 но если
но если  , так как различные классы вычетов по модулю двустороннего идеала не пересекаются. Получается противоречие. Значит,
, так как различные классы вычетов по модулю двустороннего идеала не пересекаются. Получается противоречие. Значит, 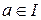 и
и  . Итак,
. Итак, 

Определение 4.6.4. Гомоморфизм колец 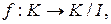 где
где 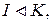 при ко-тором
при ко-тором 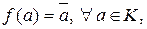 называется естественным (каноническим) гомомор-физмом.
называется естественным (каноническим) гомомор-физмом.
Теорема 4.6.2 (вторая теорема о гомоморфизмах колец). Пусть – гомоморфизм кольца
– гомоморфизм кольца  в кольцо
в кольцо 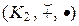 . Тогда
. Тогда 
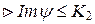 (свойство 2 гомоморфизмов колец),
(свойство 2 гомоморфизмов колец), 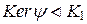 (свойство 5 гомоморфизмов колец). Построим функцию f:
(свойство 5 гомоморфизмов колец). Построим функцию f: 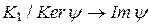 , где
, где 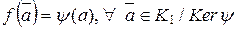 . f – сюръективная функция, так как для
. f – сюръективная функция, так как для 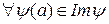
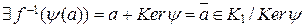 .
.
f не зависит от выбора представителя класса вычетов 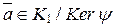 : пусть a 1 = a + i
: пусть a 1 = a + i  , тогда получаем, что
, тогда получаем, что
 .
.
Пусть  , тогда
, тогда  . Так как иначе
. Так как иначе 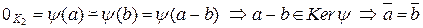 , что приводит к противоречию тому, что
, что приводит к противоречию тому, что 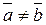 . Значит, f – инъекция. Итак, f:
. Значит, f – инъекция. Итак, f: 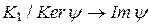 – биективная функция.
– биективная функция.
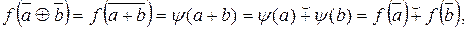

для 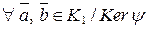 . Значит, f – гомоморфизм колец. Таким образом, f – изоморфизм колец
. Значит, f – гомоморфизм колец. Таким образом, f – изоморфизм колец 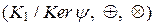 и
и 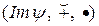 .
.
Поскольку для произвольного кольца 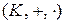
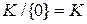 , из свойства 6 гомоморфизмов колец и теоремы 4.6.2 следует, что любой инъективный эндоморфизм кольца является автоморфизмом. В частности, любой ненулевой эндоморфизм поля является его автоморфизмом.
, из свойства 6 гомоморфизмов колец и теоремы 4.6.2 следует, что любой инъективный эндоморфизм кольца является автоморфизмом. В частности, любой ненулевой эндоморфизм поля является его автоморфизмом.
Пример 4.6.5. Пусть (P, +, ×) – поле, (P [ x ], +, ×) – кольцо полиномов над полем P.  – фиксированный элемент поля. Рассмотрим функцию
– фиксированный элемент поля. Рассмотрим функцию 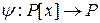 , где
, где 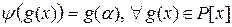 . Тогда для
. Тогда для 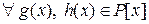 справедливы равенства:
справедливы равенства:
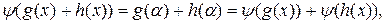

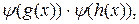
следовательно, y – гомоморфизм колец.
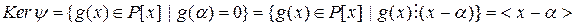 по следствию 1 из теоремы Безу 4.4.4. y – сюръекция, так как для
по следствию 1 из теоремы Безу 4.4.4. y – сюръекция, так как для 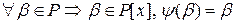 и
и  . Значит,
. Значит, 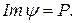 Таким образом, по теореме 4.6.2
Таким образом, по теореме 4.6.2  . ·
. ·
Развитием следствия 2 из теоремы 4.5.2 является следующая теорема.
Теорема 4.6.3 (теорема существования корня). Для всякого неприводимого полинома f (x)Î P [ x ] степени n Î N существует расширение поля P, содержащее корень этого полинома и изоморфное полю P [ x ]/< f (x) >.
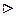 Факторкольцо (P [ x ]/< f (x) >, Å, Ä) является полем согласно следствию 2 из теоремы 4.5.2. Подполе
Факторкольцо (P [ x ]/< f (x) >, Å, Ä) является полем согласно следствию 2 из теоремы 4.5.2. Подполе 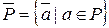 в P [ x ]/< f (x) > изоморфно полю P, очевидно, изоморфизм задает функция y: P ® P [ x ]/< f (x) >, где y (a) =
в P [ x ]/< f (x) > изоморфно полю P, очевидно, изоморфизм задает функция y: P ® P [ x ]/< f (x) >, где y (a) = 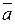 , являющаяся вложением P в P [ x ]/< f (x) >, как уже говорилось в примере 4.6.3. Пусть f (x) = anxn +…+ a 1 x + a 0,
, являющаяся вложением P в P [ x ]/< f (x) >, как уже говорилось в примере 4.6.3. Пусть f (x) = anxn +…+ a 1 x + a 0,  , тогда в поле P [ x ]/< f (x) >
, тогда в поле P [ x ]/< f (x) > 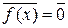 . Но поскольку
. Но поскольку 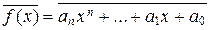 =
= 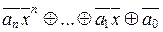 , то,
, то,  является корнем полинома
является корнем полинома 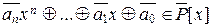 . Рассмотрим теперь множество S, удовлетворяющее условиям: S Ç P = Æ, | S | = | (P [ x ]/< f (x) >)\
. Рассмотрим теперь множество S, удовлетворяющее условиям: S Ç P = Æ, | S | = | (P [ x ]/< f (x) >)\ | ¹ 0 при n > 1. Пусть F = S È P, при n = 1 F = P. Зададим на F структуру поля, продолжив мономорфизм y до изоморфизма F на P [ x ]/< f (x) >. Если b, c Î F, то полагаем
| ¹ 0 при n > 1. Пусть F = S È P, при n = 1 F = P. Зададим на F структуру поля, продолжив мономорфизм y до изоморфизма F на P [ x ]/< f (x) >. Если b, c Î F, то полагаем
b + c = y –1(y (b)Å y (c)), b × c = y –1(y (b)Ä y (c)).
При ограничениях на P эти операции совпадают соответственно с заданными операциями сложения и умножения в P, и ясно, что P – подполе F. Положим a =  , тогда y (f (a)) = y (anan +…+ a 1 a + a 0) =
, тогда y (f (a)) = y (anan +…+ a 1 a + a 0) =  = =
= =  и, поскольку y – изоморфизм F на P [ x ]/< f (x) >, f (a) = 0 в поле (F, +, ×). Значит, построенное поле является расширением поля P, содержащим корень a полинома f (x).
и, поскольку y – изоморфизм F на P [ x ]/< f (x) >, f (a) = 0 в поле (F, +, ×). Значит, построенное поле является расширением поля P, содержащим корень a полинома f (x).
Следствие 1. Для любого полинома f (x)Î P [ x ] степени n Î N существует расширение поля P, содержащее корень этого полинома.
 По теореме 4.4.1 полином f (x) однозначно разлагается на множители: f (x) =
По теореме 4.4.1 полином f (x) однозначно разлагается на множители: f (x) = 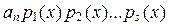 , где
, где 
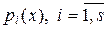 , – неприводимые над P полиномы со старшими коэффициентами, равными 1,
, – неприводимые над P полиномы со старшими коэффициентами, равными 1,  – старший коэффициент f (x). Согласно теореме 4.6.3 для каждого
– старший коэффициент f (x). Согласно теореме 4.6.3 для каждого 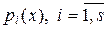 существует расширение поля P, содержащее корень данного полинома, являющийся и корнем полинома f (x) в соответствии со следствием 1 из теоремы Безу 4.4.4 и свойством 3 делимости полиномов.
существует расширение поля P, содержащее корень данного полинома, являющийся и корнем полинома f (x) в соответствии со следствием 1 из теоремы Безу 4.4.4 и свойством 3 делимости полиномов.
Замечание. Тот факт, что расширение  поля P содержит корень a полинома f (x)Î P [ x ], вовсе не означает, что
поля P содержит корень a полинома f (x)Î P [ x ], вовсе не означает, что  содержит все корни этого полинома.
содержит все корни этого полинома.
Пример 4.6.6. Полином f (x) = x 4–2 неприводим над Q по по признаку Эйзенштейна: p = 2. В поле C данный полином имеет четыре простых корня: 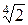 ,
, 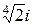 ,
,  и
и  . Но поле
. Но поле 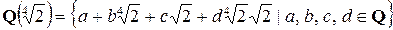 содержит только первый и третий из этих корней, но не все четыре. ·
содержит только первый и третий из этих корней, но не все четыре. ·
Следствие 2. Для любого полинома f (x)Î P [ x ] степени n Î N существует расширение поля P, содержащее все корни f (x).
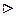 Доказательство проведем индукцией по степени полинома f (x). Если deg f = 1, то f (x) = ax + b, a ¹ 0, и – a –1 b Î P – единственный корень f (x), значит, P – искомое поле. Предположим, что утверждение верно для всех многочленов степеней, меньших фиксированного n Î N >1, с коэффициентами из произвольных полей.
Доказательство проведем индукцией по степени полинома f (x). Если deg f = 1, то f (x) = ax + b, a ¹ 0, и – a –1 b Î P – единственный корень f (x), значит, P – искомое поле. Предположим, что утверждение верно для всех многочленов степеней, меньших фиксированного n Î N >1, с коэффициентами из произвольных полей.
Пусть теперь deg f = n > 1. Тогда по следствию 1 из теоремы 4.6.3 существует расширение P 1 поля P, содержащее корень a полинома f (x). Согласно следствию 1 из теоремы 4.4.4 в P 1[ x ] f (x) = (x – a) g (x), где g (x)Î P 1[ x ] и deg g = = n –1. По предположению индукции существует расширение P 2 поля P 1, содержащее все корни g (x). Так как P 2 является расширением поля P и содержит все корни полинома f (x) (оно содержит a и все корни полинома g (x)), то P 2 и есть искомое расширение.
Теорема 4.6.4. Пусть 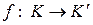 – эпиморфизм колец, Ker f = I. Тогда существует взаимно однозначное и сохраняющее включения соответствие между всеми идеалами
– эпиморфизм колец, Ker f = I. Тогда существует взаимно однозначное и сохраняющее включения соответствие между всеми идеалами  кольца
кольца  и идеалами U кольца (K, +, ×), содержащими I, такое что
и идеалами U кольца (K, +, ×), содержащими I, такое что  ,
,  .
.
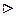
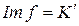 , Ker f = I. Пусть
, Ker f = I. Пусть 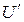 – произвольный идеал кольца
– произвольный идеал кольца  , соответственно левый, правый, двусторонний. Рассмотрим прообраз идеала
, соответственно левый, правый, двусторонний. Рассмотрим прообраз идеала  при отображении f –
при отображении f –  . Тогда для
. Тогда для 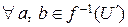 ,
,  выполняются следующие свойства:
выполняются следующие свойства:
1)  , так как
, так как 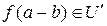 , поскольку
, поскольку 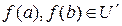 ,
,  – идеал кольца
– идеал кольца 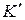 , значит,
, значит,  , а
, а  ;
;
2)  , так как
, так как  , поскольку
, поскольку 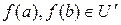 ,
,  – идеал кольца
– идеал кольца 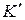 , значит,
, значит,  , а
, а 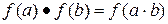 ;
;
3) 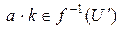 , если
, если  – левый идеал,
– левый идеал,  , если
, если  – правый идеал,
– правый идеал,  , если
, если  – двусторонний идеал, так как соответственно
– двусторонний идеал, так как соответственно  ,
, 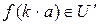 ,
, 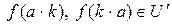 , поскольку
, поскольку 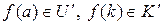 и соответственно
и соответственно  ,
,  ,
,  , а
, а 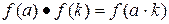 ,
, 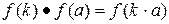 .
.
Таким образом, 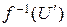 является соответственно левым, правым, двусторонним идеалом кольца (K, +, ×) согласно определению. Поскольку
является соответственно левым, правым, двусторонним идеалом кольца (K, +, ×) согласно определению. Поскольку 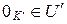 , то
, то  . Если
. Если  – идеалы кольца
– идеалы кольца 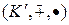 , причем
, причем  , то для
, то для  , значит, для
, значит, для 
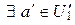 , такое что
, такое что 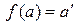 , поскольку
, поскольку 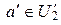 ,
, 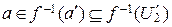 , следовательно,
, следовательно,  . Итак, существует функция, заданная на множестве всех идеалов кольца
. Итак, существует функция, заданная на множестве всех идеалов кольца 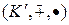 , которая каждому левому, правому, двустороннему идеалу ставит в соответствие его прообраз при отображении f, являющийся соответственно левым, правым, двусторонним идеалом кольца (K, +, ×), содержащим I, и данная функция сохраняет включения идеалов.
, которая каждому левому, правому, двустороннему идеалу ставит в соответствие его прообраз при отображении f, являющийся соответственно левым, правым, двусторонним идеалом кольца (K, +, ×), содержащим I, и данная функция сохраняет включения идеалов.
Пусть теперь U – произвольный идеал кольца (K, +, ×), соответственно левый, правый, двусторонний. Рассмотрим образ идеала U при отображении f – 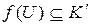 . Тогда для
. Тогда для  ,
, 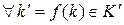 выполняются следующие свойства:
выполняются следующие свойства:
1)  , так как
, так как  , поскольку
, поскольку 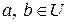 , U – идеал кольца K, значит,
, U – идеал кольца K, значит, 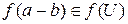 , а
, а 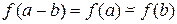 ;
;
2)  , так как
, так как 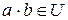 , поскольку
, поскольку 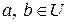 , U – идеал кольца K, значит,
, U – идеал кольца K, значит,  , а
, а 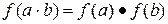 ;
;
3)  , если U – левый идеал,
, если U – левый идеал, 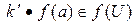 , если U – правый идеал,
, если U – правый идеал,  , если U – двусторонний идеал, так как соответственно
, если U – двусторонний идеал, так как соответственно 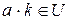 ,
,  ,
,  , поскольку
, поскольку  и соответственно
и соответственно 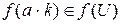 ,
,  ,
,  , а
, а 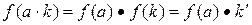 ,
, 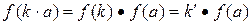 .
.
Таким образом,  является соответственно левым, правым, двусторонним идеалом кольца
является соответственно левым, правым, двусторонним идеалом кольца  согласно определению. Если
согласно определению. Если 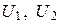 – идеалы кольца (K, +, ×), причем
– идеалы кольца (K, +, ×), причем  , то для
, то для 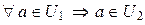 , значит, для
, значит, для 
 , такое что
, такое что 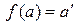 , поскольку
, поскольку 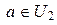 ,
, 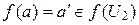 , следовательно,
, следовательно,  . Для выполнения условия
. Для выполнения условия  ,
,  , где
, где  – идеал кольца
– идеал кольца  , необходимо и достаточно, чтобы идеал U кольца (K, +, ×) содержал в качестве подмножества I.
, необходимо и достаточно, чтобы идеал U кольца (K, +, ×) содержал в качестве подмножества I.
Итак, показано, что существует взаимно однозначное и сохраняющее включения соответствие между всеми левыми, правыми, двусторонними идеалами кольца 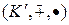 и их прообразами при отображении f, являющимися соответственно левыми, правыми, двусторонними идеалами кольца (K, +, ×), содержащими I.
и их прообразами при отображении f, являющимися соответственно левыми, правыми, двусторонними идеалами кольца (K, +, ×), содержащими I. 
Замечание. В ходе доказательства теоремы 4.6.3 было показано, что при произвольном гомоморфизме колец 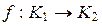 образ любого левого, правого, двустороннего идеала кольца
образ любого левого, правого, двустороннего идеала кольца  является соответственно левым, правым, двусторонним идеалом кольца
является соответственно левым, правым, двусторонним идеалом кольца 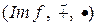 . Также было показано, что прообраз любого левого, правого, двустороннего идеала кольца
. Также было показано, что прообраз любого левого, правого, двустороннего идеала кольца 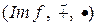 является соответственно левым, правым, двусторонним идеалом кольца
является соответственно левым, правым, двусторонним идеалом кольца  , содержащим Ker f.
, содержащим Ker f.
Следствие. При произвольном гомоморфизме колец  существует взаимно однозначное и сохраняющее включения соответствие между всеми левыми, правыми, двусторонними идеалами кольца
существует взаимно однозначное и сохраняющее включения соответствие между всеми левыми, правыми, двусторонними идеалами кольца 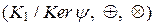 и соответственно левыми, правыми, двусторонними идеалами кольца
и соответственно левыми, правыми, двусторонними идеалами кольца 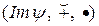 .
.
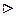 Согласно теореме 4.6.2 существует изоморфизм колец
Согласно теореме 4.6.2 существует изоморфизм колец  ,
, 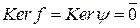 . Применяя теорему 4.6.3, получаем, что f задает требуемое взаимно однозначное соответствие между идеалами
. Применяя теорему 4.6.3, получаем, что f задает требуемое взаимно однозначное соответствие между идеалами  кольца
кольца 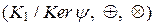 и
и  кольца
кольца 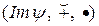 , такое что
, такое что  ,
, 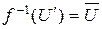 .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1696; Нарушение авторских прав?; Мы поможем в написании вашей работы!