Дискретные случайные процессы

При расчетах, оценках и прогнозировании надежности мы будем постоянно сталкиваться со случайными процессами.

Под случайным процессом будем называть процесс, который протекает таким образом, что невозможно точно предсказать реализацию его.

Реализация случайного процесса – последовательность конкретных состояний, которые возникают в процессе эксперимента.

Рассмотрим некоторую систему Х, в которой протекает случайный процесс, состоящий в том, что система с течением времени меняет свои состояния.

Обозначим эти состояния через Х (t). Конкретная реализация случайного процесса пусть будет х (t).

В качестве примера рассмотрим работу системы автоматизированного восстановления работоспособности. В некоторое время система работает, затем находится в состоянии контроля. Условимся для определенности считать, что если система в момент t не работает, то X (t) = 0, если работает, то X (t) = 1. Таким образом, реализацию случайного процесса можно представить в следующем виде (рис. 2.9).

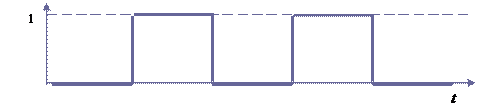Рис. 2.9

В этом примере работа САВР характеризуется одной случайной величиной Х (t), которая в любой момент t равно 0 либо 1. При этом, если система не работает трудно предсказать заранее, когда она будет функционировать в первый раз (t ₁), когда она восстановит работоспособность АСУ, когда будет инициирована вторично (t ₃) и т.д.

Случайная величина Х (t) рассматриваемая как функция времени, изменяющуюся скачкообразно в случайные моменты времени.

В качестве еще одного примера рассмотрим функционирование дуплексной вычислительной системы.

Рис. 2.10

Процесс Х (t) может случайным образом, в какие либо моменты времени t переходить из состояния в состояние.

Х ₀₀ – обе ЭВМ свободны.

Х _0,1 – первая ЭВМ функционирует, вторая свободна.

Х ₀₁ – первая ЭВМ свободная, вторая работает.

Х _1,1 – обе ЭВМ работают.

Данный пример можно рассматривать и на состояние отказов.

В данном случае физическая система может находиться в любой момент времени только в одном состоянии (0,1).

В общем виде, если ЭВМ работает, то Х (t)= Х ₀, если нет Х (t)= Х ₁.

Таким образом, мы будем рассматривать системы, которые имеют конечное или счетное множество возможных состояний.

Счетное множество – это такое множество, элементы которого можно расположить в определенной последовательности (перенумеровать). Системы с конечным множеством возможных состояний будем называть системами с дискретными состояниями. При этом будем считать, что переход системы из состояния в состояние осуществляется (мгновенно).

Рассмотрим систему с конечным числом состояний х ₀, х ₁, …, х_n. В любой момент времени может иметь место одно из (n+ 1) событий:

x (t)= x_i, i, (2.68)

которые образуют полную группу несовместимых событий. Вероятность события X (t) =X_i обозначим через P_i (t):

. (2.69)

Так как события X (t)= X_i образуют полную группу несовместимых событий, то для любого момента времени:

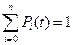. (2.70)

Таким образом, дискретным случайным процессом, X (t) называется процесс, протекающий в система с дискретным состояниями, число которых конечно. Такой процесс интерпретируется с помощью графа возможных состояний с указанием возможных переходов из состояния в состояние (рис. 2.11).

Рис. 2.11

Дата добавления: 2014-01-07