
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Отказы в невостанавливаемых системах
|
|
|
|
Ошибки, порождаемые неисправностями логических и специальных элементов
Имеющийся статистический материал показывает, что сбои составляют большую часть общего числа нарушения работоспособности систем: внезапные и постепенные отказы 0,5-4,5%, сбои 55-95,5%.
Для обнаружения нарушений работоспособности в системах широко используют различные методы контроля, позволяющие зафиксировать наиболее типичные. Сбои, зафиксированные системой контроля, исправляют, и тем самым не допускается распространение их на выход системы.
Сегодня самая серьезная проблема в сфере обработки информации – это проблема дефектов программного обеспечения. В качестве подтверждения этого факта можно привести немало примеров.
Дефект в программном обеспечении бортовой системы космического корабля «Аполлона-8» уничтожил содержимое части памяти машины. За 10 дней полета «Аполлон-14» было обнаружено 18 дефектов. Серьезные дефекты в программном обеспечении не ограничивались только программой «Аполлон». Дефект в единственном операторе программы на Фортране (в операторе DO была пропущена запятая) привела к неудаче при первом запуске американского исследовательского корабля на Венеру. Дефекты в медицинском программном обеспечении явились причиной нескольких смертельных случаев, а дефект в программе проектирования самолета вызвал несколько серьезных авиакатастроф.
По мере введения АСОИУ во все сферы нашей жизни последствия недостаточной надежности становятся все серьезнее.
В невосстанавливаемых системах частотой отказов называется отношение числа отказавших элементов системы в единицу времени к числу элементов, первоначально установленных на испытания при условии, что отказавшие элементы не восстанавливаются и не заменяются исправными.
Так как число отказавших элементов в интервале времени Δ t может зависеть от расположения этого промежутка по оси времени, то частота отказов является функцией времени. Эта характеристика в дальнейшем обозначается a (t). Согласно определению
 , (3.1)
, (3.1)
где n (t) – число отказавших элементов в интервале времени от t – Δ t/ 2до t+ Δ t/ 2; Δ t – интервал времени; N 0 – число элементов системы, первоначально установленных на испытание.
Это выражение является статическим определением частоты отказов. Этой количественной характеристике надежности легко дать вероятностное определение. Вычислим в выражении (3.1) n (t), т.е. число элементов, отказавших в интервале Δ t. Очевидно,
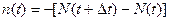 , (3.2)
, (3.2)
где N (t) – число элементов, исправно работающих к моменту времени t; N (t +D t) – число элементов, исправно работающих к моменту времени t+ Δ t/ 2.
При достаточно большом числе элементов N 0 справедливы соотношения
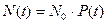 ,
,
 (3.3)
(3.3)
Подставляя (3.2) в (3.1) и учитывая (3.3)
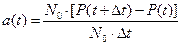 . (3.4)
. (3.4)
Устремляя Δ t к нулю и переходя к пределу,
 . (3.5)
. (3.5)
Из выражения видно, что частота отказов есть плотность распределения времени работы системы до ее отказа. Численно она равна взятой с противоположным знаком производной от вероятности безотказной работы.
Частота отказов, являясь плотностью распределения, наиболее плотно характеризует такое случайное явление, как время возникновения отказов. В этом ее основное достоинство как характеристики надежности.
Средней частотой отказов называется отношение числа отказавших элементов в единицу времени к числу испытываемых элементов при условии, что все элементы, вышедшие из строя, заменяются исправными (новыми или восстановленными). Таким образом,
 , (3.6)
, (3.6)
где n (t) – число отказавших элементов в интервале времени от t – Δ t/ 2до t+ Δ t/ 2; Δ t – интервал времени; N 0 – число испытываемых элементов (N 0 остается в процессе испытания постоянным, т.к. все отказавшие элементы заменяются исправными).
Сложная система состоит из большого числа элементов. Поэтому представляет интерес найти зависимость средней частоты отказов системы от средних частот отказов элементов. Для этой цели вводится понятие суммарной частоты отказов сложной системы.
Суммарной частотой отказов называется число отказов системы в единицу времени, приходящееся на одни ее экземпляр. Обозначим эту характеристику w c(t). Согласно определению, для одного элемента
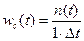 , (3.7)
, (3.7)
где n (t) – число отказавших элементов в интервале времени от t – Δ t/ 2до t+ Δ t/ 2; Δ t – интервал времени.
Если для определения w c(t) используется несколько элементов, то суммарная частота отказов вычисляется по формуле
 , (3.8)
, (3.8)
где ni (t) – число отказов i -го элемента в интервале времени от t – Δ t/ 2до t+ Δ t/ 2; Δ t – интервал времени;– число испытываемых элементов системы.
Отказы сложной системы состоят из отказов отдельных элементов, поэтому число отказов ni (t) системы в выражении (3.7) будет равно сумме всех отказов элементов. Если Ni – число элементов i -го типа, а wi – средняя частота отказов элементов i -го типа, то за промежуток времени (t, t+ Δ t) произойдет Ni × wi (t) × Δ t отказов элементов i -го типа, а всего отказов будет
 , (3.9)
, (3.9)
где r – число типов элементов.
Подставляя значение n (t) в (3.7) получится
 , (3.10)
, (3.10)
т.е. суммарная частота отказов сложной системы в момент времени t равна сумме средних частот отказов элементов.
Интенсивностью отказов называется отношение числа отказавших элементов системы в единицу времени к среднему числу элементов, исправно работающих в данный отрезок времени, при условии, что отказавшие элементы не восстанавливаются и не заменяются исправными.
Эта характеристика обозначается λ(t) и в ряде источников называется лямбда-характеристикой.
Согласно определению,
 , (3.11)
, (3.11)
где n (t) – число отказавших элементов в интервале времени от t – Δ t/ 2 до t+ Δ t/ 2; Δ t – интервал времени; Nср = (Ni + Ni+ 1 ) / 2 – среднее число исправно работающих элементов в конце интервала Δ t.
Для большинства элементов автоматизированных систем, в состав которых они входят, характерным свойством интенсивности отказов является свойство λ = сonstдля периода нормальной работы системы. Это объясняется отсутствием старения элементов на участке нормальной работы.
Выражение (3.11) является статическим определением интенсивности отказов. Для вероятностного преставления этой характеристики устанавливается зависимость между интенсивностью отказов, вероятностью безотказной работы и частотой отказов. Подставляя в выражение (3.11) вместо n (t) его значения из (3.2) и (3.3), получится
 . (3.12)
. (3.12)
Учитывая, что Nср = Ni - n (t)
 . (3.13)
. (3.13)
Устремляя Δ t к нулю и переходя к пределу,
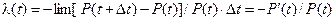 . (3.14)
. (3.14)
Δ t ®0
Интегрируя (3.14)
 . (3.15)
. (3.15)
Т.к. 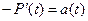 , то на основании (3.14)
, то на основании (3.14)
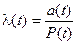 (3.16)
(3.16)
или
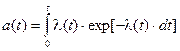 . (3.17)
. (3.17)
Выражения (3.15-17) устанавливают зависимость между вероятностью безотказной работы, частотой отказов и интенсивностью отказов. Выражение (3.16) является вероятностным определением интенсивности отказов.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 447; Нарушение авторских прав?; Мы поможем в написании вашей работы!