Отказы в восстанавливаемых системах

Надежность АСОИУ оценивают, в отличие от среднего времени безотказной работы, так называемой наработкой на отказ. Наработкой на отказ является среднее значение времени между соседними отказами при условии восстановления каждого отказавшего элемента.

Эта характеристика обозначается T о и определяется по формуле:

, (3.18)

где n – число отказов системы за время t; t_i – время исправной работы системы между (i – 1)-м и i- м отказами.

Из формулы (3.18) видно, что наработка на отказ является средним временем между соседними отказами. Этой формулой удобно пользоваться, если T о – характеристика лишь одного элемента системы. Для системы из нескольких элементов, T о _i вычисляется по формуле:

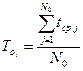, (3.19)

где t_срj – среднее время между соседними отказами j -го элемента, вычисляемое по формуле (3.18); N ₀ – число элементов.

Найти связь среднего времени между соседними отказами с другими количественными характеристиками надежности проще всего через среднюю частоту отказов. Действительно, если известны средние частоты отказов элементов сложной системы, то среднее число отказов системы в любом промежутке времени определяется ее суммарной частотой отказов. Тогда среднее время между соседними отказами будет равно величине, обратной суммарной частоте отказов, т.е.:

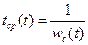, (3.20)

или

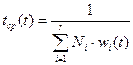, (3.21)

где r – число типов элементов.

Так как средняя частота отказов элементов w_i (t) при t ®¥ стремится к постоянной величине, равной 1/ T_i, то t_ср системы также стремится к постоянной величине, определенной выражением

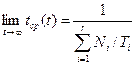, (3.22)

где T_i – среднее время безотказной работы системы из-за отказов элементов i- го типа.

Так как

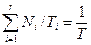, (3.23)

то при t ®¥ среднее время между соседними отказами стремится к ее среднему времени безотказной работы и в пределе равно Т, т.е.

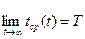. (3.24)

Среднее время между соседними отказами как всякое среднее значение случайной величины не может полностью характеризовать время безотказной работы системы.

Вероятность безотказной работы P (t), частота отказов a (t), средняя частота отказов w (t), интенсивность отказов λ(t)и наработка на отказ T ₀, среднее время между соседними отказами t_ср являются основными количественными характеристиками надежности. Каждая из них имеет свои достоинства и недостатки. Ни одна из них не является исчерпывающей характеристикой надежности. Только все они в совокупности во многих случаях могут характеризовать достаточно полно надежность системы в течение ее работы.

Дата добавления: 2014-01-07