Построение надежностно-функциональных схем

Надежностно-функциональные схемы (НФС) есть способ графического представления надежнос­тной структуры системы (состава используемых элементов, перечня выполняемых системой функций и взаимосвязи элементов в обеспечении работоспособности системы по каж­дой функции). Этот способ обеспечивает, с одной стороны, про­стоту и наглядность описания структуры системы, что очень важ­но на этапе рассмотрения ее с разработчиками, а с другой - строгую формальность и однозначность этого описания, необхо­димые при четкой постановке задачи анализа надежности.

НФС представляет собой граф, отображающий элементы системы и выполняемые ею функции и взаимосвязи между ними и позволяющий с помощью набора формальных правил для произвольной совокупности состояний (работоспособности или отказа) всех элементов однозначно определить состояние (работоспо­собность иди отказ) системы по каждой функции.

Граф является ориентированным однонап­равленным. Его узлами являются элементы рассматри­ваемой системы (прямоугольники) и выполняемые ею функции (ок­ружности); ребра (стрелки) отображают взаимодействие элементов в выполнении функции. В графе выделяются узлы высшего и низшего рангов: узел имеет высший (низший) ранг, если все связанные с ним ребра графа направлены только к нему (от него).

При рассмотрении НФС большую роль играет понятие пути. Путем в графе называют произвольную траекторию движения от од­ного узла к другому вдоль ориентированных ребер. Узел графа яв­ляется проходимым для путей, если соответствующий элемент си­стемы находится в состоянии работоспособности. Если элемент находится в состоянии отказа, то соответствующий узел закрыт для путей в графе. Узел имеет путь вверх, если существует хотя бы один путь, соединяющий его с одним из узлов высшего ранга.

При определенной совокупности состояний элементов система спо­собна выполнять некоторую функцию, если соответствующий этой функции узел графа имеет путь вверх» Если узел, отображающий данную функцию, не имеет пути вверх, то система не способна к ее выполнению.

Этих не сложных правил достаточно, чтобы на основе НФС для произвольного набора состояний элементов системы однозначно определить, работоспособна или неработоспособна рассматриваемая система по каждой из ее функций.

Простота и наглядность, а также строгая формальность и однозначность НФС является унифици­рованным способом описания системы - при постановке задачи анализа их надеж­ности.

Рассмотрим примеры НФС некоторых типовых надежностных структур комплекса технических средств системы.

Независимое соединение элементов. Система включает n элементов, каждый из которых выполняет свою функцию независимо от работы других элементов. Таким образом, всего система выполняет n функций: Ф ₁, Ф ₂ ,...,Ф_n. НФС такой системы содержит n узлов высшего ранга, соответствующих элементам, и а узлов низшего ранга, соответствующих функциям. Узлы высшего и низшего рангов связаны попарно (рис. 4.1).

Рис. 4.1 Рис. 4.2

Последовательное соединение элементов. На НФС все последовательные соединения элементов выстраивается в одну цепь узлов с одинаковым направлением стрелок. Очередность элементов в цепи безразлична; безразлично также, какому из элементов соответствует узел высшего ранга; (n +1)- m в указанной цепи включается реализуемая системой функция (рис. 4.2).

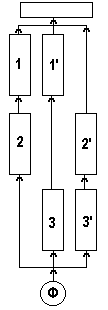
Параллельное соединение элементов. НФС представленна на рис. 4.3.

В тех случаях, когда рассматриваемая структура не входит в состав более сложной системы и функционирует самостоятельно, в граф удобно ввести один дополнительный (n +1)-й узел высшего ранга. Если принять, что этот узел обладает абсолютной надежностью, то введение его, очевидно, не повлияет на надежность системы.

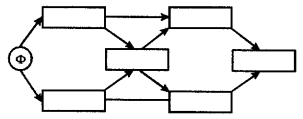Рис. 4.3 Рис. 4.4 Рис. 4.5 Рис. 4.6

Двухфункциональная система. Система включает два элемента и выполняет две функции. Причем в выполнении одной из них участвуют оба элемента, а другой - только один. Эта система отображается графом (рис. 4.4), в котором одному элементу I соответствуют два узла: I' и I'', причем только один из них I'' имеет высший ранг. При анализе надежности такой системы следует иметь в виду, что узлы, соответствующие одному и тому же элементу, имеют одинаковые не только распределения случайных величин, но и их реализации.

Мажоритарная структура «2 из 3». Трехэлементная система, выполняющая одну функцию и сохраняющая работоспособность при работоспособности любых двух ее элементов. Введение дополнительных узлов позволяет просто отобразить эту структуру (рис. 4.5). Аналогично отображаются любые мажоритарные структуры.

Мостиковые соединения легко описываются НФС. Однофункциональная мостиковая схема приведена на рис. 4.6

Дата добавления: 2014-01-07