Инженерная методика вычисления показателей надежности

Исходными данными для оценки надежности l-методом являются:

- надежностно-функциональная схема (НФС) или схема расчета надежности со словесным описанием;

- интенсивности отказов элементов системы l _i (t)= l i =const, Для систем с техническим обслуживанием, проводимым через фиксированные интервалы времени t, вместо l _i берется среднее значение функции l _i (t) на интервале t.

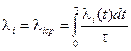(4.7)

Расчет надежности системы проводится в следующей последовательности:

- построение упрощенного варианта НФС из основных элементов системы (для систем с произвольной структурой);

- вычисление интенсивностей отказов системыL ;

- вычисление вероятности безотказной работы за период времени t -P (t);

- вычисление средней наработки до отказа Т ₁.

Построение упрощенного варианта НФС из основных элементов системы осуществляется следующим образом.

Из НФС более сложной структуры, чем основное соединение элементов, выбираются только основные (рабочие) элементы и они соединяются последовательно. Например, из резервированной группы элементов с целой кратностью резервирования выбирает только один рабочий элемент, из группы элементов с дробной кратностью резервирования (m ₁= m / k) - k рабочих элементов.

Интенсивность отказов системы определяется следующим образом:

, (4.8)

где n - число основных элементов системы, l _i - интенсивность отказов i-го элемента.

Если система имеет группы равнонадежных элементов, то формулу (4.8) можно записать в виде:

, (4.9)

где z -количество групп равнонадежных элементов; n_j -количество элементов в j -й группе; l _j - интенсивность отказов элементов в j -й группе.

Вероятность безотказной работы системы завремя t определяется по формуле:

(4.10)

Для вычисления значений P (t) можно использовать таблицу значений функции e^-x.

В случае, когда L t £0,1, для упрощения расчетов надежности рекомендуется пользоваться следующей приближенной формулой:

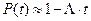(4.11)

Средняя наработка до отказа Т ₀ определяется следующим образом:

. (4.12)

Примеры

Пример 1. Пусть дана невосстанавливаемая система, НФС которой приведена на рис. 4.1. Закон распределения времени безотказной работы элементов - экспоненциальный. Интенсивность отказов элементов приведена в табл. 4.1.

Таблица 4.1

Номер группы элементов	Количество элементов	Интенсивность отказов l i,1/ч
		0,3×10^-5
		0,5×10^-5
		0,14×10^-5
		0,05×10^-5
		0,3×10^-5
		0,2×10^-5
		0,1×10^-5
		0,05×10^-5

Требуется определить вероятность безотказной работы системы за 250 часов и среднюю наработку до отказа.

Вычисление интенсивности отказов системы. Подставляем в формулу (4.9) значения интенсивностей отказов элементов:

L=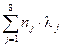=(14×0,3+4×0,5+56×0,14+168×0,05+1×0,3+2×0,2+6×0,1+3×0,05)×10^-5=23,89×10^-5 (1/ч).

Вычисление безотказной работы системы за 250 часов находим по формуле

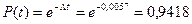. (4.10)

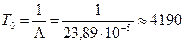ч. (4.11)

Пример 2. Проектируется однофункциональная восстанавливаемая система (рис. 4.8). Группа элементов 1 - резервирование с целой кратностью; группа элементов 2 - ненагруженный резерв; группа элементов 5 - резервирование с дробной кратностью, нагруженный резерв; группа элементов 6-общее резервирование, нагруженный резерв. Закон распределения времени безотказной работы экспоненциальный. Интенсивности отказов элементов приведены в табл.4.2.

Таблица 4.2

Номер элемента	Интенсивность отказов элемента l i, 1/ч
	0,5 ×10^-5
	0,5 ×10^-5
	0,5 ×10^-5
	0,5 ×10^-5
	0,2 ×10^-5
	0,2 ×10^-5
	0,1 ×10^-5
	0,1 ×10^-5
	0,3 ×10^-5
	0,3 ×10^-5
	0,3 ×10^-5
	0,4 ×10^-5
	0,4 ×10^-5
	0,45 ×10^-5
	0,45 ×10^-5

Требуется определить приближенное значение вероятности безотказной работы системы за 1000 часов и среднюю наработку до отказа.

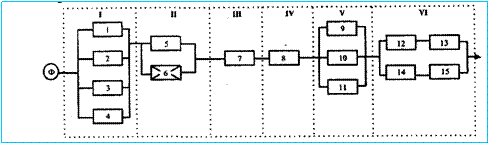
Рис. 4.8

Построение упрощенного варианта НФС из основных элементов системы.

Из НФС системы следует выбрать только основные (рабочие) элементы:

- из группы 1 с целой кратностью резервирования - элемент 1;

- из группы 2 - элемент 5;

- элемент 7;

- элемент 8;

- из группы 5 с дробной кратностью резервирования (m =1/2) - элементы 9 и 10;

- из группы 6 - элементы 12 и 13.

Последовательная цепь этих элементов - вариант НФС, по которому производится расчет надежности.

Вычисление интенсивности отказов системы. По формуле (4.8) находим

L=l₁+l₂+l₇+l₈+l₉+l₁₀+l₁₂+l₁₃= (0,5+0,2+0,1+0,1+0,3+0,3+0,4+0,4)×10^-5=2,3×10^-5 1/ч.

Вычисление безотказной работы системы за 1000 часов. Подставляем значения Lи t в (4.10)

.

Вычисление средней наработки до отказа. По формуле (4.12) находим

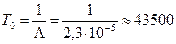ч.

Пример 3. Дана схема, НФС которой - основное соединение четырех элементов. Система с техническим обслуживанием, проводимым через каждые 20 часов. Данные по надежности элементов - в табл. 4.3.

Таблица 4.3

Номер элемента	Закон распределения	Параметр распределения
	Релея
	Релея
	Релея
	Релея

Требуется определить приближенное значение вероятности безотказной работы системы за 2000 часов.

Определение средних значений интенсивностей отказов элементов. Для закона распределения Релея функция l _i (t) записывается следующим образом:

. (4.11)

Подставляя формулу (4.11) формулу (4.7) найдем выражение для среднего значения интенсивности отказов i -го элемента:

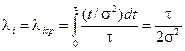. (4.12)

При подстановке значений t и s _i, в полученное выражение найдем l _iср для каждого элемента:

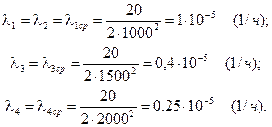(4.13)

Вычисление интенсивности отказов системы. По формуле (4.8) находим

L=2l₁+l₃+l₄= (2×1+0,4+0,25)×10^-5=2,65×10^-5 1/ ч.

Вычисление вероятности безотказной работы системы. Подставляя в (4.10) значения L и t, получим

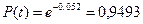. (4.14)

Пример 4. Дана невосстанавливаемая система. НФС - основное соединение элементов. Закон распределения времени безотказной работы элементов - экспоненциальный. Значения интенсивностей отказов системы приведены в табл. 4.4.

Таблица 4.4

Номер элемента	Интенсивность отказов элемента l i, 1/ч
	0,1 ×10^-5
	0,4 ×10^-5
	0,15 ×10^-5
	0,20 ×10^-5
	0,20 ×10^-5
	0,25 ×10^-5
	0,10 ×10^-5

Требуется определить время безотказной работы системы за 1000 часов.

Вычисление интенсивности отказов системы. По формуле (4.8) определяем

L=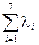=(0,1+0,4+0,15+0,20+0,20+0,25+0,1)×10^-5=1,40×10^-5 (1/ч). (4.15)

Вычисление вероятности безотказной работы системы за 1000 часов. В связи с тем, что:

L×t =1,4×10^-5 × 1000=0,014<0,1, (4.16)

для расчета можно воспользоваться формулой (4.11):

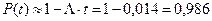. (4.17)

Дата добавления: 2014-01-07