Примеры расчета показателей надежности методом марковских процессов

Пример 1. Требуется вычислить характеристики и показатели надежности системы, НФС которой представлена на рис. 4.9.

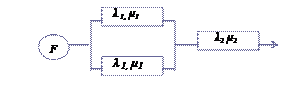Рис. 4.9

Представление исходных данных. Отказ системы наступает в том случае, если откажут оба элемента, входящие в дублированную пару, или произойдет отказ элемента № 2.

Элементы дублированной пары равнонадежны с интенсивностью отказов l₁=0,02 1/час и интенсивностью восстановлений m₁=1 1/час. Интенсивности отказов и восстановлений нерезервированного элемента № 2 равны соответственно l₁=0,01 1/час и m₁=1 1/час. Обслуживает систему одна ремонтная бригада, приоритет обслуживания - прямой, то есть восстановление отказавших элементов осуществляется в порядке их отказов. В начале функционирования все три элемента находятся в исправном состоянии. Время непрерывной работы системы t= 10 час.

Построение графа состояний. Граф состояний изображен на рис. 4.10.

Рис. 4.10

Узлам графа приписаны следующие состояния: «0» - все элементы исправны, «1» - один из элементов дублированной пары отказал и восстанавливается, остальные элементы исправны, «2» элемент № 2 отказал и восстанавливается, остальные элементы исправны, «3» - оба элемента дублированной пары отказали, первый отказавший элемент находится в ремонте, второй находится в очереди на обслуживание, «4» - в отказе находится элемент № 2 и один из элементов дублированной пары. При этом первым обслуживается элемент дублированной пары. Ветвям приписаны интенсивности переходов, равные интенсивностям отказов и восстановлений тех элементов, из-за которых происходят указанные переходы. Состояния «2», «3», «4» являются отказовыми и отмечены на графе крестами. Для определения P (t) в графе поставлены экраны в виде пунктирных линий.

Составление системы дифференциальных уравнений. Система дифференциальных уравнений для определения P (t) имеет вид:

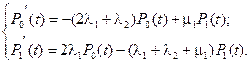(4.53)

Определение вероятностей состояний системы. Вычислим вероятности исправных состояний P ₀(t) и P ₁(t) при условии, что все элементы при t= 0 исправны, то есть P ₀(0)=1, P ₁(t)=0. В преобразованиях Лапласа система уравнений имеет вид:

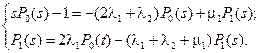(4.54)

Решая эту систему алгебраических уравнений, получим:

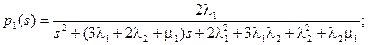(4.55)

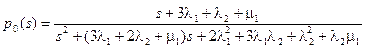. (4.56)

Определение вероятности безотказной работы. Вероятность безотказной работы в преобразованиях Лапласа будет иметь вид:

. (4.57)

Подставляя числовые значения интенсивностей, получим

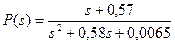. (4.59)

Переходя от изображения к оригиналу, получим вероятность безотказной работы системы, как функцию времени

P(t)= 1,002 e ^{-0,011 t} - 0.002 e^-0,569t. (4.59)

Определение средней наработки до отказа. На основании формулы и в соответствии с выражением для P(s), подставив вместо s значение 0, получим T ₀ = 87,69 час.

Определение функции готовности. Для определения функции готовности уберем экраны из графа состояний. Тогда система дифференциальных уравнений будет иметь вид:

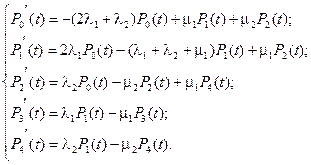(4.60)

Так как по условию задачи при t= 0 все элементы исправны, то P ₀(0)=1, P ₁(0)= P ₂(0)= P ₃(0)= P ₄(0)=0. Из графа состояний видно, что число исправных состояний меньше числа отказовых, поэтому К _г(t) будем вычислять по формуле, указанной выше. Запишем систему уравнений в преобразованиях Лапласа:

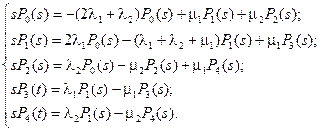(4.61)

Решая эту систему при заданных значениях интенсивностей переходов, получим

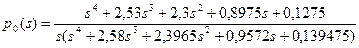; (4.62)

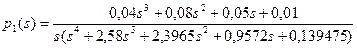. (4.63)

Найдем изображение функции готовности:

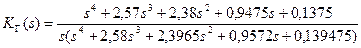. (4.64)

Чтобы перейти от изображения К_г(s) к оригиналу К_г(t), одним из известных методов найдем корни знаменателя: s₁ = 0; s₂= -0,436; s ₃= -0,5; s ₄= -0,632; s ₅= -1,012. Тогда оригинал имеет вид:

K _г(t) = 0,986+0,017e^{-0436 t} -0,014e^{-0,632 t} +0,011e^{-1,012 t}. (4.65)

Для t =10 час., K _г(10)=0,986.

Определение коэффициента готовности. Принимая во внимание выражения для K _г (t) или K _г(s), определяем коэффициент готовности K _г(10)=0,986.

Определение наработки на отказ. Наработку на отказ найдем по известным финальным (предельным) вероятностям состояний, полученным из выражений для p ₀(s) и p ₁(s) соответственно.

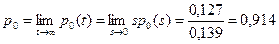, (4.66)

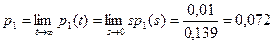. (4.66)

Определение среднего времени восстановления. Среднее время восстановления вычисляется следующим образом:

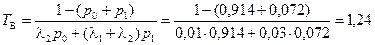. (4.68)

Поскольку коэффициент готовности, наработка на отказ и среднее время восстановления связаны между собой соотношением

, (4.69)

то это равенство может служить проверкой правильности расчетов.

Пример 2. Вычислить коэффициент готовности, наработку на отказ и среднее время восстановления системы, НФС которой изображена на рис. 4.11.

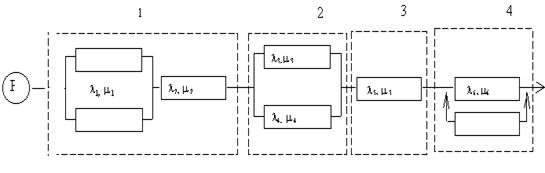Рис. 4.11

Схема представляет собой основное соединение четырех независимых типовых структур, обладающих следующими данными:

- типовая структура №1: l₁=0,02 1/час; m₁=0,5 1/час; l₂=0,01 1/час; m₂=1 1/час, одна ремонтная бригада, прямой приоритет обслуживания;

- типовая структура № 2: l₃=0,03 1/час; m₃=0,6 1/час; l₄=0,04 1/час; m₄=0,8 1/час, одна ремонтная бригада, обратный приоритет обслуживания;

- типовая структура № 3: l₅=0,01 1/час; m₅=1 1/час, одна ремонтная бригада;

- типовая структура № 4: l₆=0,02 1/час; m₆=0,2 1/час, одна ремонтная бригада, прямой приоритет.

Определение характеристик К _{г i} , T_i, P_oi для каждой типовой структуры системы. Как следует из примера, требуемые характеристики для типовой структуры № 1 имеют следующие значения: К _{г i} =0,986, T_i,=87,26 час =0,982.Для других структур эти характеристики вычисляются аналогично.

Результаты расчетов представлены в табл. 4.6.

Таблица 4.6

Дата добавления: 2014-01-07