Основные задачи установления закона распределения

В процессе эксплуатации информационных систем в эксплуатационном журнале регистрируются данные о продолжительности интервалов безотказной (и бессбойной) работ системы в це­лом и отдельных устройств моментах возникновения отказов (с указанием отказавше­го устройства и причины отказа), моментов появления сбоев (с указанием узла, обнаруже­ны сбои), продолжительности работ по устранению отказов и работ по восстановле­нию достоверности информации после сбоев, о времени проведения, продолжительности и результатах профилактических испытаний и другие данные о работе ТС.

Эти данные могут быть использованы для определения количественных значений основ­ных надежностных характеристик. Вместе с тем эти данные позволяют получать законы распределения времени между отказами, времени восстановления и других случай­ных величин, т.е. практически строить экспериментальные модели надежности машины. ТС.

Эти модели могут быть положены в основу расчетов и имитационного моделирова­ния надежности соответствующих ТС. Зафиксированные в журнале длительности интервалов нормальной работы между отка­зами или продолжительности работ по восстановлении можно рассматривать как неко­торую выборку из всего множества значений, которые принимает данная случайная ве­личина (выборку конечного объема из генеральной совокупности данной случайной ве­личины).

Пусть Х_i, Х ₂, X_i ,..., Х_n - независимые измерения исследуемой случайной величины, причем X_i называется выборочным значением X -каналов, а N - объемом выборки.

Рассмотрим, каким образом, обрабатывая результаты наблюдений можно установить, какому теоретическому закону распределения подчиняется исследуемая случайная вели­чина.

Выделим три основные задачи, которые следует последовательно решить. Первая задача - это задача об определении числовых характеристик случайной величины математического ожидания, дисперсии (среднего квадратичного отклонения), асимметрии, эксцесса и т.п.; другими словами, это задача определения по выборке объе­мом N выборочных начальных и центральных моментов случайной величины.

Вторая задача состоит в определении соответствующего теоретического распреде­ления. Это - задача сглаживания или выравнивания статистических данных.

На основании выборочных значений случайной величины, сгруппированных, спе­циальным образом, выдвигается гипотеза о том, что исследуемые случайные величины - наработка на отказ Т ₀, время восстановления Т _В и т.д. могут быть описаны тем или иным теоретическим распределением. При этом чаще всего параметры теоретического распределения определяются также по самой выборке, например, исходя из того, что моменты теоретического распределения должны быть равны выборочным моментам (метод моментов).

Как правило, гипотеза о теоретическом распределении выдвигается на основании опыта исследователя; очевидно, что возможно выдвижение и неверной гипотезы.

Третья задача состоит в проверке гипотезы (правдоподобия гипотезы). Она реша­ется путем вычисления специальных статистик - величин, характеризующих степень рас­хождения между опытными данными и теоретическим распределением. Статистика формируется таким образом, что заранее известно ее распределение; это позволяет определить вероятность того, что выборка может быть описана принятым теоретиче­ским распределением.

Кроме перечисленных задач могут возникнуть и другие, например задача об опреде­лении объема выборки для получения достоверных оценок и т.д.

Первая из перечисленных задач решается достаточно просто при использо­вании ЭВМ.

Статистические оценки моментов получают как значения определенных функций от вы­борочных значений случайной величины. В частности, статистическая оценка r -го мо­мента (начального или центрального) может быть принята равной выборочному r -му моменту (начальному или центральному). Последние вычисляются по формулам:

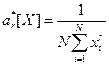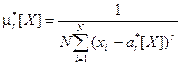; , (6.1)

где a_r*, μ_r* - соответственно начальный и центральный моменты r -го порядка. Очевид­но, что статистически оценки моментов являются случайными величинами.

Первый начальный момент - это выборочное среднее для его обозначения часто при­меняется символ` X.

Если выборочное среднее значение` X вычисляется по выборке объемом N, то среднее квадратичное отклонение случайной величины` X от математического ожидания М [` X ] равно:

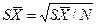. (6.2)

Можно показать, что` X имеет нормальное распределение; это позволяет решить задачу об определении объема выборки.

Дата добавления: 2014-01-07