Оценка надёжности оператора

Необходимость разработки методов, оценки надёжности оператора и системы в целом, настоятельно диктуется потребностями практики. Наличие количественных оценок позволяет придать объективный характер решению вопросов, которые возникают в процессе проектирования, изготовления и эксплуатации системы.

Американские учёные У. Вудсон и Д. Коновер считают, что количественное выражение надёжности оператора является чрезвычайно трудной задачей. Б.Ф. Ломов считает, что «вряд ли мы когда-либо получим для человека некоторый абсолютный коэффициент надёжности, который окажется справедливым для всех условий». Это, однако, не отвергает единой системы принципов и методов определения надёжности работы оператора.

Анализ зарубежных исследований, посвящённых качественным и количественным методам оценки и прогнозирования надёжности человека-оператора, привел Д. Мейстер. Он называет 22 метода, которые удалось найти в психологической и технической литературе по проблеме надёжности. Проиллюстрируем содержание некоторых из них, включенных по классификации Мейстера в группу аналитических методов.

Метод AIR DATA (1962) разработан Американским институтом исследований. В основе его лежит «банк данных» по временным и надёжностным характеристикам выполнения человеком отдельных операций, которые могут входить в структуру его деятельности в системе. Метод преследует следующие цели:

- прогнозирование надёжности деятельности оператора;

- выявление ошибок, допущенных на стадии проектирования;

- выдача предложений по отбору и обучению операторов.

Данные собраны на основании 164 лабораторных психологических экспериментов (Мейстер, 1970) и приведены в виде вероятностей безошибочного выполнения отдельных операций, минимально необходимого времени для их совершения, а также в виде временных поправок, обусловленных индивидуальными характеристиками человека.

Техника использования метода сводится к определению надёжности выполнения задачи путём последовательного перемножения вероятностей безошибочного выполнения входящих в него отдельных операций и расчёта суммарного времени выполнения задания по временным затратам на отдельные операции. Метод применим для задач дискретного типа и основан на предположении независимости входящих в структуру задания операций.

Метод THERP (1963) получил наибольшее распространение. Согласно этому методу анализ систем проводится с помощью построения вероятностного дерева, каждой ветви которого приписывается соответствующая вероятность её реализации. Вероятностное дерево для всей системы становится исключительно сложным и труднообозримым, поэтому метод применяется обычно на уровне подсистемы приблизительно для 50 ветвей и при условии довольно четкого понимания связей в системе. Исходные надежностные характеристики могут браться из «банка данных», а сами расчеты проводятся с помощью ЭВМ. Пример аналитического расчета с применением данного метода рассмотрен Д. Мейстером и Дж. Рабидо (1970), а последовательность этапов работы по нему раскрывается М. Монмолленом (1973). В принципе, метод позволяет учитывать как независимые, так и зависимые друг от друга операции.

В.Аскрен и Т.Регулинский (1967) считают возможным применение классических методов теории надежности для определения характеристик надежности оператора. Они экспериментальным путем нашли закон распределения ошибок оператора как функцию от времени.

Мейстер отмечает, что количественные методы продолжают уточняться и совершенствоваться, а некоторые из них уже сейчас дают обнадеживающие результаты. Однако в целом, по его мнению, к ним есть существенные замечания. Прежде всего, это касается отсутствия проверки валидности методов, в большинстве случаев присутствует элемент субъективизма.

Эволюцию взглядов и идей в отечественной инженерной психологии относительно количественных методов оценки надежности оператора можно проследить по работам в этом направлении (Губинский, Лобов, Мансуров, Суходольский, 1967; Николаев, 1970). В ряде работ приводятся систематизированные обзоры существующих количественных методов (Фокин, 1971; Ронжин, 1972; Зараковский, Королев, Медведев, Шлоен, 1974).

Среди известных методов выделяются обобщенно-структурный метод (ОСМ) А.И. Губинского и системный метод Ю.Г. Фокина, как наиболее полно обеспеченные математическими моделями и методиками для практического применения. В математических моделях ОСМ предусмотрена принципиальная возможность учёта самоконтроля оператора. Согласно принципу иерархического структурирования как одному из методических принципов ОСМ анализ конкретной деятельности оператора осуществляется как бы «сверху вниз» с представлением её в виде структур на уровне совокупности решаемых задач (это высший уровень структурирования деятельности), затем на уровнях отдельной задачи, отдельного алгоритма, блока операций и, наконец, отдельной операции. При этом на каждом из перечисленных уровней рассмотрения применимы одни и те же критерии оценки: надёжность выполнения структуры и временные запреты на её выполнение.

Количественная же оценка деятельности оператора осуществляется в обратной последовательности, т.е. «снизу вверх», и поэтому уровень отдельных операций является тем исходным уровнем, на котором необходимо располагать соответствующими надёжностными показателями.

Численные значения выбранных критериев надёжности оператора (вероятность безошибочного выполнения отдельных операций и временные затраты на их осуществление) могут определяться либо на основании уже известных экспериментально-психологических данных, приведённых в литературе, либо путём проведения специальных испытаний на пульте управления или его макете. Усреднённые временные и надёжностные показатели могут быть получены из эксперимента, поставленного на представительной выборке из соответствующей совокупности испытуемых.

Исходные надёжностные данные получаются в специально организованных для этой цели экспериментах. Практика психологических исследований повседневно обогащается обширным эмпирическим материалом, получаемым при изучении специальных задач. Однако, замечает Г.В. Суходольский, в этих экспериментах, к сожалению, не всегда используются общепринятые количественные меры. В итоге это приводит к утрате количественных данных, характеризующих психологические аспекты деятельности оператора, которые могли бы найти полезное применение при решении различных задач в области теории и практики проблемы надёжности оператора.

При оценке надёжности оператора специалисты предлагают учитывать следующие факторы:

долговременная выносливость - сохранение человеком работоспособности на заданном уровне в течение определённого времени; с нарастанием утомления надёжность снижается за счет увеличения неточностей, ошибок; снижения внимания;

устойчивость к воздействию факторов среды: температуры, влажности, давления, шума, ускорения, связанная с состоянием нервной системы оператора;

работоспособность в экстремальных условиях, т.е. способность принимать правильные решения при дефиците времени, в аварийных ситуациях;

помехоустойчивость - работоспособность оператора в условиях шумов, посторонней речи, движения посторонних предметов в поле зрения, помехоустойчивость оператора повышается за счёт приобретения опыта работы, тренировок, улучшения условий труда;

спонтанная отвлекаемость - отвлечение внимания в результате внутренних спонтанных колебаний внимания, в первую очередь, при длительном пассивном наблюдении;

переключаемость - время «вхождения» в новую деятельность (при этом стереотипные решения предшествующих задач могут переноситься на вновь решаемые), определяется индивидуальными особенностями каждого человека.

В ряде случаев оператор повышает надёжность системы, что объясняется, например, его способностью восстанавливать сигналы на фоне шумов и своевременно парировать отказы элементов ТС системы.

Надёжность оператора характеризуется: безошибочностью, готовностью, восстанавливаемостью и своевременностью. Основным показателем безошибочности является вероятность безошибочной работы, которую можно вычислять как на уровне отдельной операции, так и на уровне алгоритма в целом. Для типовых, часто повторяющихся операций в качестве показателя безошибочности можно использовать также интенсивность ошибок. Этот показатель определяют, как правило, в расчёте на одну выполненную операцию (алгоритм). По статистическим данным применительно к фазе устойчивой работоспособности (рис. 8.1.):

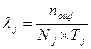
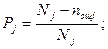
(8.1)

где P_j - вероятность безошибочного выполнения операций j- го вида; l _j - интенсивность ошибок, допущенных при выполнении операций j -го вида; N_j, n_ошj - общее число операций j -го вида и допущенное при этом число ошибок; T_j - среднее время выполнения операции j -го вида.

Зная интенсивность ошибок l_j при выполнении различных операций и алгоритм работы оператора, можно 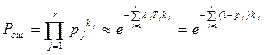найти вероятность безошибочного выполнения этого алгоритма.

(8.2)

где k_j – число выполненных операций j -го типа; r – число различных видов операций (j= 1,2 ,…,r).

Важным показателем надёжности является коэффициент готовности, представляющий собой вероятность включения человека-оператора в работу в любой произвольный момент времени определяемой выражением:

, (8.3.)

где T¢ – время, в течение которого человек-оператор по тем или иным причинам не может принять поступившую к нему информацию; T¢¢ – общее время работы оператора.

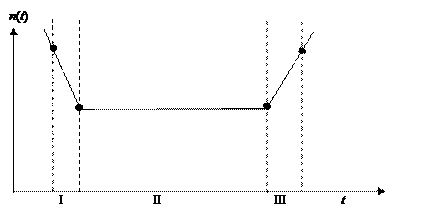
I – фаза врабатываемости; II – фаза устойчивой работоспособности; III – фаза утомления.

Рис. 8.1. Изменение надежности оператора на протяжении рабочей смены

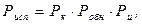В качестве показателя восстанавливаемости используют вероятность исправления оператором допущенной ошибки:

(8.4.)

где P_к – вероятность выдачи сигнала схемой контроля; P_обн – вероятность обнаружения оператором сигнала контроля; P_и – вероятность исправления ошибочных действий при повторном выполнении алгоритма.

Этот показатель позволяет оценить возможность самоконтроля оператором своих действий и исправления допущенных им ошибок.

Показателем своевременности является вероятность выполнения задачи в течение времени t £ t_e, где t_e – лимит времени, превышение которого рассматривается как ошибка. Эта вероятность определяется формулой:

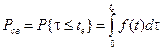, (8.5.)

где f (t) – функция распределения времени решения задачи оператором.

Время t_e может быть как постоянной, так и случайной величиной. В первом случае вероятность P_св определяется выражением, записанным выше. Во втором случае вычисление P_св довольно сложно. Оно упрощается, если t и t подчинены нормальному распределению с параметрами `t, dt и ` t_e, d t_e соответственно (рис. 8.2).

Надёжность деятельности оператора не остаётся величиной постоянной, а меняется с течением времени. Это изменение обусловлено как изменением условий деятельности, так и колебаниями состояния оператора. Поэтому при определении его надёжности в каждом конкретном случае выбираются те или иные факторы, наиболее характерные для данного вида деятельности. С каждым из этих факторов связывается определённое состояние системы, и для каждого из этих состояний находится конкретное значение изучаемого показателя надёжности оператора.

На рис. 8.2. показано изменение состояний системы во времени.

Законы распределения F (t) – времени решения задачи человеком-оператором, F (t_e) – лимита времени.

Рис. 8.2. Законы распределения

Среднее значение вероятности безошибочной работы оператора (при условии независимости появления ошибок).

(8.6)

где P_i – вероятность наступления _i -го состояния системы; P_оп /i – условная вероятность безошибочной работы оператора в i -м состоянии; m – число рассматриваемых состояний системы.

Вероятность P_i в ряде случаев могут быть определены методами теории массового обслуживания. Вероятность P_оп/i может быть получена в результате анализа деятельности оператора по формуле (8.2) или экспериментально.

Дата добавления: 2014-01-07