Кривые Безье

Сегмент кривой Безье (Bezier) третьего порядка описывается положе­нием четырех точек. Две из них являются опорными (узлами кривой): начальная точка Р₀ (х₀, у₀) и конечная точка Р₃ (х₃, у₃). Точки Р₁ (x_l y) и Р₂ (х₂, у₂), определяющие положение касательных относительно от­резка, называют управляющими (1). Метод построения кривой Безье основан на использовании пары касательных (управляющих линий), проведенных к сегменту кривой в его окончаниях. На форму кривой влияют угол наклона касательной и длина ее отрезка (рис. 255).

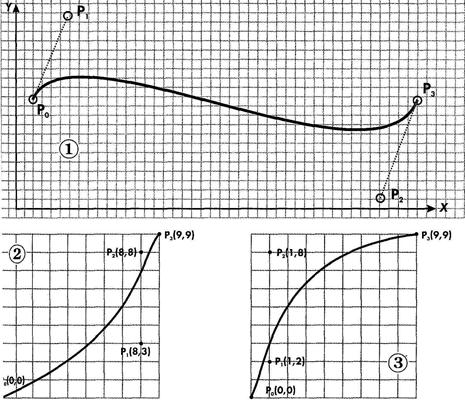
Параметрическое уравнение Безье описывает положение точек и, тем самым, форму кривой. Уравнение решают относительно параметра t, принимающего значения от 0 (в начальной точке) до 1 (в конечной точ­ке). При построении сегмента кривой Безье на плоскости рассчитыва­ют координаты x и у (для четырех точек, из них двух управляющих):

R(t) = Р₀(1 - t)³ + Р₁t(1 - t)2 + P₂t²(l - 1) + P₃t³, где 0 < t <1;

Значение t определяет степень влияния точек на форму кривой (2, 3). Например, при t = 0,333 наибольший «вес» приобретает точка P₁ (x_v y), а при t = 0,666 — точка Р₂ (х₂, у₂). Из приведенных уравнений вытека­ет, что кривая может проходить лишь через начальную и конечную опорные точки сегмента (Р₀, Р₃). Тем самым достигаются простота опи­сания и стабильность кривой Безье.

Свойство кривой Безье

Кривые Безье обладают рядом свойств, определяющих возможность их использования в векторной графике. С геометрической точки зре­ния, производной кривой Безье будет другая кривая Безье, векторы управляющих точек которой определяются вычислением разностей векторов управляющих точек исходной кривой.

Основные свойства кривой Безье:

ü непрерывность заполнения сегмента между начальной и конечной точками;

ü кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки (1);

ü при наличии только двух контрольных точек сегмент представляет собой прямую линию (2);

ü прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек (2);

ü 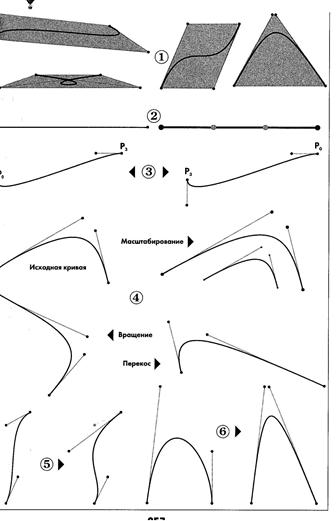кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой (3);

ü масштабирование и изменение пропорций кривой Безье не нарушает ее стабильности, так как она с математической точки зрения «аффинно инвариантна» (4);

ü изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье (5);

ü степень кривой всегда на одну ступень ниже числа контрольных точек. То есть при трех контрольных точках форма кривой — парабола;

ü размещение дополнительных контрольных точек вблизи одной позиции увеличивает ее «вес» и приводит к приближению траектории кривой к данной позиции (6);

ü окружность не может быть описана параметрическим уравнением кривой Безье;

ü невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые).

ü

ü

ü Метод кунса

ü По данному методу на участке от i-той точки принятой за начальную t= (0) до i+1-конечной t= (1) происходит плавный переход от одних параметров (например дуги окружности по предыдущим точкам до i- ой точки) к параметрам i+1 и далее.

Функции перехода:

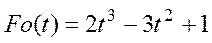
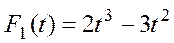
Дата добавления: 2014-01-07