Методы оптимизации среднего остатка денежных активов

Оптимальным остатком денежных активов считается тот минимум денежных средств, который необходим для расходования в предстоящем году по планируемым операциям.

Формула его расчета следующая:

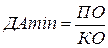, (2.23)

где 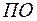- платежный оборот, денежные активы в планируемом году (данные берутся из плана доходов и расходов денежных средств).

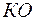- коэффициент оборачиваемости денежных активов (в количествах раз) в аналогичном по сроку отчетном периоде.

или

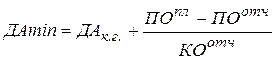, (2.24)

где 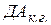- остаток денежных средств на конец года;

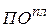и 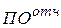- платежи в предстоящем и отчетном периодах.

В практике зарубежного финансового менеджмента при оптимизации остатка денежных активов используются наиболее сложные методики, например, модель Баумоля.

В соответствии с этой моделью рассчитывают остатки денежных средств на предстоящий период в следующих размерах:

а) min

б) opt (он же максимальный)

в) средний

Min денежного остатка принимается равным 0.

Opt (max) рассчитывается по формуле:

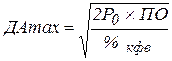, (2.25)

где 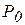- средняя сумма расхода по обслуживанию одной операции с краткосрочными финансовыми вложениями;

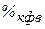- ставка по краткосрочным финансовым вложениям в рассматриваемом периоде (в виде десятичной дроби).

Эта модель применяется в случаях, если:

- платежный оборот в течение года постоянен;

- все денежные резервы хранятся в виде краткосрочных финансовых вложений;

- min остаток денежных активов равен 0.

Предполагается что, как только остаток денежных активов достигнет min, т.е. = 0, его пополнение происходит за счет краткосрочных финансовых вложений или краткосрочных кредитов банка. Чем меньше размер среднего и max остатка денежных активов тем чаще возникает необходимость в пополнении этого остатка, а значит тем больше будут расходы, связанные с получением кредита или с продажей краткосрочных активов. Таким образом, размер расходов пропорционален частоте пополнения денежных остатков. Этот вид расходов обозначен «».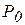

Для экономии общей суммы 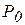следует увеличить период (или снизить частоту) этого пополнения. Но в этом случае возрастают величины «opt» и «max» остатков денежных активов, что также нежелательно, поскольку теряется выгода от альтернативных вариантов вложения денег в форме краткосрочных финансовых вложений.

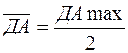, (2.26)

где 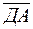- средний остаток денежных активов.

В отечественной практике еще сложно использовать ту модель и другие, подобные ей (например, модель Миллера – Орра) из-за:

- хронической нехватки оборотных средств (невозможно сформировать остаток денежных активов в необходимых размерах с учетом их резерва);

- трудности планирования платежного оборота (из-за несвоевременных денежных поступлений).

Тем не менее, разработаны формы оперативного регулирования среднего денежного остатка.

Дата добавления: 2014-01-07