Преобразование сигнала в частотной области

Очевидно преобразование входного случайного сигнала линейной системой в частотной области (Рис. 5.20.) связано со спектральной и взаимной спектральной плотностями.

Рис. 5.20.

Найдем связь между спектральными плотностями сигналов 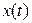и

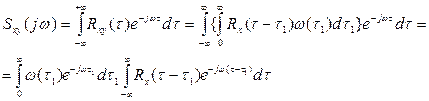(5.51)

Первый интеграл представляет собой передаточную функцию в частотной области , а второй спектральную плотность входного сигнала. Таким образом, взаимная спектральная плотность входного и выходного сигналов определяется:

(5.52)

или

(5.53)

Для спектральной плотности выходного сигнала 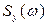справедливо следующее:

(5.54)

Заменяя первый и второй интегралы функциями и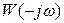, а третий спектральной плотностью 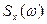, получаем

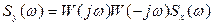(5.55)

или

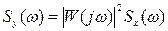(5.56)

Выражение (5.56) показывает, что спектральная плотность выходного сигнала равна спектральной плотности входного сигнала, умноженной на квадрат амплитудной частотной характеристики системы.

Фазовая характеристика системы не влияет на спектральную плотность выходного сигнала.

Таким образом, преобразование линейной системы случайного входного сигнала в случайный выходной сигнал в частотной области связано с спектральными и взаимной спектральной плотностями и может быть представлено в виде схемы (Рис. 5.21).

Рис. 5.21

Дисперсия выходного сигнала 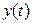может быть определена по формуле:

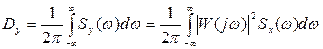(5.57)

Пример

Вычислить дисперсию на выходе апериодического звена, если на входе действует белый шум с ограниченной спектральной плотностью.

Дисперсия выходного согласно (57) имеет вид:

Из полученного выражения видно, что 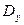тем меньше, чем меньше интенсивность входного сигнала и чем больше постоянная времени

Дата добавления: 2014-01-07