КАТЕГОРИИ:
Архитектура-(3434) Астрономия-(809) Биология-(7483) Биотехнологии-(1457) Военное дело-(14632) Высокие технологии-(1363) География-(913) Геология-(1438) Государство-(451) Демография-(1065) Дом-(47672) Журналистика и СМИ-(912) Изобретательство-(14524) Иностранные языки-(4268) Информатика-(17799) Искусство-(1338) История-(13644) Компьютеры-(11121) Косметика-(55) Кулинария-(373) Культура-(8427) Лингвистика-(374) Литература-(1642) Маркетинг-(23702) Математика-(16968) Машиностроение-(1700) Медицина-(12668) Менеджмент-(24684) Механика-(15423) Науковедение-(506) Образование-(11852) Охрана труда-(3308) Педагогика-(5571) Полиграфия-(1312) Политика-(7869) Право-(5454) Приборостроение-(1369) Программирование-(2801) Производство-(97182) Промышленность-(8706) Психология-(18388) Религия-(3217) Связь-(10668) Сельское хозяйство-(299) Социология-(6455) Спорт-(42831) Строительство-(4793) Торговля-(5050) Транспорт-(2929) Туризм-(1568) Физика-(3942) Философия-(17015) Финансы-(26596) Химия-(22929) Экология-(12095) Экономика-(9961) Электроника-(8441) Электротехника-(4623) Энергетика-(12629) Юриспруденция-(1492) Ядерная техника-(1748)
Ответ: отношение нестрого порядка, отношения предшествования Отношение нестрогого порядка
Ответ: Это отношения эквивалентности
Мощность этой системы называется
индексом разбиения множества М на классы
и определяет отношение " входить в один и тот же класс данного разбиения ".
Пример 1. К каким типам отношений относятся:
1) отношение равносильности на множестве формул,
описывающих элементарные функции
формулы равносильны, если они задают одну и ту же функцию,
например (а + b) х (а - b) = a2 - b2 ,
sin2 а + cos2 b = 1;
Ответ: Это отношения эквивалентности на соответствующих множествах .
Пример 2
отношение, определяемое на множестве всех программ
{(a,b):a и b вычисляют одну и ту же функцию на определенной машине};
Отношения порядка
рефлексивно
антисимметрично
транзитивно
Отношение строгого порядка
антирефлексивно
антисимметрично
транзитивно
на множестве людей
"быть не старше",
на множестве людей
"быть моложе",
на множестве натуральных чисел
"быть не больше"
на множестве людей
"быть прямым потомком"
Элементы а,bÎМ сравнимы по отношению порядка Rна М, если выполняется a R b или b R а
Множество М, на котором задано отношение порядка, может быть:
частично упорядоченным множеством
полностью упорядоченным множеством
отношение R задает на множестве М частичный порядок
если любые два элемента из М сравнимы по отношению порядка
для пары сотрудников одного отдела отношение "быть начальником" не выполняется:
отношение R задает полный порядок на множестве М
они не сравнимы по отношению
"быть не старше"
Пример 3
отношения £ n п с компонентами из N , определяемые следующим образом:
а) (a1 ,..., ап ) £ (b1 ..., bп ), если a1 £ b1, …, ап £ bп
Ответ: отношение £ нестрого порядка
Пример 3
б) (a1 ,..., ап ) < (b1 ..., bп ), если a1 < b1, …, ап £ bп
и хотя бы в одной координате i выполняется аi < bi
Пример 4
Oтношение предшествования букв
аi j , если аi предшествует аj в списке букв;
Ответ: - отношения строго порядка
Пример 5
Oтношение предшествования слов
Пусть даны слова a1 = а11 а12 ...а1т и a2 = а21 а22 ...а2п ,
тогда: a1 2 , если и только если
а) a1 = b аi g, a2 = b аj d и аi j , гдеb, g, d — некоторые слова,
возможно пустые; аi и аj - буквы, либо
б) a2 = a1 b, где b - непустое слово.
Ответ: отношения строго порядка
Пример 2. Проиллюстрировать диаграммой Венна следующие разбиения множества U:
а){А,
б) {А Ç В, А Ç
в) {А\В, А Ç В,В\А}.
Дата добавления: 2014-01-07 ; Просмотров: 942 ; Нарушение авторских прав? Мы поможем в написании вашей работы!
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
studopedia.su - Студопедия (2013 - 2025) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! Последнее добавление
Генерация страницы за: 0.007 сек.

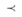 конечного алфавита А (например, отношение предшествования букв русского алфавита, отношение предшествования чисел 0, 1,2,…,9 и т.п.), заданного фиксированным списком:
конечного алфавита А (например, отношение предшествования букв русского алфавита, отношение предшествования чисел 0, 1,2,…,9 и т.п.), заданного фиксированным списком: аj, если аi предшествует аj в списке букв;
аj, если аi предшествует аj в списке букв;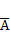 };
}; ,
,  Ç В,
Ç В,