
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные понятия. Раздел 2. Математическая логика Логические представления · описание исследуемой системы · процесса · явления в виде высказываний V
|
|
|
|
Лекция
Раздел 2. МАТЕМАТИЧЕСКАЯ ЛОГИКА
| Логические представления | · описание исследуемой системы · процесса · явления в виде высказываний v элементарных v совокупности сложных составленных из простых v и логических связок между ними | ||
| Логические представления характеризуют свойства и набор допустимых преобразований над ними v операции v и правила вывода Логические представления составляют из символов по средствам, которыхреализуют законы логики - правильные методы рассуждения, разработанные в формальной математической логике. | |||
| Глава 4. ЛОГИКА ВЫСКАЗЫВАНИЙ | |||
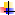 это способы это способы
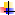 и правила формального представления высказываний и правила формального представления высказываний
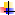 построение новых высказываний из уже имеющихся с помощью логически выдержанных преобразовании построение новых высказываний из уже имеющихся с помощью логически выдержанных преобразовании
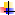 методы установления истинности или ложности высказываний методы установления истинности или ложности высказываний
| |||
Математическая логика включает два раздела:
1. логика высказываний
2. логика предикатов
Рис. 4.1
| |||
| Для построения логики высказываний и логики предикатов ввели два способа, два языка, на основе которых базируются формальная логика - алгебра логики и логические исчисления. Между понятиями языков формальной логики имеет место взаимно однозначное соответствие – изоморфизм, который обеспечивает единство законов логики, и допустимых преобразований | |||
| Основной объект логики – высказывание это повествовательное предложение, утверждение, суждение, о котором можно говорить, что оно истинно или ложно. Все научные знания: законы, явления в физике, химии, биологии, математические теоремы, события повседневной жизни, ситуации, возникающие в экономике и процессах управления, формулируют в форме высказывания. Повелительные, вопросительные и бессмысленные предложения не высказывания. | |||
 
|  “Дважды два - четыре” “Дважды два - четыре”
 “Регистрация фирмы требует наличия ее устава” “Регистрация фирмы требует наличия ее устава”
 “Мы живем в XXI веке”, “Рубль - российская валюта”, “Алеша - брат Олега” “Мы живем в XXI веке”, “Рубль - российская валюта”, “Алеша - брат Олега”
 “Операции объединения, пересечения и дополнения являются булевыми операциями над множествами” “Операции объединения, пересечения и дополнения являются булевыми операциями над множествами”
 “Человек смертен” “Человек смертен”
 “От перестановки мест слагаемых сумма не меняется” “От перестановки мест слагаемых сумма не меняется”
 “Сегодня понедельник” “Сегодня понедельник”
 “Если идет дождь, вам следует взять зонт” “Если идет дождь, вам следует взять зонт”
| ||
| Для операций над предложениями как высказываниями надо знать истинность каждогопредложения. В ряде случаев истинность или ложность высказывания зависит от описания конкретной реальности, системы, процесса, явления, тогда говорят: - Данное высказывание истинно (ложно) в данной интерпретации (данном контексте) и предполагают, что контекст задан и высказывание истинно. | |||
Высказывание простое (элементарное), если его нельзя уменьшить и можно интерпретировать как смысловой элемент множества, не содержащий логических связок.
Сложным (составным) называется высказывание, составленное из простых высказываний с помощью логических связок.
В речи, при описании явления, роль связок при составлении из простых предложений сложных высказываний используют часть речи союзные слова “и”, “или”, “не”;
слова “если..., то”, “либо... либо” (в разделительном смысле), “тогда и только тогда, когда” и др.
В логике высказываний в сложном высказывании значение связки определяют однозначно, и это дает основание для перехода к операциям логики высказываний.
Операции логики высказываний
Конъюнкция (операция “И”, логическое произведение) двух высказываний Р и Q это высказывание, истинно, если оба высказывания истинны, и ложное - во противном случае. Обозначают: P&Q; Р Ù Q, P·Q
Читают: “Р и Q”.
Дизъюнкция (операция "ИЛИ”, логическая сумма) двух высказываний Р и Q это высказывание, ложное в случае, когда оба высказывания ложны, и истинное - во всех других случаях.
Обозначают: Р Ú Q, Р + Q
Читают: “Р или Q";
Понимают: неразделительное “или”.
Отрицание (инверсия) высказывания Р это высказывание, истинное, если высказывание Р ложно, и ложное - в противном случае. Обозначают:  , ØР
, ØР
Читают: “не Р”
“неверно, что Р”.
Импликация (логическое, следование) двух высказываний Р и Q это высказывание, ложно, когда Р истинно, a Q ложно; во всех других случаях - истинное.
Обозначают: Р ® Q, P É Q
Читают: “если Р, то Q”,
“Р влечет Q”,
“из Р следует Q”
Называют: Высказывание Р - посылкой импликации
Высказывание Q - заключением.
Эквивалентность (эквиваленция, равнозначность) двух высказываний Р и Q это высказывание, истинно, когда истинные значения Р и Q совпадают, и ложное - в противном случае.
Обозначают: Р ~ Q, P º Q, Р «Q
Читают: “Р эквивалентно Q",
“Р, если и только если Q",
“Р равнозначно Q”.
Неравнозначность (исключающее “ИЛИ”, сложение по модулю 2) двух высказываний Р и Q это высказывание, истинно, когда истинные значения Р и Q не совпадают, и ложное - в противном случае.
Обозначают: Р Å Q, РD Q
Читают: “либо P либо Q”
“или Р или Q”
Понимают - в разделительном смысле.
Буквы, обозначающие высказывания, логические связки и скобки составляют алфавит языков логики высказываний, алгебры логики и исчисления высказываний.
С помощью алфавита можно построить логические формулы.
Пример: более точное определение логической формулы, как в математической логике.
Выражение, составленное из обозначений, высказываний и связок, скобок называют- логической формулой, если оно удовлетворяет условиям:
· любая переменная, обозначающая высказывание - формула,
· если А и В - формулы, то
(А & В) конъюнкция произведение
(Р Ú Q) дизъюнкция сложение
(ùА) инверсия отрицание
(P®Q) импликация следование
(P~ Q) эквиваленция равнозначность
(Р Å Q) неравнозначность сложение по модулю 2
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 422; Нарушение авторских прав?; Мы поможем в написании вашей работы!

