Векторное произведение двух векторов. Рассмотрим три некомпланарных вектора

Рассмотрим три некомпланарных вектора

Определение. Упорядоченная тройка векторов образует правую (левую) связку, если кратчайший поворот первого вектора до совмещения со вторым вектором в плоскости этих векторов происходит против движения (по движению) часовой стрелки, если смотреть с конца третьего вектора .

Рис. 11.1. Правая связка

Определение. Векторным произведением вектора на вектор называют вектор , удовлетворяющий условиям:

1) ; (11.1)

2) ;

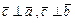3) – правая связка.

Замечания. 1. Условие 1) определения задает длину вектора, а условия 2) и 3) – направление.

2. Из условия 1) определения векторного произведения двух векторов следует, что модуль векторного произведения двух векторов численно равен площади параллелограмма, построенного на векторах-сомножителях.

Рис. 11.2.

Теорема 11.1. Векторное произведение двух векторов равно нулю тогда и только тогда, когда векторы коллинеарны.

Доказательство: Необходимость. Пусть

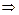
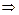
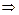
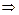
А так как имеет произвольное направление, то

Достаточность. Пусть

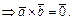
ч.т.д.

ì Следствие. . (11.2)

Свойства векторного умножения двух векторов:

1 º. ;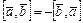

2 º. ;

3 º. , .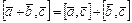

ìИз указанных свойств следует, что векторное произведение одной линейной комбинации векторов на другую линейную комбинацию производится аналогично умножению одного многочлена на другой с учетом свойства антикоммутативности векторного умножения.

Пример. Найти площадь параллелограмма, построенного на векторах и , если

Решение. Используя определение векторного произведения двух векторов, получаем:

Ответ: .

Рассмотрим связь между векторным и скалярным произведениями двух векторов и .

Поскольку имеют место соотношения

и .

Поэтому нетрудно показать, что

.

А так как , , а значит и , то

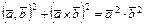. (11.3)

Равенство (11.3) называют основным соотношением векторной алгебры.

Дата добавления: 2014-01-07