Преобразования Галилея

Инерциальные системы отсчета. Принцип относительности Галилея.

Рассмотренные ранее переходы от декартовой к сферической, цилиндрической или другой системе координат относятся к одной и той же системе отсчета. Это простые геометрические преобразования.

Связь систем отсчета, находящихся в движении относительно друг друга, это физическая задача.

Система отсчета, движущаяся поступательно равномерно и прямолинейно, называется инерциальной системой отсчета. В инерциальных системах отсчета выполняются законы инерции Ньютона.

Из многочисленных экспериментов известно, что в инерциальных системах координат все механические явления протекают одинаково – это постулат относительности Галилея (Галилео Галилей, 1564 – 1642, Италия).

Это постулат, т.к.:

1. подтверждается физическими экспериментами, которые являются точными;
2. «все» явления еще не открыты;

В момент t=0 начала систем отсчета совпадают, а в момент t K’ находится в точке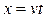

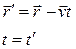преобразования Галилея

Пусть не штрихованная система движется относительно штрихованной системы со скоростью . Тогда:

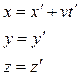
Величины, численные значения которых не изменяются при преобразованиях – инварианты. При преобразованиях изменяются варианты (скорость, импульс, координаты).

Рассмотрим, как ведет себя длина тел при преобразованиях Галилея.

Пусть в штрихованной системе находится стержень с координатами

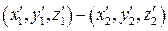
Его длина в неподвижной системе отсчета:

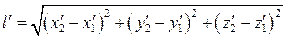
В движущейся системе отсчета: засекли концы движущегося стержня одновременно. Длина движущегося стержня:

Воспользуемся формулами преобразования Галилея:

1. Поскольку , то длина тела – инвариант.
2. При выводе преобразований Галилея считаем, что время абсолютно и неизменно для всех систем отсчета. Это интуитивное предположение примем без доказательства. В классической механике оно считалось естественным, само собой разумеющимся.
3. Одновременность двух событий имеет абсолютный характер, независимый от системы отсчета. Отсюда вытекает инвариант времени:

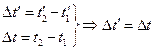
Дата добавления: 2014-01-07