Описание магнитного поля в магнетиках. Напряженность и индукция магнитного поля. Магнитная восприимчивость и магнитная проницаемость вещества

Намагниченное вещество создает магнитное поле 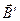, которое накладывается на внешнее поле 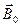(поле в вакууме). Оба поля в сумме дают результирующее магнитное поле с индукцией

,

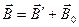причем под 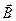здесь и далее подразумевается макроскопическое (усредненное по физически бесконечно малому объему вещества) поле.

В силу замкнутости силовых линий поле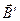й и 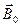, поток результирующего поля 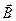через произвольную замкнутую поверхность S равен нулю:

.

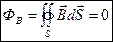Таким образом, теорема Гаусса в применении к магнетикам имеет такой же вид, как и в вакууме.

Обратимся теперь к циркуляции вектора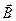по замкнутому контуру. Согласно теореме о циркуляции магнитного поля:

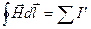или ,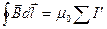

где под 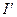следует понимать теперь сумму как макроскопических, так и молекулярных токов, то есть

.

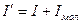Сумма всех молекулярных токов, охваченных контуром интегрирования, есть:

.

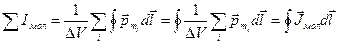Следовательно, можем написать:

.

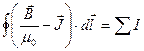Величину, стоящую в круглых скобках под знаком интеграла, обозначают буквой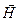и называют напряженностью магнитного поля:

.

Теперь мы можем записать теорему о циркуляции магнитного поля как:

,

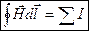где под 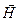понимается введенная выше величина, характеризующая напряженность магнитного поля в веществе.

Согласно написанному равенству, циркуляция вектора напряженности магнитного поля по некоторому замкнутому контуру равна алгебраической сумме макроскопических токов, охваченных этим контуром.

Из сказанного следует, что вектор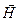является аналогом вектора электрической индукции 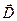. Первоначально предполагалось, что в природе имеются подобные электрическим зарядам «магнитные заряды», и учение о магнетизме развивалось по аналогии с учением об электричестве. Тогда же были введены названия «электрическая индукция» для 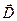и «магнитная индукция» для 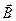. Позже, однако, выяснилось, что в природе «магнитных зарядов» нет и в действительности магнитная индукция 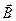является аналогом не 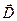, а напряженности электрического поля 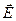; соответственно напряженность магнитного поля 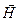– аналогом индукции электрического поля.

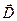Итак, индукция магнитного поля есть:

.

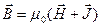Вектор намагничивания 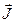принято связывать не с магнитной индукцией 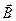, а с напряженностью магнитного поля 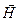, и как показывает опыт, вектор 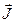связан с вектором 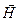соотношением:

,

где χ – характерная для данного магнетика величина, называемая магнитной восприимчивостью.

Поскольку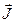имеет ту же размерность, что и 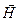[A/м], то χ – безразмерная величина. На основании двух последних формул имеем:

,

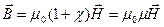где через

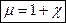
обозначена величина, называемая магнитной проницаемостью.

Дата добавления: 2014-01-07