Алгоритмы поиска путей в графе

Графы

Графы - обобобщение структуры деревьев. Граф обычно определяется как некоторое множество точек (называемых вершинами) и некоторое множество линий (называемых ребрами), соединяющих определенные пары вершин. Каждая пара вершин соединяется не больше чем одним ребром.

Можно рассматривать взвешенные и невзвешенные, ориентированные и неориентированные графы. Граф, в котором нет кратных ребер, можно задать при помощи весовой матрицы. Для каждой пары вершин в матрице указывается вес ребра, соединяющего вершины (если ребра нет, то полагаем соответствующий элемент матрицы равным бесконечности). Матрица может быть несимметричной в случае ориентированного графа. В случае невзвешенного графа удобнее представлять его при помощи матрицы связности, элемент которой равен 1, если есть соответствующие ребро, и 0, если ребро отсутствует. Пример использования графа – это задание условий в задаче коммивояжера, причем населенные пункты помещаются в вершины графа, а веса ребер определяют расстояние между соответствующими населенными пунктами.

Теория графов достаточно обширна и многие алгоритмы, рассматриваемые в ней, имеют интерес сами по себе. Для решения прикладных задач часто возникает необходимость определить связаны ли две вершины графа, а в случае наличия весов, определить еще и вес пути между ними.

Граф (свободное дерево) обычно определяется как некоторое множество точек (называемых вершинами или узлами) и некоторое множество линий, называемых ребрами (или дугами), соединяющих определенные пары вершин. Каждая пара вершин соединяется не больше чем одним ребром. Дуга, соединенная с вершиной, называется инцидентной этой вершине. Две вершины называются смежными, если существует ребро, соединяющее их. Две дуги называются смежными, если они инцидентны одной и той же вершине.

Пусть V и V` - вершины и пусть n ³0; говорят, что «V<sub>0</sub>, V<sub>1</sub>, …, V<sub>n</sub>» - путь длины n от V до V `, если V=V₀, вершина V_k смежна с V_k+1 при 0£ k < n, а V_n=V`. Путь прост, если вершины V₀, V₁, …, V_n-1 все различны между собой, а также различны все вершины V₁, V₂, …, V_n. Граф называется связным, если имеется путь между каждыми двумя вершинами этого графа. Циклом называется простой путь длины не менее 3 от какой-либо вершины до нее самой. Свободное дерево – это связный граф, не имеющий циклов.

Формально направленный граф определяется как некое множество вершин и множество дуг, причем каждая дуга ведет от некоторой вершины V к некоторой вершине V `. Если e – дуга, идущая от V к V `, то говорят, что V – начальная вершина дуги e, а V` - конечная вершина.

Рис. 1.4. Направленный и ненаправленный графы

Для задания графов существует несколько классов матриц, основные из которых класс матриц инциденции и класс матриц смежности.

Класс матриц инциденции. Если граф Г содержит n вершин и m дуг, то матрица инциденции А(Г)=[a_ij]_mxn определяется так:

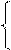1, если вершина v_j – начало дуги u_i;

a_ij = -1, если вершина v_j – конец дуги u_i;

0, если дуга u_i не инцидентна вершине v_j.

Направленный граф на рис. 6.4 можно задать матрицей инциденции:

Класс матриц смежности. Матрица смежности S=[s_ij]_nxm невзвешенного графа определяется следующим образом:

S_ij = 1, если v_i смежна v_j;

0, если вершины несмежны.

Во взвешенном графе каждая единица заменяется на вес соответствующего ребра.

Ненаправленный граф на рис. 1.4 описывается следующей матрицей смежности:

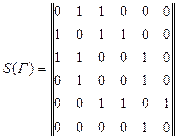
Дата добавления: 2014-01-07