КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Забезпеченя ІС
|
|
|
|
Методологія проектування інформаційного
ЩО НАВЧАЮТЬСЯ
Основна відмінність методології проектування інформаційного забезпечення ІС, що навчаються, від традиційних методологій, де виконання задач аналізу і синтезу розділено в часі, полягає в тому, що при моделюванні когнітивних процесів прийняття рішень етапи аналізу і синтезу є взаємозв’язаними, а реалізація в процесі функціонування їх задач здійснюється залежно від результатів попередніх задач.
Основними етапами аналізу при проектуванні інформаційного забезпечення ІС, що навчається, є:
- формування вхідного математичного опису ІС;
-категорійне моделювання слабо формалізованих процесів автоматичної класифікації;
- розвідувальний аналіз реалізацій образу на вході ІС.
На етапі формування вхідного математичного опису розглядаються такі задачі:
- формування словника ознак розпізнавання;
- забезпечення мінімального обсягу репрезентативної навчальної вибірки;
- визначення системи нормованих допусків (СНД) на ознаки розпізнавання, які задають область допустимих значень відповідної системи контрольних допусків (СКД).
На рис. 2.1 наведено ієрархічну структуру задач аналізу при проектуванні інформаційного забезпечення ІС, що навчаються.
Рисунок 2.1– Структура задач аналізу ІС, що навчається
Основними задачами розвідувального аналізу є:
- оцінка статистичної стійкості та однорідності навчальної вибірки з метою формування асоційованої навчальної матриці в задачах кластер-аналізу та виявлення емпіричних закономірностей даних з метою коригування алгоритму навчання ІС;
- візуалізація даних з метою як коригування алгоритмів навчання, так і вивчення тенденції покращання їх тактико-технічних характеристик точності, оперативності та надійності; оцінка релевантності даних з метою виявлення інформативних, аномальних, заважаючих (дезінформуючих) і латентних ознак.
|
|
|
На рис.2.2 наведено структуру задач синтезу інформаційного забезпечення здатної навчатися ІС у рамках ІЕІ-технології.
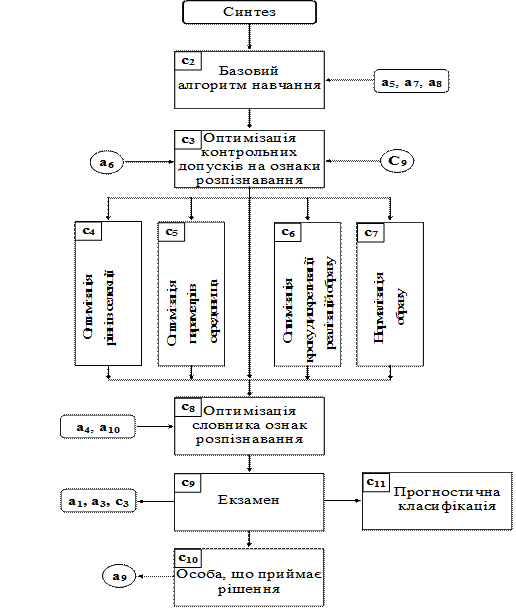
Рисунок 2.2– Структура задачі інформаційного синтезу ІС
За об’єктно-орієнтованою методологією проектування як прабатьківський об’єкт на рис. 2.2 розглядається базовий алгоритм навчання, а всі інші алгоритми успадковують його дані та методи з відповідним їх довизначенням. Оскільки структура задач, показаних на рис. 2.2, претендує на функціональну повноту, яка забезпечує побудову безпомилкових за навчальною матрицею вирішальних правил, то на практиці реалізація алгоритмів навчання всіх ієрархічних рівнів не є обов’язковою за умови, що інформаційний КФЕ набуває свого максимального граничного значення в робочій області визначення його функції вже на попередньому рівні.
Серед показаних на рис. 2.1 і рис. 2.2 зв’язках проаналізуємо зворотні зв’язки між об’єктом “Екзамен” і об’єктами “Розвідувальний аналіз” 
і “Оптимізація контрольних допусків на ознаки розпізнавання” 
. Наявність першого зв’язку обумовлена необхідністю аналізу вхідних даних з метою виявлення причин зниження повної достовірності класифікації на екзамені, а необхідність іншого зв’язку 
, який має рекурсивний тип, виникає в задачах кластер-аналізу, коли здійснюється донавчання СППР.
Таким чином, методологія розроблення інформаційного забезпечення СППР, що навчається, в рамках ІЕІ-технології полягає у розробленні взаємозв’язаного, взаємозалежного і взаємообумовленого процесу реалізації методів аналізу і синтезу, що принципово відрізняється від систем, побудованих за операторним принципом функціонування.
|
|
|
2.2 Основні положення ІЕІ-технології
Основна ідея машинного навчання у рамках ІЕІ-технології полягає в трансформації апріорного у загальному випадку нечіткого розбиття простору ознак у чітке розбиття класів еквівалентності шляхом ітераційної оптимізації параметрів функціонування ІС. При цьому здійснюється цілеспрямовано пошук глобального максимуму багатоекстремальної функції статистичного інформаційного критерію в робочій (допустимій) області її визначення і одночасного відновлення оптимальних роздільних гіперповерхонь, що будуються в радіальному базисі бінарного простору ознак розпізнавання. Відмінністю методів ІЕІ-технології є те, що трансформація вхідного нечіткого розподілу реалізацій образів в чітке здійснюється в процесі оптимізації системи контрольних допусків, що приводить до цілеспрямованої зміни значень ознак розпізнавання і дозволяє побудувати безпомилкові за багатовимірною навчальною матрицею вирішальні правила.
Таким чином, у рамках ІЕІ-технології вдалося поєднати нормалізацію образів, яка полягає у виправленні їх апріорної деформації стосовно еталонного образу, і безпосередньо етап навчання, на якому будуються вирішальні правила.
Нехай відомий алфавіт класів розпізнавання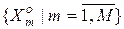 
. У загальному випадку при прийнятті гіпотези нечіткої компактності реалізацій образу розбиття простору ознак на класи розпізнавання є нечітким розбиттям 
, яке відповідає умовам:
1) 
2) 
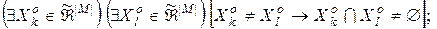
3)
4)
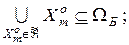
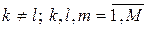. (2.2.1)
При цьому елементи розбиття є нечіткими класами розпізнавання.
У бінарному просторі ознак 
формою оптимального контейнера класу розпізнавання є гіперпаралелепіпед. З метою узагальнення та зручності побудови такого контейнера припустимо існування “псевдогіперсфери”, яка описує гіперпаралелепіпед, тобто містить усі його вершини. Це дозволяє далі розглядати такі параметри оптимізації контейнера в радіальному базисі простору ознак , як еталонний вектор, наприклад,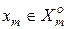 
, вершина якого визначає геометричний центр контейнера 
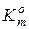, і радіус псевдосферичного контейнера, який визначається у просторі Хеммінга за формулою
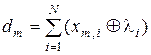, (2.2.2)
де 
- i- та координата еталонного вектора 
; 
- i -та координата деякого вектора 
, вершина якого належить контейнеру 
.
|
|
|
Надалі, з метою спрощення, кодова відстань (2.2.2), наприклад, між векторами і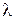 
буде позначатися у вигляді 
.
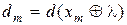За ІЕІ-технологією відновлення оптимального контейнера в радіальному базисі, наприклад, 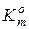здійснюється шляхом його цілеспрямованої послідовної трансформації в гіперсферичний габарит, радіус 
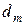якого збільшується на кожному кроці навчання за рекурентною процедурою:
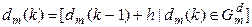, (2.2.3)
де 
змінна числа збільшень радіуса контейнера ;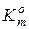 
крок збільшення радіуса;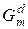 
– область допустимих значень радіуса .
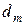Нехай класи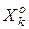 
і 
є “найближчими сусідами”, тобто мають серед усіх класів найменшу міжцентрову відстань 
, де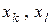 
- еталонні вектори відповідних класів. Тоді за ІЕІ-технологією з метою запобігання “поглинання” одним класом ядра іншого класу умови (2.2.1) доповнюються таким предикатним виразом:
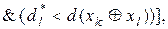(2.2.4)
де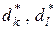 
- оптимальні радіуси контейнерів 
і 
відповідно.
Алгоритм навчання за ІЕІ-технологією полягає в реалізації багатоциклічної ітераційної процедури оптимізації структурованих просторово-часових параметрів функціонування ІС шляхом пошуку глобального максимуму усередненого за алфавітом 
значення КФЕ навчання.
Нехай вектор параметрів функціонування ІС у загальному випадку має таку структуру:
(2.2.5)
де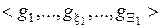 
– генотипні параметри функціонування ІС, які впливають на параметри розподілу реалізацій образу; 
– фенотипні параметри функціонування ІС, які прямо впливають на геометрію контейнера класу розпізнавання.
При цьому відомі обмеження на відповідні параметри функціонування:
; 
.
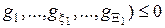У рамках методології об’єктно-орієнтованого проектування подамо тестовий алгоритм навчання за ІЕІ-технологією для загального випадку (М >2) як ієрархічну ітераційну процедуру оптимізації структурованих просторово-часових параметрів (2.2.5) функціонування ІС:
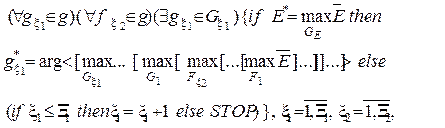(2.2.6)
де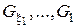 
- області допустимих значень відповідних генотипних параметрів навчання;
–
усереднене значення КФЕ навчання ІС; 
– область значень функції інформаційного КФЕ навчання; 
- оптимальне значення параметра навчання, яке визначається у зовнішньому циклі ітераційної процедури оптимізації;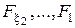 
– області допустимих значень відповідних фенотипних параметрів навчання. Тут 
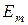– інформаційний КФЕ навчання ІС розпізнавати реалізації класу 
.
|
|
|
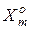Глибина циклів оптимізації визначається кількістю параметрів навчання у структурі (2.2.5). При цьому внутрішні цикли оптимізують фенотипні параметри навчання, які безпосередньо впливають на геометричну форму контейнерів класів розпізнавання. Такими параметрами, наприклад, для гіперсферичних контейнерів класів є їх радіуси. До генотипних відносять параметри навчання, які прямо впливають на розподіл реалізацій класу (наприклад, контрольні допуски на ознаки розпізнавання, рівні селекції координат еталонних двійкових векторів, параметри оптимізації словника ознак, плану навчання, параметри впливу середовища та інше). Послідовна оптимізація кожного із цих параметрів дозволяє збільшувати значення максимуму КФЕ навчання, що підвищує повну ймовірність правильного прийняття рішень на екзамені. Обов’язковою процедурою алгоритму навчання за ІЕІ-технологією є оптимізація контрольних допусків, величина яких безпосередньо впливає на значення відповідних ознак розпізнавання, а так само і на параметри розподілу реалізацій образу.
При компараторному розпізнаванні (М =2), яке відбувається шляхом порівняння образу, що розпізнається, з еталонним образом і має місце, наприклад, в задачах ідентифікації кадрів, самонаведенні літальних апаратів, класифікаційному самонастроюванні та інше, ітераційний алгоритм навчання за ІЕІ-технологією має такий структурований вигляд:
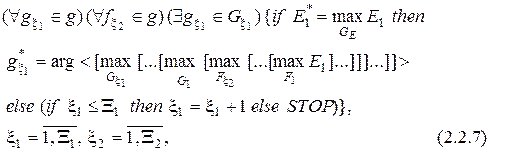
де 
– інформаційний КФЕ навчання ІС розпізнавати реалізації еталонного класу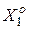 
.
Таким чином, за умови обґрунтування гіпотези компактності (чіткої або нечіткої) основна ідея навчання за ІЕІ-технологією полягає в послідовній нормалізації вхідного математичного опису ІС шляхом цілеспрямованої трансформації апріорних габаритів розкиду реалізацій образів з метою максимального їх захоплення контейнерами відповідних класів, що відбудовуються в радіальному базисі у процесі навчання. Оптимальні контейнери за ІЕІ-технологією забезпечують максимальну різноманітність між сусідніми класами, міра якої дорівнює максимуму інформаційного КФЕ навчання в робочій області визначення його функції. Оптимальні геометричні параметри контейнерів, одержані в процесі навчання за ІЕІ-технологією, дозволяють на екзамені приймати рішення за відносно простим детермінованим вирішальним правилом, що важливо при реалізації алгоритмів прийняття рішень в реальному темпі часу. При цьому повна достовірність класифікатора наближається до максимальної асимптотичної, яка визначається ефективністю процесу навчання. Досягнення на екзамені асимптотичної достовірності розпізнавання можливо за умови забезпечення однакових характеристик статистичної стійкості та статистичної однорідності навчальної та екзаменаційної матриць. Виконання цієї умови має місце при навчанні ІС безпосередньо у процесі функціонально-статистичних випробувань.
Цілеспрямованість оптимізації просторово-часових параметрів функціонування ІС за ІЕІ-технологією здійснюється шляхом визначення тенденції зміни асимптотичних точнісних характеристик процесу навчання.
2.3 Формування вхідного математичного опису
Основною задачею формування вхідного математичного опису ІС є створення багатовимірної навчальної матриці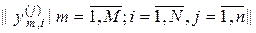 
. При цьому необхідно розв’язувати такі задачі:
· формування словника ознак та алфавіту класів розпізнавання;
· визначення мінімального обсягу репрезентативної навчальної матриці;
· визначення нормованих допусків на ознаки розпізнавання.
Таким чином, формування вхідного математичного опису ІС потребує детального вивчення та аналізу особливостей функціонування джерела інформації, яким, наприклад, у задачах керування може бути розподілений у просторі і часі технологічний процес, космічний корабель та інше.
Вхідний математичний опис подамо у вигляді теоретико-множинної структури
DВ=< G, T, , Z, Y; П, Ф >, (2.3.1)
де G - простір вхіднихсигналів (факторів), які діють на ІС; T - множина моментів часу зняття інформації;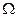 
- простір ознак розпізнавання; Z– простір можливих станів ІС; Y - множина сигналів, які знімаються з виходу БПОІ;
П: G
T
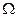
Z - оператор переходів, що відбиває механізм зміни станів ІС під впливом внутрішніх і зовнішніх факторів; Ф: GT
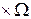
Z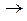
Y - оператор формування вибіркової множини Y на вході ІС.
Таким чином, як універсум випробувань W розглядається декартовий добуток наведених в (2.3.1) множин:
W = GTZ.
Словник ознак розпізнавання 
, де 
, складається з первинних ознак, які є безпосередньо характеристиками процесу, що досліджується, і з вторинних ознак, які є похідними від первинних. Обов’язковою вимогою до словника ознак є його структурованість. На практиці первинними ознаками можуть бути значення параметрів, що зчитуються з датчиків інформації, або експериментальні дані, одержані безпосередньо при дослідженні процесу, включаючи умови його реалізації. Найбільш поширеними вторинними ознаками є різні статистичні характеристики векторів-реалізацій класів 
, навчальних вибірок 
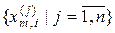або всієї навчальної матриці.
Формування алфавіту класів розпізнавання 
може здійснюватися як розробником інформаційного забезпечення, так і безпосередньо ІС, що здатна функціонувати в режимі кластер-аналізу. При цьому варто враховувати, що збільшення потужності алфавіту при незмінному словнику ознак розпізнавання суттєво впливає на асимптотичні точнісні характеристики, що характеризують функціональну ефективність навчання системи, через збільшення ступеня перетину класів розпізнавання.. Один із найпростіших імовірнісних критеріїв перетину класів для заданого алфавіту може бути подано як відношення помилки другого роду до першої достовірності, яке обчислюється на 
-му кроці ітераційного навчання:
.
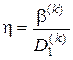Одним з ефективних шляхів корекції точнісних характеристик при збільшенні потужності алфавіту класів є формування ієрархічних алгоритмів навчання ІС, що дозволяє кількість класів розбити на групи меншої потужності і здійснювати навчання для кожної із них, та створення штучної надлишковості словника ознак, наприклад, із застосуванням методів завадозахищеного кодування.
2.4 Визначення мінімального обсягу репрезентативної
навчальної вибірки
Навчальна вибірка має на практиці скінченний обсяг n, що обумовлює наявність статистичної похибки e між імовірністю pi та емпіричною частотою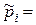 
ki n знаходження значення i -ї ознаки розпізнавання у своєму контрольному полі допусків 
. Верхня оцінка похибки e =| pi -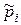 
| залежить від кількості випробувань n і визначається за теоремою Муавра-Лапласа:
(2.4.1)
де ki - кількість подій, при яких значення i -ї ознаки знаходиться в полі допусків 
; qi= 1- pi - імовірність того, що значення i -ї ознаки не належить полю допусків ; Ф(...) - функція Лапласа.
Визначення мінімального обсягу n mi n репрезентативної навчальної вибірки здійснимо за умови отримання прийнятних з практичних міркувань статистичної похибки та оперативності алгоритму його обчислення. Ці вимоги є суперечливими, що обумовлює компромісний характер розв’язання задачі. Скористаємося методом динамічного довірчого інтервального оцінювання. Суть методу полягає в побудові після кожного випробування довірчого інтервалу, який оцінює ймовірність рі знаходження i- ї ознаки в полі контрольних допусків з імовірністю довіри 1 -Q:
, (2.4.2)
де Q - рівень значущості (будь-яке наближене до нуля додатне число).
Визначення максимальної похибки e Q при заданому рівні значущості Q здійснюється із співвідношення
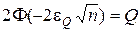. (2.4.3)
З урахуванням властивості функції Лапласа Ф(х)=1-Ф(-х) перетворимо (2.4.3) до вигляду
. (2.4.4)
Наприклад, для Q= 0.05 за таблицею значень функції Лапласа з урахуванням виразу (2.4.4) для Ф(х) = 1- Q/ 2= = 0.975 знайдемо значення аргументу функції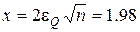 
. Тоді похибка e Q змінюється залежно від обсягу навчальної вибірки n за гіперболічним законом
. (2.4.5)
На рис. 2.3 наведено графік функції e Q = f (n) (крива 1) і умовно виділено три області значень аргументу, які відрізняються крутизною цієї функції. При цьому область І є забороненою областю, оскільки похибка перебільшує допустиму. Область ІІІ характеризується значними економічними втратами при відносно малій швидкості зменшення похибки e Q. Область II є компромісною і охоплює інтервал приблизно від 40 до 90 випробувань. Легко довести, що при різних значеннях Q графік функції e Q = f (n) буде переміщуватися паралельно по вертикалі, не змінюючи свого вигляду.
Рисунок 2.3-До визначення обсягу навчальної вибірки:
1- графік функції e Q = f (n); 2-графік емпіричної частоти 
;
3 - верхня межа довірчого інтервалу;
4 - нижня межа довірчого інтервалу
На рис. 2.3 область І є забороненою областю, оскільки похибка перебільшує допустиму. Область ІІІ характеризується значними економічними втратами при відносно малій швидкості зменшення похибки e Q. Область II є компромісною і охоплює інтервал приблизно від 40 до 90 випробувань. Легко довести, що при різних значеннях Q графік функції e Q = f (n) буде переміщуватися паралельно по вертикалі, не змінюючи свого вигляду.
Графічно довірчий інтервал можна побудувати за формулою (2.4.2), обчислюючи для кожного випробування за виразом (2.4.5) похибку e Q i відкладаючи її зверху та знизу від графіка частоти 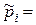ki n (крива 2). При цьому верхня 
(крива 3) та нижня 
(крива 4) межі довірчого інтервалу при збільшенні числа випробувань мають тенденцію до зближення з емпіричною частотою.
Для знаходження мінімального числа випробувань n min, яке гарантує прийнятні з практичних міркувань величину похибки і оперативність реалізації алгоритму обчислювання, необхідно задати критерій зупинення випробувань.
Таким моментом можна вважати випробування, при якому поточний довірчий інтервал накривається заданим інтервалом [0,5±D], де ½D½< 0,5. Для багатьох практичних задач значення D визначається з інтервалу [0,3;0,4] за алгоритмом, наведеним, наприклад, у праці [138]. Останній (правий) перетин заданого інтервалу з однією з меж довірчого інтервалу визначає випробування n min, яке гарантує з імовірністю 1- Q, що максимальна похибка e Q не перебільшує значення функції ε Q =f (n) при n=n min.
Таким чином, вибір n min доцільно здійснювати в компромісній області ІІ (на рис. 2.3 n min= 54) за умови відсутності викидів значень емпіричної частоти до значень, близьких до нуля або одиниці.
У загальному випадку треба будувати довірчі інтервали для всіх N ознак і вибирати n min за умови
n min =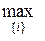
(n min 1 ,..., n min i,..., n min N).
На практиці для незалежних ознак розпізнавання можна вибирати n min за довірчим інтервалом, побудованим для будь-якої однієї ознаки, що значно знижує обчислювальну трудомісткість алгоритму.
2.5. Визначення нормованих допусків на ознаки
розпізнавання
При оптимізації процесу навчання ІС за ІЕІ-технологією важливим питанням є визначення системи нормованих допусків (СНД), яка задає області значень відповідних контрольних допусків на ознаки розпізнавання.
Визначення 2.5.1. Нормованим називається поле допусків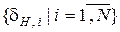 
, в якому значення і –ї ознаки знаходиться з імовірністю рі = 1 або pi= 0 за умови, що функціональний стан ІС належить до базового (найбільш бажаного для ОПР) класу 
.
Визначення 2.5.2. Контрольним називається поле допусків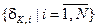 
, в якому значення і- ї ознаки знаходиться з імовірністю 0< рі <1 за умови, що функціональний стан ІС належить до базового класу .
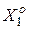У методах ІЕІ-технології контрольні допуски на ознаки розпізнавання вводяться з метою:
· рандомізації процесу прийняття рішень, оскільки для повного дослідження процесу необхідно використовувати як детерміновані, так і статистичні характеристики;
· трансформації у процесі навчання ІС параметрів розподілу реалізацій образу шляхом допустимих перетворень в дискретному просторі ознак розпізнавання.
Зрозуміло, що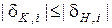 
і базова СКД є сталою для всього алфавіту класів розпізнавання. При цьому основні обмеження зверху (справа) на значення полів контрольних допусків 
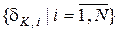повинні забезпечувати:
· збереження випадковості координат векторів-реалізацій образу;
· недопущення збігу еталонних векторів, які є центрами відповідних контейнерів класів розпізнавання, що може призвести до невиконання умов (2.2.2) або (2.2.4) розбиття простору ознак.
Відомі методи оцінки випадковості реалізацій образу обумовлюють наявність навчальної вибірки великого обсягу, що не завжди є здійсненним на практиці. Один із шляхів вирішення цієї проблеми ґрунтується на такій гіпотезі: чим більша середня кодова відстань між реалізаціями одного образу, тим більше вони будуть мати відмінних ознак розпізнавання, що свідчить про їх випадковість. Розглянемо постановку задачі оптимізації СНД за дистанційно-максимальним критерієм. Нехай 
– множина реалізацій базового, тобто найбільш бажаного для ОПР класу {
}, яку розіб’ємо на пари сусідніх векторів і визначимо кодові відстані між ними за правилом
(2.5.1)
де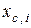 
– і -та координата реалізації 
, яка є найближчою сусідньою до реалізації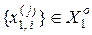 
.
Необхідно вибрати таку систему допусків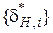 
, щоб середнє вибіркове
(2.5.2)
сусідніх реалізацій класу 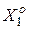було максимальним, тобто 
, якщо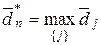 
.
Таким чином, параметром, що оптимізується, є величина симетричного поля допусків 
, центром якого є значення дискрети еталонного вектора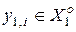 
. Алгоритм складається із послідовного проведення етапів оптимізації, на кожному з яких формується при поточній СКД множина двійкових векторів 
, здійснюється її розбиття на пари сусідніх реалізацій за умови мінімальної кодової відстані між ними, обчислюється за формулою (2.5.2) середня кодова відстань для сусідніх реалізацій і здійснюється наступний крок ітераційної процедури пошуку максимуму 
. Вхідні дані: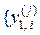 
|
– масив дискрет реалізацій, що аналізуються, де nmin – мінімальний обсяг репрезентативної навчальної вибірки; 
- змінна поля допусків; h – крок зміни поля допусків; l – змінна кроків ітерації. Результатом алгоритму оптимізації є поля нормованих допусків 
, які задають допустиму область значень контрольних допусків і цим забезпечують випадковість ознак розпізнавання.
Розглянемо схему реалізації паралельного алгоритму оптимізації нормованих допусків за критерієм (2.5.2).
1. Обчислюється еталонна реалізація дискрет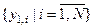 
шляхом статистичного усереднення значень дискрет реалізацій {
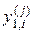} класу 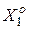і задається стартове значення параметра .
2. Формується масив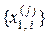 
двійкових векторів-реалізацій класу за правилом
(2.5.3)
3. Будується для векторів матриця кодових відстаней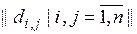 
, елементи якої визначаються за правилом
(2.5.4)
Таким чином, нульовим діагональним елементам матриці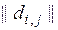 
штучно присвоюється значення 
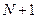– максимальна кодова відстань у матриці.
4. Формуються пари найближчих сусідніх реалізацій 
за умови, що
,
де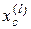 
– найближча до вектора 
реалізація, отримана на l -му кроці оптимізації.
5. Обчислюється за формулою (2.5.2) вибіркова середня відстань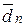 
для розбиття 
.
6. Порівнюється поточне середнє значення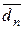 
(l) з попереднім 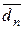(l -1). Якщо 
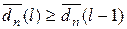, то 
, і виконується крок 1, інакше 
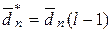і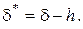 
7 Формується оптимальна СНД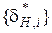 
, де нижні допуски дорівнюють 
і верхні допуски - 
.
Як приклад розглянемо визначення оптимальної за критерієм (2.5.2) системи нормованих допусків на ознаки в задачі розпізнавання спектрограм, отриманих на мас-спектрометрі МІ-12-01 АТ виробництва ВАТ “Selmi” (Суми, Україна).
На рис. 2.4 наведено дві реалізації спектрограми класу 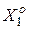. Тут на осі абсцис відкладено довжину хвилі в нанометрах, а на осі ординат – значення струму електронного підсилювача в мікроамперах.
а)
б)
Рисунок 2.4–Спектрограми: а) перша реалізація
класу ; б) друга реалізація класу
Якщо поява дискрет, значення яких перевищують шумовий поріг, відбувається детерміновано для даного хімічного елемента, то їх амплітуди, як видно з рис. 2.4, мають випадкові значення.
У табл. 2.1 наведено для прикладу сім двійкових реалізацій класу 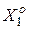, сформованих за правилом (2.5.3) при 
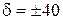. Кожна з цих реалізацій містить 12 ознак, які набувають одиничне значення, якщо значення їх дискрет перебільшують шумовий поріг.
Таблиця 2.1 – Двійкові реалізації спектрограм класу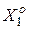
| № реалі- зації | Координати векторів | |||||||||||
| 1 | ||||||||||||
За двійковими векторами, наведеними в табл. 2.1, сформуємо за правилом (2.5.4) матрицю кодових відстаней (табл. 2.2), звідки визначимо для заданого алфавіту класів розпізнавання пари сусідніх двійкових еталонних векторів:
=<
, 
>, 
=< , >, 
=< 
, 
>,
=< 
, 
>, 
=< 
,
>, 
=< 
, 
>, 
=< , >.
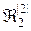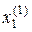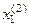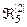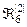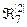Відповідно кодові відстані між сусідніми векторами дорівнюють:
d (
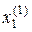
)=2; d (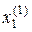)=2; d (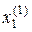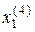)=3; d (
)=3; d (
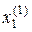)=2; d (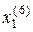
)=2; d (
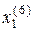)=2.
Таблиця 2.2–Матриця кодових відстаней
| k | 
|
| 
|
|
|
|
|
|
| |||||||
|
| |||||||
|
| |||||||
|
| |||||||
|
| |||||||
|
| |||||||
|
|
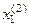
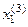
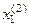
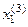
На рис. 2.5 наведено залежність середньої кодової відстані 
від параметра 
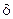поля допусків.
Рисунок 2.5 – Графік залежності середньої кодової відстані між еталонними векторами класу 
від параметра поля допусків
Аналіз рис. 2.5 показує, що область значення контрольних допусків на ознаки розпізнавання задається оптимальним значенням відповідних полів нормованих допусків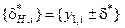 
, де 
, які гарантують випадковість реалізацій образу згідно із принципом рандомізації вхідних даних для ІЕІ-технології. При цьому система нормованих допусків знизу обмежується вимогою виключення переходу реалізацій образу в нульові. Так, вже при 
перша, друга і шоста реалізації стають нульовими. З іншого боку, при збільшенні параметра до 70 збігаються друга та четверта реалізації, що робить подальше збільшення нормованого поля недоцільним. Крім того, вибір занижених нормованих полів допусків призводить до погіршення точнісних характеристик класифікатора, а вибір завищених – до зменшення оперативності навчання. Таким чином, розроблення ефективних критеріїв оцінки випадковості навчальної вибірки у рамках ІЕІ-технології набуває важливого значення.
2.6 Оцінка статистичної стійкості та однорідності
навчальної вибірки
Важливим етапом формування навчальної вибірки є оцінка її статистичної стійкості та однорідності, оскільки ці властивості суттєво впливають на величину повної ймовірності прийняття правильних рішень. Основним способом недопущення зниження достовірності рішень, що приймає система, є блокування її функціонування як в режимах навчання, так і екзамену, якщо не виконуються умови статистичної стійкості або статистичної однорідності вибірок. У загальному випадку ІС блокує режими навчання й екзамену за таких причин:
· перехідний процес, що відбувається, наприклад, в задачах керування при зміні функціональних станів технологічного процесу під впливом як керованих, так і некерованих факторів;
· відмова технологічного обладнання;
· неправильне функціонування датчиків інформації;
· неоптимальні значення контрольних і нормованих допусків на ознаки розпізнавання.
Як критерії статистичної стійкості використовуються відомі в математичній статистиці вибіркові критерії оцінки параметрів імовірнісних розподілів [45-49]. Як критерії статистичної однорідності доцільно використовувати критерій згоди Пірсона (критерій c 2) [45,48,49], серійний критерій Вальда-Вольфсона [48], критерій Колмогорова-Смірнова (критерій l) [49], критерій серій [48,49] та інші. Як критерії інформативності ознак можуть використовуватися коефіцієнти парної та множинної кореляції [45,47] і прямі статистичні інформаційні критерії [23,43]. Одну із ієрархічних структур алгоритму прийняття рішень при оцінці статистичних стійкості та однорідності навчальної вибірки за статистичними критеріями наведено на рис. 2.6.
Аналіз рис.2.6 показує, що невиконання основної гіпотези навіть за одним будь-яким критерієм призводить до заблокування процесу формування навчальної матриці 
, а тим самим і навчання ІС.
Рисунок 2.6 – Ієрархічна структура алгоритму оцінки
статистичних стійкості та однорідності навчальної
вибірки
Таким чином, архітектура програмного забезпечення ІС, що навчається, крім інформаційних агентів «Навчання» і «Екзамен», повинна включати агента «Розвідувальний аналіз», який у процесі прийняття багатокритеріальних рішень дає дозвіл на функціонування системи у відповідному режимі.
2.7 Інформаційні критерії оптимізації параметрів
функціонування ІС, що навчається
Центральним питанням інформаційного синтезу ІС є оцінка функціональної ефективності процесу навчання, яка визначає максимальну достовірність рішень, що приймаються на екзамені. Як КФЕ в ІЕІ-технології можуть використовуватися різні критерії, які задовольняють такі властивості інформаційних мір:
· інформаційна міра є величина дійсна і знакододатна як функція від імовірності;
· кількість інформації для детермінованих змінних (
або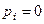 
) дорівнює нулю;
· інформаційна міра має екстремум при значенні ймовірності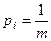 
, де m – кількість якісних ознак розпізнавання.
Серед інформаційних мір для оцінки функціональної ефективності СППР, що навчається, перевагу слід віддавати статистичним логарифмічним критеріям, які дозволяють працювати з навчальними вибірками відносно малих обсягів [50]. Серед таких критеріїв найбільшого використання знайшли ентропійні міри [51] та інформаційна міра Кульбака [52].
Подамо нормований ентропійний КФЕ навчання ІС розпізнавати реалізації класу 
у вигляді:
, (2.7.1)
де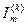 
– кількість умовної інформації, що обробляється на 
-му кроці навчанні ІС розпізнавати реалізації класу ; 
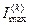– максимальна можлива кількість умовної інформації, одержаної на -му кроці навчання;
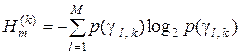– (2.4.2)
апріорна (безумовна) ентропія, що існує на -му кроці навчання системи розпізнавати реалізації класу ;
–
апостеріорна (умовна) ентропія, що характеризує залишкову невизначеність після -го кроку навчання системи розпізнавати реалізації класу 
; 
– безумовна ймовірність прийняття на -му кроці навчання гіпотези 
; 
– апостеріорна ймовірність прийняття на -му кроці навчання рішення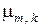 
за умови, що прийнята гіпотеза .
Для двохальтернативної системи оцінок (М = 2) і рівноймовірних гіпотез, що характеризує найбільш важкий у статистичному сенсі випадок прийняття рішень, після відповідної підстановки ентропій (2.7.2) і (2.7.3) у вираз (2.7.1) та заміни відповідних апостеріорних ймовірностей на апріорні за формулою Байєса [46] ентропійний критерій набирає вигляду
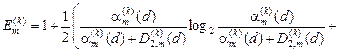
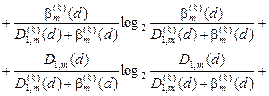
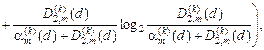(2.7.4)
де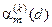 
– помилка першого роду прийняття рішення на k -му кроці навчання; 
– помилка другого роду; 
– перша достовірність; 
– друга достовірність; 
– дистанційна міра, яка визначає радіуси гіперсферичних контейнерів, побудованих в радіальному базисі простору Хеммінга.
Оскільки точнісні характеристики є функціями відстані вершин еталонних векторів від геометричних центрів контейнерів відповідних класів розпізнавання, то критерій (2.7.4) в ІЕІ-технології слід розглядати як нелінійний і взаємно-неоднозначний функціонал від точнісних характеристик, що потребує знаходження в процесі навчання робочої (допустимої) області для його визначення.
Розглянемо модифікацію диференціальної інформаційної міри Кульбака, яка подається як добуток відношення правдоподібності L на міру відхилень відповідних розподілів імовірностей.
У праці [46] розглядається логарифмічне відношення повної ймовірності 
правильного прийняття рішень про належність реалізацій класів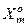 
і 
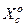контейнеру 
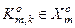до повної ймовірності помилкового прийняття рішень 
, яке для двохальтернативної системи оцінок рішень має вигляд
,
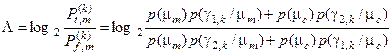(2.7.5)
де 
–безумовна ймовірність появи реалізації класу ; 
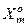–безумовна ймовірність появи реалізації найближчого (сусіднього) класу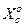 
; 
– гіпотеза про належність контейнеру 
реалізації класу ;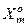 
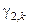– альтернативна гіпотеза.
Із урахуванням (2.7.5) при допущенні згідно із принципом Лапласа-Бернуллі, що 
, і після переозначення апріорних умовних імовірностей відповідними точнісними характеристиками загальна міра Кульбака остаточно набирає вигляду
.
(2.7.6)
Нормовану модифікацію критерію (2.7.6) можна подати у вигляді
,
де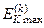 
– значення інформаційного критерію при 
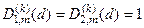і 
для формули (2.7.6).
При оптимізації параметрів функціонування ІС у процесі навчання за ІЕІ-технологією нормування критеріїв оптимізації не є обов’язковим, оскільки тут розв’язується задача пошуку екстремальних значень параметрів навчання, які відповідають глобальному максимуму КФЕ у робочій області його визначення. Але нормування критеріїв оптимізації є доцільним при порівняльному аналізі результатів досліджень і при оцінці ступеня близькості реальної ІС до потенційної.
Розглянемо процедуру обчислення модифікації ентропійного КФЕ за Шенноном для двохальтернативного рішення при рівноймовірних гіпотезах згідно з формулою (2.7.4). Оскільки інформаційний критерій є функціоналом від точнісних характеристик, то при репрезентативному обсязі навчальної вибірки необхідно користуватися їх оцінками:
; 
; 
;
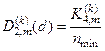, (2.7.7)
де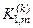 
- кількість подій, які означають належність реалізацій образу контейнеру 
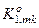, якщо дійсно 
; 
– кількість подій, які означають неналежність реалізацій контейнеру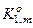 
, якщо дійсно ; 
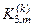- кількість подій, які означають належність реалізацій контейнеру 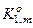, якщо вони насправді належать класу 
; 
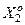- кількість подій, які означають неналежність реалізацій контейнеру 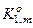, якщо вони насправді належать класу 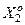; n min- мінімальний обсяг репрезентативної навчальної вибірки.
Після підстановки відповідних позначень (2.7.7) у вираз (2.7.4) одержимо робочу формулу для обчислення в рамках ІЕІ-технології ентропійного інформаційного КФЕ навчання ІС розпізнаванню реалізацій класу :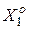
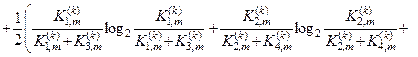
(2.7.8)
Робоча модифікація критерію Кульбака після відповідної підстановки оцінок (2.7.7) у вираз (2.7.6) набирає вигляду
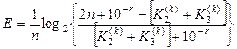
, (2.7.9)
де r - число цифр у мантисі значення критерію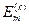 
.
Розглянемо схему обчислення коефіцієнтів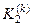 
і 
у формулі (2.7.9). На рис. 2.7 показано структуру навчальної матриці при побудові оптимального контейнера для класу 
. Навчальна матриця послідовно складається з векторів реалізацій 
і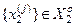 
відповідно.