Формула трапеций. Задача численного интегрирования

Задача численного интегрирования

В прикладных исследованиях часто возникает необходимость вычисления значения определенного интеграла

,

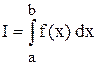К сожалению, в подавляющем большинстве случаев получить значение интеграла с помощью формулы Ньютона-Лейбница или других аналитических методов не удается. Так, интеграл 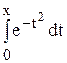широко используется при исследовании процессов массо- и теплообмена, в статистической физике и теории вероятностей. Однако его значение не может быть выражено в виде конечной комбинации элементарных функций.

При разработке численных методов нахождения значения определенных интегралов наиболее распространенным подходом является аппроксимация. Подынтегральную функцию f(x) на отрезке [a, b] приближают некоторой функцией F(x), которая легко интегрируется аналитически. Затем полагают

.

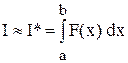Если функция f(x) задана аналитически, то ставится вопрос об оценке погрешности такой замены.

4.6.1. Вывод формулы. Пусть функция f(x) интерполируется на [a, b] многочленом 1-й степени: F(x) = P₁ (x) = y₀ + (х – x₀) ×D₁[x₀, x₁], где x₀ = a, x₁= b. Обозначим h = x₁–x₀. Или 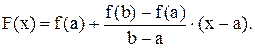Тогда

I*=.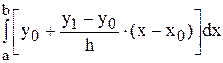

Сделаем замену переменных t = x – x₀, получим

I*== =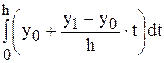

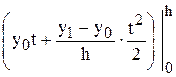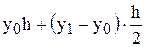
После интегрирования и преобразования получим следующую формулу:

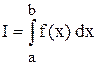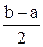» [f(a) + f(b)] = 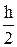[f(x₀) + f(x₁)] = I*, (4.7)

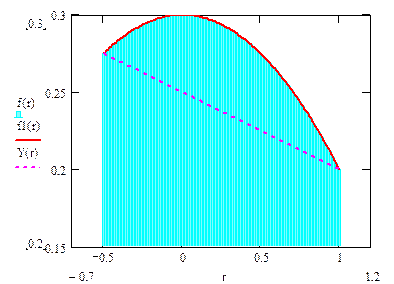
называемой формулой трапеций. Геометрически она означает замену площади криволинейной трапеции обычной трапецией (рис. 4.2), отсюда название формулы.

Рис. 4.2. Геометрическая интерпретация формулы трапеций

4.6.2. Погрешность формулы. Воспользуемся известной оценкой (3.9) погрешности интерполирования многочленом P₁(x):

R₁(z) = .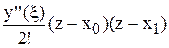

Имеем: R₁ = f(x) – F(x) Þ D = I – I* = = =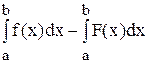

= = .

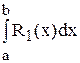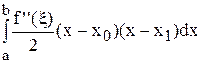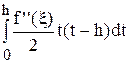Здесь мы опять сделали замену переменных t = x – x₀. Тогда x = t + x₀, а x – x₁ = t + (x₀ – x₁) = t – (x₁ – x₀) = t – h. Отсюда

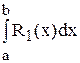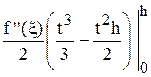= = – f ’’ (x)×.

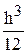Итак,

D_ТРАП = – f ’’ (x)×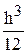, xÎ(a, b). (4.8)

Знак “–” означает, что при f ’’ > 0 формула (4.7) дает значение интеграла с избытком, а при f ’’ < 0 – с недостатком. На рис. 4.2 функция f(x) вогнута, т.е. f ’’ < 0, следовательно, I* < I. При f ’’ = 0, т.е. если f(x) = P₁(x), формула (4.7) не содержит погрешности и абсолютно точна.

Дата добавления: 2014-01-07