Оценка погрешности формулы Симпсона

Метод вывода оценки погрешности, применённый для формулы трапеции, не годится для формулы Симпсона. Поэтому без доказательства примем следующую оценку погрешности формулы (4.9):

D_СИМП = I – I* = , xÎ[ x₀, x₂]. (4.10)

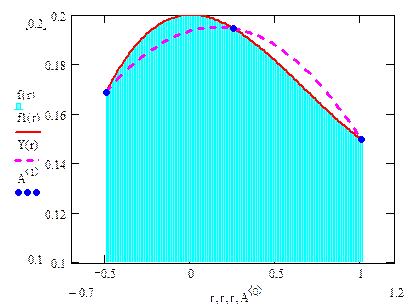
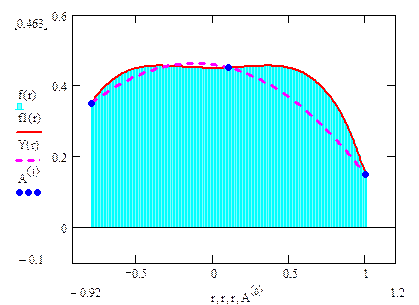
Знак “–” означает, что при f ⁽⁴⁾ > 0 формула (4.4) дает значение интеграла с избытком, а при f ⁽⁴⁾ < 0 – с недостатком. На рис. 4.4 функция f(x) представляет собой многочлен 4-й степени с постоянным значением f ⁽⁴⁾ < 0. Из рисунка видно, что площадь фигуры под графиком f(x) (окрашенная область) больше, чем под F(x). Следовательно, I* < I. При f ⁽⁴⁾ = 0, т.е. если f(x) = P₃(x), формула (4.9) не содержит погрешности и абсолютно точна. Это видно на рис. 4.3 – f(x) представляет собой многочлен 3-й степени и площади под f(x) и под F(x) абсолютно одинаков, хотя сами функции не совпадают.

Рис. 4.3. Геометрическая интерпретация формулы Симпсона

	Рис. 4.4. При f ^(4) < 0 формула Симпсона дет результат с недостатком

4.8. Составные формулы численного интегрирования

Описанные формулы численного интегрирования легко обобщить на случай применения многочленов более высоких степеней и тем самым добиться улучшения точности решения задачи (подобный метод широко применяют, при этом, в частности, получаются так называемые квадратурные формулы Ньютона-Котеса). Однако, более перспективен другой способ, основанный на кусочной аппроксимации подынтегральной функции многочленами невысокой степени.

4.8.1. Кусочно-гладкая аппроксимация функций. Пусть функция интерполируется на отрезке [a, b]. Метод решения этой задачи с помощью единого для всего отрезка многочлена Р_n (х) называют глобальной многочленной интерполяцией. При всей привлекательности перспективы иметь такой единый многочлен, существуют весьма веские причины, по которым глобальная интерполяция многочленами высокой степени в вычислительной практике, как правило, не используется.

1. Одна из основных причин этого заключается в проблеме сходимости аппроксимации при росте n. Рассмотрим пример.

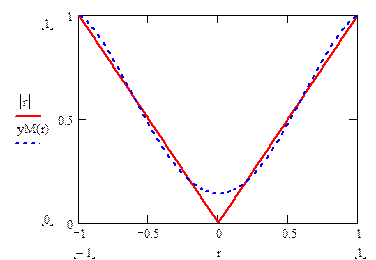
Пример 4.4. Непрерывную функцию у = | x | надо приблизить на отрезке [–1, 1] с высокой точностью. На рис. 4.5 и 4.6. приведены графики интерполяционных многочленов 5 и 13 степеней, соответственно. Видно, что при сравнительно невысокой степени n = 5 велика погрешность аппроксимации в точке х = 0. При более высоких степенях, начиная с n = 9, появляются “паразитические” всплески вблизи точек х = ±1, нарастающие при увеличении n. В результате высокая точность, порядка e = 0.001, оказывается недостижимой.

В известной степени точность глобальной многочленной интерполяции можно повысить за счет оптимального расположения узлов, однако полностью этим проблема не снимется.

Рис. 4.5. Интерполяция функции у = | x | многочленом 5-й степени

2. Вторая проблема заключается в ухудшении обусловленности задачи интерполяции при росте n, и соответственно, в повышении чувствительности к погрешности округления.

В значительной мере проблемы глобальной аппроксимации могут быть сняты применением кусочно-гладкой, в частности – кусочно-полиномиальной интерполяции. Суть подхода заключается в следующем. Исходный отрезок [ a, b ] разбивается на несколько отрезков меньшей длины, на каждом из которых функция приближается своей гладкой кривой, например, многочленом. Низкая степень многочленов гарантирует отсутствие нежелательных эффектов, подобных рассмотренным в примере 4.4, а малая величина каждого отрезка способствует увеличению точности аппроксимации. Так, в примере 4.4 исходную функцию можно абсолютно точно приблизить двумя многочленами 1-й степени на отрезках [–1, 0] и [0, 1], соответственно.

Рис. 4.6. Интерполяция функции у = | x | многочленом 13-й степени

Замечание. Подобный подход также имеет недостатки, главным из которых является негладкость интерполяционных кривых в точках “стыковки” отдельных многочленов. Данный недостаток может быть преодолен использованием так называемой сплайн-аппроксимации, при которой параметры многочленов подбираются из условия гладкости сочленения (совпадения первых производных) отдельных звеньев (сплайнов) в точках “склеивания”. Подобная интерполяция используется при решении многих задач, в частности, в компьютерной графике и машиностроении при построении линий сложной формы. На рис. 4.7 приведены графики различных видов интерполяции.

Для нужд численного интегрирования негладкость кусочной аппроксимации, вообще говоря, помехой не является, поэтому методы аппроксимации сплайнами подробно нами рассматриваться не будут.

Идея кусочно-гладкой аппроксимации в интегрировании: разбить отрезок [ a, b ] на n частей и на каждой части применить формулу трапеций или Симпсона. Из формул (4.8) и (4.10) видно, что при h < 1 погрешность этих формул уменьшается.

4.8.2. Составная формула трапеций. Разобьём отрезок [a, b] на n частей равноотстоящими точками x₀ = a, x₁ = a + h, …, x_n = b, и на каждой части [x_i, x_i+1] применим формулу трапеций:

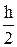» ×(y_i + y_i+1).

Получим

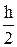» ×[(y₀ + y₁) + (y₁ + y₂) + … + (y_n–1 + y_n)] Þ

» h×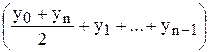– (4.11)

составная формула трапеций. Её геометрический смысл – подынтегральная функция заменяется ломанной.

4.8.3. Оценка погрешности. Очевидно, погрешность формулы (4.11) равна сумме погрешностей на каждом i-м интервале. Воспользуемся формулой (4.8), получим 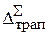= – 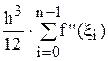, где x_iÎ[x_i, x_i+1].

Обозначим m = – среднее арифметическое значений второй производной, а также m = , M = 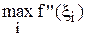. По известному свойству среднего арифметического имеем: m £ m£ M.

Из математического анализа известна 2-я теорема Больцано-Коши: если функция y(x) непрерывна на отрезке, то она принимает все свои значения, от минимального до максимального. Иными словами, для любого р, такого что min y(x) £ p £ max y(x), уравнение p = y(x) всегда имеет решение при непрерывной функции у(х). Для разрывной функции это, вообще говоря, неверно (см. рис. 4.8).

Рис. 4.8. Иллюстрация ко 2-й теореме Больцано-Коши: непрерывная и разрывная функции.

Если f’’(x) непрерывна на [a, b], то к ней применима указанная теорема при р = m. Значит, существует такая точка xÎ[a, b], что m = f’’(x). Следовательно,

= n×m = n×f ’’(x). Тогда

= – = –.

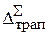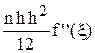Следовательно,

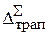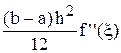= –. (4.12)

4.8.3. Составная формула Симпсона. Разобьём отрезок [a, b] на n частей, где n – чётно. Применим формулу Симпсона к каждому двойному отрезку [x_2i–2, x_2i]. Тогда

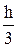» ×[(y₀ + 4y₁ + y₂) + (y₂ + 4y₃ + y₄) + … + (y_n–2 + 4y_n–1 + y_n)].

Заметим, что y₂, y₄,… y_n–2 повторяются дважды. Отсюда

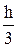» ×[(y₀ + y_n) + 4S_нечётн + 2S_чётн ] (4.13)

составная формула Симпсона.

Здесь S_нечётн = y₁ + y₃ + … + y_n–1, S_чётн = y₂ + y₄ + … + y_n–2.

4.8.4. Оценка погрешности. Для оценки погрешности формулы (4.13) воспользуемся оценкой (4.10) погрешности простой формулы. Применим тот же метод, что и для составной формулы трапеции. Получим

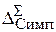= –. (4.14)

Задание. Вывести формулу (4.14) самостоятельно.

Дата добавления: 2014-01-07