Метод дробления шага. Правило Рунге. Формулы (4.12) и (4.14) для практики неудобны, т.к

Формулы (4.12) и (4.14) для практики неудобны, т.к. значения f^(k) (x) обычно неизвестны. Правило Рунге позволяет найти достаточно точные оценки погрешности, используя значения I*, вычисленные при различных h.

Согласно полученным оценкам, погрешность составных формул численного интегрирования имеет вид

I – I^h» C×h^m, (4.15)

где I и I^h – точное значение интеграла и значение, найденное по составной формуле при шаге h, соответственно; С – некоторая константа; m – порядок точности численного метода (согласно формулам (4.12) и (4.14), m = 2 для формулы трапеции и m = 4 для формулы Симпсона).

Уменьшим шаг вдвое. Будем иметь:

I – I^h/2» 2^–m×C×h^m. (4.16)

Вычтем (4.16) из (4.15). Получим: I^h/2 – I^h» 2^–m×C×h^m(2^m – 1) = (I – I^h/2)(2^m – 1).

Следовательно,

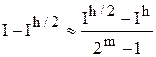. (4.17)

Формула (4.17) – оценка погрешности вычисления I^h/2 по правилу Рунге. Если значение правой части приближенного равенства (4.17) окажется меньше предельно допустимой погрешности e, то можно считать I^h/2 ответом задачи. В противном случае – требуемая точность не достигнута и необходимо использовать более мелкий шаг, т.е. продолжить процесс дробления шага.

Замечание. При приближённом вычислении интегралов, абсолютная величина | I | которых мала, использование значения абсолютной погрешности D для контроля точности необоснованно, более приемлема относительная погрешность d. Поэтому при использовании правила Рунге рекомендуется следующий критерий останова процесса дробления шага:

если | I^h/2 | ³ 1, то заканчивать при ,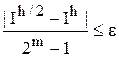

если | I^h/2 | < 1, то заканчивать при .

Пример использования правила Рунге см. «Вычислительная практика» Пример 4.4. Там же в разделе 5 приведены тестовые примеры для программ численного интегрирования.

Задание. Обобщите правило Рунге на случай, когда шаг h на каждой итерации уменьшается не в 2, а в s раз.

Дата добавления: 2014-01-07